Многочлен сложение вычитание умножение многочленов

Приведение подобных членов

Умножение многочлена на число

Умножение одночлена на одночлен

Сложение и вычитание многочленов

Умножение многочлена на многочлен

Приведение подобных членов

Два одночлена называются подобными , если они или равны, или отличаются лишь коэффициентами.

Одночлены, входящие в состав многочлена, часто называют членами многочлена .

Если в многочлен входят подобные одночлены, то желательно совершить операцию приведения подобных членов .

В результате выполнения операции приведения подобных членов подобные одночлены заменяются одним одночленом, коэффициент которого равен алгебраической сумме коэффициентов подобных одночленов.

Покажем, как выполняется операция приведения подобных членов на примере.

Пример 1 . Привести подобные члены в многочлене

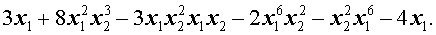
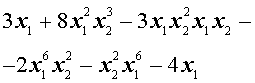
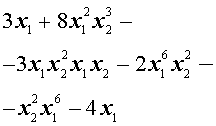
Решение . Преобразуем, если этого не сделано, каждый одночлен, входящий в многочлен, в равный ему одночлен так, чтобы в нём сначала стояла степень буквы x₁ , затем степень буквы x₂ , затем степень буквы x₃ и т.д.:

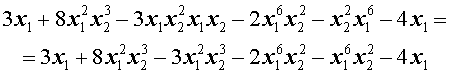
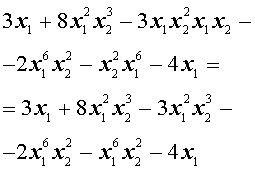
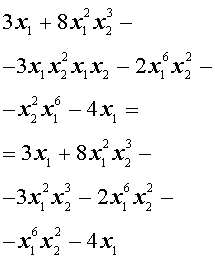
Отметим в полученном многочлене подобные члены одного вида одной чертой сверху, другого вида – двумя чертами сверху, третьего вида – изогнутой линией сверху и т.д.:

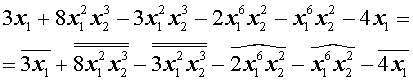
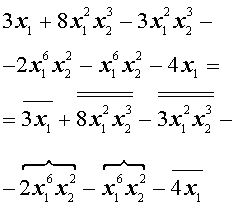
Сгруппируем подобные члены каждого вида и совершим их приведение:

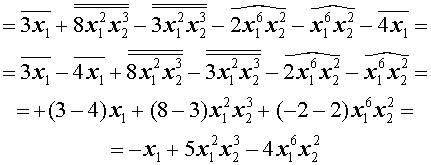
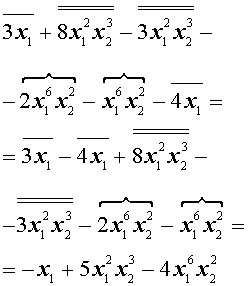
Замечание . Решение примера 1 в учебных целях изложено с подробным и последовательным разбиением на этапы. Конечно же, при наличии опыта (который мы очень рекомендуем приобрести, решая задачи и примеры) приведение подобных членов осуществляется значительно короче и быстрее.

Умножение многочлена на число

При умножении многочлена на число каждый член этого многочлена умножается на это число.

Пример 2 . Выполнить действие

Замечание . Действие в примере 2 называется раскрытием скобки и, конечно же, при наличии даже небольшого опыта выполняется мгновенно.

Умножение одночлена на одночлен

Пример 3 . Выполнить действие

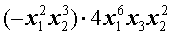
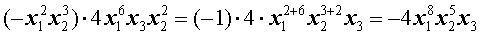
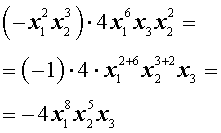
Сложение и вычитание многочленов

Операции сложения и вычитания многочленов близко связаны с операцией приведения подобных членов.

Пример 4 . Выполнить действия

Решение . Раскрывая скобки и приводя подобные члены, получим

Умножение многочлена на многочлен

При умножении многочлена на многочлен каждый член одного многочлена умножается на каждый член другого многочлена, а полученные результаты суммируются.

Заметим, что при умножении двух многочленов, отличных от нуля, получается многочлен, степень которого равна сумме степеней многочленов-сомножителей.

С многочленами можно выполнять следующие действия: сложение, вычитание, умножение, возведение в натуральную степень и деление на ненулевой многочлен. В этой статье мы определим указанные действия с многочленами, то есть, разберемся, как они выполняются и что получается в результате.

Навигация по странице.

Сложение и вычитание

Два первых действия с многочленами – сложение и вычитание – стоит рассматривать вместе, так как они выполняются по одному принципу:

• сначала составляется сумма или разность исходных многочленов, для чего многочлены заключаются в скобки и между этими скобками ставятся знаки плюс или минус;
• после этого раскрываются скобки, в результате получается новый многочлен;
• наконец, при необходимости полученный многочлен приводится к стандартному виду.

Для пояснения приведем решение примера.

Проведите сложение и вычитание многочленов 7·x 2 −1 и x·y−x 2 +2 .

Начнем со сложения. Составим сумму (7·x 2 −1)+(x·y−x 2 +2) . После раскрытия скобок она примет вид 7·x 2 −1+x·y−x 2 +2 . Осталось полученный многочлен привести к стандартному виду: 7·x 2 −1+x·y−x 2 +2=6·x 2 +1+x·y .

Вычитание многочленов проводится аналогично:
(7·x 2 −1)−(x·y−x 2 +2)= 7·x 2 −1−x·y+x 2 −2= 8·x 2 −3−x·y .

(7·x 2 −1)+(x·y−x 2 +2)=6·x 2 +1+x·y и (7·x 2 −1)−(x·y−x 2 +2)=8·x 2 −3−x·y .

Рассмотренные действия более полно освещены в статье сложение и вычитание многочленов.

Умножение

Переходим к следующему действию – умножению многочлена на многочлен. Правило умножения многочлена на многочлен базируется на распределительном свойстве умножения и сводит умножение многочленов к умножению друг на друга всех составляющих их членов, то есть, к умножению одночленов:
чтобы умножить многочлен на многочлен, нужно каждый член первого многочлена умножить на каждый член второго многочлена и сложить полученные произведения.

После выполнения указанных действий будет получен новый многочлен. Иными словами, результатом умножения многочленов является новый многочлен.

Умножьте многочлен a−b на многочлен −3·a+b .

Записываем произведение многочленов: (a−b)·(−3·a+b) . Берем первый член первого многочлена a−b , то есть, a , и умножаем его на каждый член второго многочлена, имеем произведения a·(−3·a) и a·b . Теперь берем второй член первого многочлена, то есть, −b , и умножаем его на все члены второго многочлена, имеем произведения −b·(−3·a) и −b·b . Осталось сложить все полученные произведения: a·(−3·a)+a·b−b·(−3·a)−b·b= −3·a 2 +4·a·b−b 2 .

Покажем, как записывается краткое решение:
(a−b)·(−3·a+b)= a·(−3·a)+a·b−b·(−3·a)−b·b= −3·a 2 +4·a·b−b 2 .

Частным случаем умножения многочленов является умножение многочлена и одночлена.

Рекомендуем продолжить изучение темы, обратившись к статье умножение многочлена на многочлен. Там теория представлена более полно, а также приведены подробные решения типовых примеров.

Возведение многочлена в степень

После того, как мы определили умножение многочленов, можно говорить о возведении многочлена в натуральную степень. Это действие представляет собой умножение исходного многочлена на себя столько раз, сколько указывает показатель степени. Например, возведению многочлена 3·x+1 в четвертую степень соответствует произведение четырех многочленов вида (3·x+1)·(3·x+1)·(3·x+1)·(3·x+1) .

Возведите многочлен 2·a·b−b 3 во вторую степень.

Сначала записываем степень многочлена, дальше переходим к умножению, наконец, выполняем это действие с многочленами:
(2·a·b−b 3 ) 2 =(2·a·b−b 3 )·(2·a·b−b 3 )=
=2·a·b·(2·a·b)+2·a·b·(−b 3 )−b 3 ·(2·a·b)− b 3 ·(−b 3 )= 4·a 2 ·b 2 −4·a·b 4 +b 6 .

(2·a·b−b 3 ) 2 =4·a 2 ·b 2 −4·a·b 4 +b 6 .

В заключение этого пункта стоит отметить, что при возможности для ускорения процесса возведения многочлена в степень можно использовать формулы сокращенного умножения.

Деление

В результате выполнения всех рассмотренных выше действий с многочленами – сложения, вычитания, умножения и возведения в степень, получается многочлен. Деление многочлена на многочлен отличается от указанных действий в том смысле, что в общем случае результат деления не является многочленом. Например, деление многочлена x·y−1 на многочлен x 2 +y 2 дает алгебраическую дробь .

Однако, в частных случаях может получиться и многочлен, например, (x 2 ·y+x·y 2 −x+x·y+y 2 −1):(x+1)=x·y+y 2 −1 . В этих случаях говорят, что один многочлен делится на другой (по аналогии с делимостью целых чисел), а само деление сводится к представлению делимого многочлена в виде произведения делителя и еще одного многочлена, который и является частным от деления. В нашем примере делимое x 2 ·y+x·y 2 −x+x·y+y 2 −1 представляется в виде произведения (x+1)·(x·y+y 2 −1) .

Особое внимание уделяется делению многочленов, содержащих единственную переменную. Пусть задан многочлен с одной действительной переменной x , обозначим его P(x) .

Говорят, что многочлен P(x) делится без остатка (или просто делится) на некоторый многочлен M(x) , если существует многочлен Q(x) такой, что P(x)=M(x)·Q(x) .

Например, многочлен x 3 +2·x 2 +3·x+6 делится на многочлен x+2 , так как существует многочлен x 2 +3 , и справедливо равенство x 3 +2·x 2 +3·x+6=(x+2)·(x 2 +3) . А многочлен x 2 +1 не делится на x 3 −5 без остатка, так как не существует такого многочлена Q(x) , чтобы выполнялось равенство x 2 +1=(x 3 −5)·Q(x) .

Деление многочленов без остатка рассматривается как частный случай деления многочленов с остатком, при котором остаток равен нулю (нулевому многочлену). Вообще, при делении многочлена P(x) степени n ( n≥1 ) на многочлен Q(x) степени k ( 1≤k≤n ) в частном получается некоторый многочлен M(x) степени n−k и многочлен-остаток R(x) , степень которого строго меньше k . Это утверждение можно оформить по аналогии с теоремой о делимости целых чисел.

Любой многочлен P(x) степени n ( n≥1 ) можно представить в виде P(x)=M(x)·Q(x)+R(x) , где Q(x) – некоторый многочлен степени k ( 1≤k≤n ), M(x) – многочлен степени n−k и R(x) – многочлен, степень которого меньше k , причем такое представление единственно (если под Q(x) , M(x) и R(x) понимать любой многочлен из множества тождественно равных им многочленов).

Например, при делении многочлена 3·x 4 +2·x 2 −1 на многочлен x 2 +x получается частное 3·x 2 −3·x+5 и остаток −5·x−1 . Это действительно так, так как справедливо равенство 3·x 4 +2·x 2 −1=(x 2 +x)·(3·x 2 −3·x+5)−5·x−1 , что несложно проверить, выполнив действия с многочленами в его правой части.

При делении многочлена P(x) на многочлен Q(x) , степень которого больше степени делимого многочлена P(x) , частным всегда будет нулевой многочлен, а остаток будет равен делимому многочлену P(x) . Например, при делении x 2 +1 на многочлен x 3 +2·x 2 −1 частым будет 0 , а остатком x 2 +1 .

Деление многочлена на многочлен удобно выполнять уголком, по аналогии с делением чисел. Как выполняется это действие, подробно и на примерах разобрано в статье деление многочлена на многочлен.

При сложении и вычитании многочленов важно уметь использовать правила раскрытия скобок.

Рассмотрим два случая раскрытия скобок:

1. когда перед скобками стоит знак «+»;
2. когда перед скобками стоит знак «−».

Правила раскрытия скобок

Чтобы раскрыть скобки, перед которыми стоит знак « + », нужно просто опустить скобки.

Все знаки у одночленов внутри сохраняются .

Рассмотрим пример. Раскрыть скобки:

3x 2 − 5xy − 7x 2 y + (5xy − 3x 2 + 8x 2 y) = 3x 2 − 5xy − 7x 2 y + 5xy − 3x 2 + 8x 2 y

Чтобы раскрыть скобки, перед которыми стоит знак « − », нужно опустить скобки и заменить все знаки одночленов внутри скобок на противоположные .

Рассмотрим пример. Раскрыть скобки:

7t 3 − 4p − (2t − tn + t) = 7t 3 − 4p − 2t + tn − t

Обратите внимание, так как в этом примере перед скобками стоит знак «−», при раскрытии скобок все одночлены поменяли знаки на противоположные.

Как складывать и вычитать многочлены

Чтобы сложить или вычесть многочлены нужно:

1. раскрыть скобки по правилам раскрытия скобок;
2. максимально привести подобные.

Результат суммы и разности двух многочленов является многочленом.

Рассмотрим пример. Найти разность многочленов.
3a 2 + 8a − 4 и 3 + 8a − 5a 2

Запишем пример. Не забудем заключить весь второй многочлен в скобки.

3a 2 + 8 a − 4 − (3 + 8a − 5a 2 ) = 3a 2 + 8 a − 4 − 3 − 8 a + 5a 2
Теперь подчеркнем и приведем подобные.

3a 2 + 8a − 4 − 3− 8a + 5a 2 = 3a 2 + 5a 2 + 8a − 8a − 4 − 3 = 8a 2 − 7
Запишем окончательное решение.

3a 2 + 8 a − 4 − (3 + 8a − 5a 2 ) = 3a 2 + 8a − 4 − 3− 8a + 5a 2 = 3a 2 + 5a 2 + 8a − 8a − 4 − 3 = 8a 2 − 7

Примеры сложения и вычитания многочленов

1. Найти сумму многочленов 4x − 1 и 5 − 3x
   4x − 1 + (5 − 3x) = 4x − 1 + 5 − 3x = 4x − 3x − 1 + 5 = x + 4

Найти разность многочленов 2с и −b + с
2с − (−b + c) = 2c + b − с = 2с − с + b = с + b

Найти разность многочленов −x 2 и 4ax + x 2
−x 2 − (4ax + x 2 ) = − x 2 − 4ax − x 2 = − x 2 − x 2 −4ax = −2x 2 − 4ax