Содержание
Вершины – точки A, B, и C;
Стороны – отрезки a = BC, b = AC и c = AB, соединяющие вершины;
Углы – α , β, γ образованные тремя парами сторон. Углы часто обозначают так же, как и вершины, – буквами A, B и C.
Угол, образованный сторонами треугольника и лежащий в его внутренней области, называется внутренним углом, а смежный к нему является смежным углом треугольника (2, стр. 534).
Высоты, медианы, биссектрисы и средние линии треугольника
Кроме основных элементов в треугольнике рассматривают и другие отрезки, обладающие интересными свойствами: высоты, медианы, биссектрисы исредние линии.
Высоты треугольника – это перпендикуляры, опущенные из вершин треугольника на противоположные стороны.
Для построения высоты необходимо выполнить следующие действия:
1) провести прямую, содержащую одну из сторон треугольника (в случае, если проводится высота из вершины острого угла в тупоугольном треугольнике);
2) из вершины, лежащей напротив проведенной прямой, провести отрезок из точки к этой прямой, составляющий с ней угол 90 градусов.
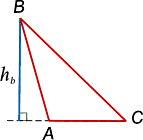
Точка пересечения высоты со стороной треугольника называется основанием высоты (см. рис. 2).
Свойства высот треугольника
В прямоугольном треугольнике высота, проведенная из вершины прямого угла, разбивает его на два треугольника, подобные исходному треугольнику.
В остроугольном треугольнике две его высоты отсекают от него подобные треугольники.
Если треугольник остроугольный, то все основания высот принадлежат сторонам треугольника, а у тупоугольного треугольника две высоты попадают на продолжение сторон.
Три высоты в остроугольном треугольнике пересекаются в одной точке и эту точку называют ортоцентром треугольника.
Медиана
Медианы (от лат. mediana – «средняя») – это отрезки, соединяющие вершины треугольника с серединами противолежащих сторон (см. рис. 3).
Для построения медианы необходимо выполнить следующие действия:
1) найти середину стороны;
2)соединить точку, являющуюся серединой стороны треугольника, с противолежащей вершиной отрезком.
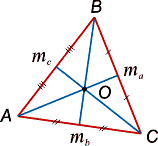
Свойства медиан треугольника
Медиана разбивает треугольник на два треугольника одинаковой площади.
Медианы треугольника пересекаются в одной точке, которая делит каждую из них в отношении 2:1, считая от вершины. Эта точка называется центром тяжести треугольника.
Весь треугольник разделяется своими медианами на шесть равновеликих треугольников.
Биссектриса
Биссектрисами (от лат. bis – дважды» и seko – рассекаю) называют заключенные внутри треугольника отрезки прямых, которые делят пополам его углы (см. рис. 4).
Для построения биссектрисы необходимо выполнить следующие действия:
1) построить луч, выходящий из вершины угла и делящий его на две равные части (биссектрису угла);
2) найти точку пересечения биссектрисы угла треугольника с противоположной стороной;
3) выделить отрезок, соединяющий вершину треугольника с точкой пересечения на противоположной стороне.
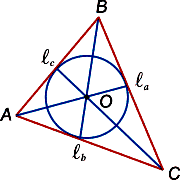
Свойства биссектрис треугольника
Биссектриса угла треугольника делит противоположную сторону в отношении, равном отношению двух прилежащих сторон.
Биссектрисы внутренних углов треугольника пересекаются в одной точке. Это точка называется центром вписанной окружности.
Биссектрисы внутреннего и внешнего углов перпендикулярны.
Если биссектриса внешнего угла треугольника пересекает продолжение противолежащей стороны, то ADBD=ACBC.
Биссектрисы одного внутреннего и двух внешних углов треугольника пересекаются в одной точке. Эта точка — центр одной из трех вневписанных окружностей этого треугольника.
Основания биссектрис двух внутренних и одного внешнего углов треугольника лежат на одной прямой, если биссектриса внешнего угла не параллельна противоположной стороне треугольника.
Если биссектрисы внешних углов треугольника не параллельны противоположным сторонам, то их основания лежат на одной прямой.
Определение
Треугольником называют многоугольник с тремя сторонами и тремя углами. Основными элементами данной геометрической фигуры являются отрезки, вершины и углы. Для решения некоторых задач могут требоваться дополнительные построения.
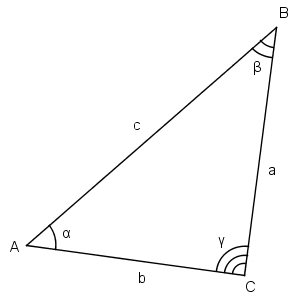
Рис. 1. Основные элементы треугольника.
Рассматриваемое понятие часто обобщают в зависимости от поставленных целей. К примеру, треугольник можно представить тремя точками, которые соединяются между собой отрезками, и не лежат на одной и той же прямой.
С помощью равенства элементов треугольника можно отнести эту геометрическую фигуру к определенному типу. К примеру, если все стороны треугольника равны, то такой треугольник называется равносторонним. С другой стороны, помощь может оказывать и равенство элементов двух треугольников. Так доказывается равенство и подобие фигур.
Общая теория геометрии различных треугольников возникла еще во времена Древней Греции.
Характеристики понятия
Обозначение стороны треугольника традиционно производится по названиям вершин, которые содержит та или иная сторона. По вершинам обозначаются и углы треугольника.
Значение
В общем случае для определения соответствия заданных геометрических фигур используют такие элементы, как:
- две стороны и угол между ними;
- три стороны;
- одну сторону и прилегающие к ней углы.
Когда речь идет о прямоугольных треугольниках, их равенство доказывают с помощью следующих параметров:
- по одинаковым значениям двух катетов;
- используя сопоставление длины катета и гипотенузы;
- сравнивая одного из острых углов и гипотенузы;
- используя сопоставление длины гипотенузы и катета.
Основные свойства главных элементов треугольника касаются его сторон и углов. Более того, нередко требуется построить дополнительный внешний угол, чтобы упростить вычисления других параметров.
Рис. 2. Построение дополнительного внешнего угла.
Треугольники часто рассматривают вместе с их внутренним пространством, что требуется при определении площади геометрической фигуры.
Взаимосвязь основных элементов треугольника
Численную геометрическую характеристику рассматриваемой фигуры на плоскости можно определить, используя определенные данные ее параметров.
Рис. 3. Площадь треугольника на плоскости.
Что мы узнали?
Треугольник состоит из элементов, которые используются в сложных вычислениях. С их помощью можно найти площадь рассматриваемой фигуры, а также доказать ряд теорем.
Тест по теме
Оценка статьи
Средняя оценка: 4.1 . Всего получено оценок: 635.
Не понравилось? — Напиши в комментариях, чего не хватает.
Содержание
- Определение
- Характеристики понятия
- Значение
- Взаимосвязь основных элементов треугольника
- Что мы узнали?
Бонус
-
Тест по теме
- Углы треугольника Элементы треугольника
- Виды углов
По многочисленным просьбам теперь можно: сохранять все свои результаты, получать баллы и участвовать в общем рейтинге.
- 1. Ольга Жаркова 411
- 2. Алина Сайбель 203
- 3. Михаил Тяпин 127
- 4. Денки Каминари 93
- 5. Alex Samin 51
- 6. Елизавета Мельникова 21
- 7. User1 10
- 8. Дмитрий Мантуров 10
- 9. Аркадий Кондюков 9
- 10. Kirra C. 5
- 1. Мария Николаевна 14,295
- 2. Кристина Волосочева 13,830
- 3. Лариса Самодурова 13,785
- 4. Ekaterina 13,631
- 5. Liza 13,310
- 6. Алина Сайбель 13,301
- 7. Юлия Бронникова 13,260
- 8. Darth Vader 12,816
- 9. TorkMen 12,566
- 10. Влад Лубенков 12,025
Самые активные участники недели:
- 1. Виктория Нойманн — подарочная карта книжного магазина на 500 рублей.
- 2. Bulat Sadykov — подарочная карта книжного магазина на 500 рублей.
- 3. Дарья Волкова — подарочная карта книжного магазина на 500 рублей.
Три счастливчика, которые прошли хотя бы 1 тест:
- 1. Наталья Старостина — подарочная карта книжного магазина на 500 рублей.
- 2. Николай З — подарочная карта книжного магазина на 500 рублей.
- 3. Давид Мельников — подарочная карта книжного магазина на 500 рублей.
Карты электронные(код), они будут отправлены в ближайшие дни сообщением Вконтакте или электронным письмом.
Что ты хочешь узнать?
Ответ
Основными элементами треугольника ABC являются:
вершины — точки A , B , и C;
стороны — отрезки a = BC , b = AC и c = AB, соединяющие вершины;
углы , образованные тремя парами сторон. Углы часто обозначают так же, как и вершины, — буквами A , B и C .