$$ int x^2 cos x^3 dx = frac<1> <3>sin x^3 + C $$
Итак, в статье разобрали как решаются некоторые виды интегралов методом занесения под знак дифференциала. Вспомнили дифференциалы часто распространенных элементарных функций. Если не получается или не хватает времени решить задачи контрольных работ самостоятельно, то мы окажем Вам свою помощь в кратчайшие сроки. Достаточно заполнить форму заказа и мы свяжемся с Вами.
При сведении заданного интеграла к табличному часто используются следующие преобразования дифференциала как операция «подведения под знак дифференциала». При этом используется формула:

Вообще говоря, внесение (подведение) под знак дифференциала и замена переменной (метод подстановки) – это один и тот же метод нахождения неопределенного интеграла; отличие состоит только в оформлении.
Суть метода
Итак, внесение под знак интеграла опирается на следующее правило интегрирования. Если в произведении функции, стоящей под знаком интеграла, и дифференциала можно увидеть произведение другой функции и дифференциала от нее, то применяем подведение под знак дифференциала, то есть если

При внесении под знак дифференциала необходимо иметь в виду простейшие преобразования дифференциала:
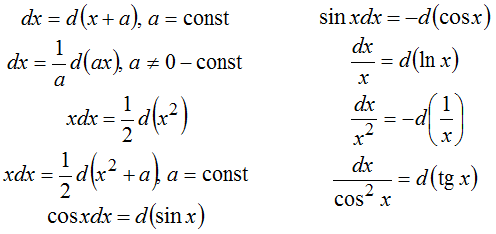
Очень часто метод внесения под знак дифференциала используют для нахождения интегралов вида

Поэтому имеют место следующие формулы для неопределенных интегралов:
Подведение под знак дифференциала решает возникающую при интегрировании проблему, заключающуюся в том, что в подынтегральном выражении находится сложная функция, например,  ,
,  ,
,  и т. п., а под знаком дифференциала d — просто икс. То есть нет возможности сразу применить таблицу интегралов для нахождения такого интеграла.
и т. п., а под знаком дифференциала d — просто икс. То есть нет возможности сразу применить таблицу интегралов для нахождения такого интеграла.
Цель подведения под знак дифференциала — получить простую функцию, которую можно интегрировать непосредственно, то есть по таблице интегралов. Тогда путём преобразований подынтегрального выражения получим простую функцию переменной и эта переменная будет находится и под знаком дифференциала d.
Решение заключается в том, что аргументом подынтегральной функции становится промежуточный аргумент ("внутренняя" функция исходной сложной функции, например,  ,
,  ,
,  и т. п.), который можно обозначить буквой u, и тот же промежуточный аргумент u подводится под знак дифференциала d.
и т. п.), который можно обозначить буквой u, и тот же промежуточный аргумент u подводится под знак дифференциала d.
После того, как такой интеграл будет найден, на место буквы u возвращается обозначаемый ею промежуточный аргумент, и таким образом будет окончательно найден интеграл исходной сложной функции.
Формальная общая запись описанных преобразований выглядит так:
 ,
,
где  — "внешняя" функция, а
— "внешняя" функция, а  — "внутренняя" функция или промежуточный аргумент.
— "внутренняя" функция или промежуточный аргумент.
В примерах вместо буквы u будем использовать букву t: так наши решения будут близки к наглядно понятному методу замены переменной. Кстати, в некоторых источниках метод подведения под знак дифференциала считается частным случаем метода замены переменной.
Повторим: наиболее частый случай, когда выгодно применять подведение под знак дифференциала — подынтегральное выражение представляет собой сложную функцию. Но это не единственный случай, когда требуется применять этот метод интегрирования. Другой распространённый случай — когда нет смысла использовать замену переменной, так как это делает вычисления громоздкими. Тогда, чтобы вычисления были короче, можно использовать подведение под знак дифференциала.
Пример 1. Найти подведением под знак дифференциала интеграл:
 .
.
Решение. Внесём под знак дифференциала внутреннюю функцию. Это почти то же самое, что найти её производную. Получаем
 .
.
Полученное нужно перенести в подынтегральное выражение, но в нём нет множителя-тройки перед дифференциалом. Значит, перед знаком интеграла ставим 1/3 и получаем:
 .
.
Далее для получения простой функции обозначаем  и
и  и окончательно решаем как табличный интеграл 7:
и окончательно решаем как табличный интеграл 7:

Пример 2. Найти подведением под знак дифференциала интеграл:
 .
.
Решение. Сразу же видим, что дифференциал синуса от икса равен косинусу от икса, а это как раз то, что нам нужно. Внесём под знак дифференциала синус от икса. Получаем
 .
.
Полученное переносим в подынтегральное выражение:
 .
.
Далее для получения простой функции обозначаем  и
и  и окончательно решаем как табличный интеграл 7:
и окончательно решаем как табличный интеграл 7:
 .
.
Пример 3. Найти подведением под знак дифференциала интеграл:
 .
.
Решение. Внесём под знак дифференциала внутреннюю функцию. Получаем
 .
.
Полученное нужно перенести в подынтегральное выражение, но в нём нет множителя-двойки перед дифференциалом. Значит, перед знаком интеграла ставим 1/2 и получаем:

Далее для получения простой функции обозначаем  и
и  и окончательно решаем как табличный интеграл 7:
и окончательно решаем как табличный интеграл 7:
 .
.
Применить подведение под знак дифференциала самостоятельно, а затем посмотреть решение
Следующие задачи — общий случай: решаются по определению дифференциала функции:
 .
.
Пример 4. Найти подведением под знак дифференциала интеграл:
 .
.
Пример 5. Найти подведением под знак дифференциала интеграл:
 .
.
В следующих задачах используются правила дифференцирования и интегрирования констант:
Так как  , то
, то  , иными словами, константу можно подвести под знак дифференциала.
, иными словами, константу можно подвести под знак дифференциала.
Пример 6. Найти подведением под знак дифференциала интеграл:
 .
.
Так как  , где C — произвольная константа, то
, где C — произвольная константа, то  .
.
Пример 7. Найти подведением под знак дифференциала интеграл:
 .
.
Пример 8. Найти подведением под знак дифференциала интеграл:
 .
.
Решение. Внесём под знак дифференциала внутреннюю функцию — минус икс в квадрате. Получаем
 .
.
Полученное нужно перенести в подынтегральное выражение, но в нём нет множителя-минус двух перед дифференциалом. Значит, перед знаком интеграла ставим -1/2 и получаем:
 .
.
Далее для получения простой функции обозначаем  и
и  и окончательно решаем как табличный интеграл 11:
и окончательно решаем как табличный интеграл 11:

Пример 9. Найти подведением под знак дифференциала интеграл:
 .
.
Решение. Внесём под знак дифференциала внутреннюю функцию — логарифм икса. Получаем
 .
.
Полученное нужно перенести в подынтегральное выражение:
 .
.
Далее для получения простой функции обозначаем  и
и  и окончательно решаем как табличный интеграл 12:
и окончательно решаем как табличный интеграл 12:
 .
.
Пример 10. Найти подведением под знак дифференциала интеграл:
 .
.
Решение. Внесём под знак дифференциала внутреннюю функцию — ту, что в знаменателе. Получаем
 .
.
Полученное нужно перенести в подынтегральное выражение, но в нём нет множителя-минус трёх перед дифференциалом. Значит, перед знаком интеграла ставим -1/3 и получаем:
 .
.
Далее для получения простой функции обозначаем  и
и  и окончательно решаем как табличный интеграл 10:
и окончательно решаем как табличный интеграл 10:
 .
.
Пример 11. Найти подведением под знак дифференциала интеграл:
 .
.
Решение. Замечаем, что замена переменной в знаменателе выгодно оборачивается получением табличного интеграла 21 (с арктангенсом). Но в знаменателе у нас икс не в квадрате, а в шестой степени. Представляем икс в шестой степени как  , а интеграл преобразуется к
, а интеграл преобразуется к  . Именно икс в кубе из второго слагаемого в знаменателе представляет собой внутреннюю функцию, которую внесём под знак дифференциала. Получаем
. Именно икс в кубе из второго слагаемого в знаменателе представляет собой внутреннюю функцию, которую внесём под знак дифференциала. Получаем
 .
.
Полученное нужно перенести в подынтегральное выражение. В нём нет множителя-тройки перед дифференциалом. Значит, перед знаком интеграла ставим 1/3 и получаем:
 .
.
Далее для получения простой функции обозначаем  и
и  и окончательно решаем как табличный интеграл 21:
и окончательно решаем как табличный интеграл 21:
 .
.
Пример 12. Найти подведением под знак дифференциала интеграл:
 .
.
Решение. Смотрим в числитель. Там косинус от трёх икс. Смотрим в знаменатель. Там присутствует синус также от трёх икс. Значит, всё выражение в знаменателе можем как внутреннюю функцию внести под знак дифференциала. Получаем
 .
.
Полученное нужно перенести в подынтегральное выражение. В нём нет множителя-минус девяти перед дифференциалом. Значит, перед знаком интеграла ставим -1/9 и получаем:
 .
.
Далее для получения простой функции обозначаем  и
и  и окончательно решаем как табличный интеграл 10:
и окончательно решаем как табличный интеграл 10:



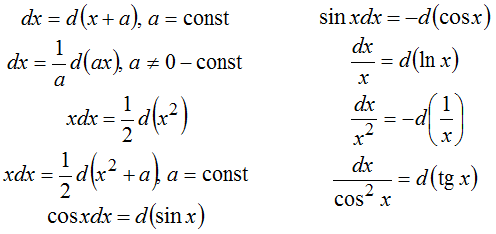

 ,
,  ,
,  и т. п., а под знаком дифференциала d — просто икс. То есть нет возможности сразу применить таблицу интегралов для нахождения такого интеграла.
и т. п., а под знаком дифференциала d — просто икс. То есть нет возможности сразу применить таблицу интегралов для нахождения такого интеграла. ,
,  ,
,  и т. п.), который можно обозначить буквой u, и тот же промежуточный аргумент u подводится под знак дифференциала d.
и т. п.), который можно обозначить буквой u, и тот же промежуточный аргумент u подводится под знак дифференциала d. ,
, — "внешняя" функция, а
— "внешняя" функция, а  — "внутренняя" функция или промежуточный аргумент.
— "внутренняя" функция или промежуточный аргумент. .
. .
. .
. и
и  и окончательно решаем как табличный интеграл 7:
и окончательно решаем как табличный интеграл 7:
 .
. .
. .
. и
и  и окончательно решаем как табличный интеграл 7:
и окончательно решаем как табличный интеграл 7: .
. .
. .
.
 и
и  и окончательно решаем как табличный интеграл 7:
и окончательно решаем как табличный интеграл 7: .
. .
. .
. .
. , то
, то  , иными словами, константу можно подвести под знак дифференциала.
, иными словами, константу можно подвести под знак дифференциала. .
. , где C — произвольная константа, то
, где C — произвольная константа, то  .
. .
. .
. .
. .
. и
и  и окончательно решаем как табличный интеграл 11:
и окончательно решаем как табличный интеграл 11:
 .
. .
. .
. и
и  и окончательно решаем как табличный интеграл 12:
и окончательно решаем как табличный интеграл 12: .
. .
. .
. .
. и
и  и окончательно решаем как табличный интеграл 10:
и окончательно решаем как табличный интеграл 10: .
. .
. , а интеграл преобразуется к
, а интеграл преобразуется к  . Именно икс в кубе из второго слагаемого в знаменателе представляет собой внутреннюю функцию, которую внесём под знак дифференциала. Получаем
. Именно икс в кубе из второго слагаемого в знаменателе представляет собой внутреннюю функцию, которую внесём под знак дифференциала. Получаем .
. .
. и
и  и окончательно решаем как табличный интеграл 21:
и окончательно решаем как табличный интеграл 21: .
. .
. .
. .
. и
и  и окончательно решаем как табличный интеграл 10:
и окончательно решаем как табличный интеграл 10: