Тетраэдр помещен в прямоугольную систему координат

Содержание

Страница № 497.

Учебник: Задачи к урокам геометрии. 7-11 классы. Зив Б.Г. — С.-Петербург, 1998. НПО «Мир и семья-95» — 624 с.: ил.

1. Тетраэдр DABC помещен в прямоугольную систему координат (рис. 4). LACD- 90°; АВ — 8; /.ВАС — 60°. DB± ABC; плоскость ADC составляет с плоскостью ABC угол 60°.

1) Найдите координаты вершин тетраэдра.

2^ Найдите координаты вектора АК, где К — точка пересечения медиан грани DBC, и разложите этот вектор по векторам и 7*и 1с.

2. В пространстве д^ны точки А, В и^ С, причем АВ <2; 3; — 1>и АС <— 4; т; п>. При каких т и п эти точки лежат на одной прямой?

1. Тетраэдр DABC помещен в прямоугольную систему координат (рис. 5) АВ = АС

25; ВС = 30; ВО = ОС. Грань A DC составляет с плоскостью основания угол 45°.

1) Найдите координаты вершин тетраэдра.

2) Найдите координаты вектора ОК, где К — основание перпендикуляра, опущенного из точки О на грань ACD, и разложите этот вектор по

2. При каких значениях т векторы а <2; — 1; 3>, 3? <1; 3; —2>ис(т; 2; 1> компланарны?

Учебник: Задачи к урокам геометрии. 7-11 классы. Зив Б.Г. — С.-Петербург, 1998. НПО «Мир и семья-95» — 624 с.: ил.

Метод координат — это, конечно, очень хорошо, но в настоящих задачах C2 никаких координат и векторов нет. Поэтому их придется вводить. Да-да, вот так взять и ввести: указать начало отсчета, единичный отрезок и направление осей x, y и z.

Самое замечательное свойство этого метода заключается в том, что не имеет никакого значения, как именно вводить систему координат. Если все вычисления будут правильными, то и ответ будет правильным.

Тем не менее, приведу некоторые рекомендации, как лучше ввести систему координат для самых часто встречающихся в задаче C2 многогранников. С указанием конкретных точек. Во всех случаях упор делается на минимизацию объема вычислений.

Координаты куба

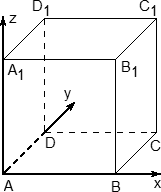
Если в задаче C2 будет куб — считайте, что вам повезло. Это самый простой многогранник, все двугранные углы которого равны 90°.

Система координат также вводится очень просто:

Начало координат — в точке A;
Чаще всего ребро куба не указано, поэтому принимаем его за единичный отрезок;
Ось x направляем по ребру AB, y — по ребру AD, а ось z — по ребру AA₁.

Обратите внимание: ось z направляется вверх! После двумерной системы координат это несколько непривычно, но на самом деле очень логично.

Итак, теперь у каждой вершины куба есть координаты. Соберем их в таблицу — отдельно для нижней плоскости куба:

Точка	A	B	C	D
Координаты	(0; 0; 0)	(1; 0; 0)	(1; 1; 0)	(0; 1; 0)

Точка	A₁	B₁	C₁	D₁
Координаты	(0; 0; 1)	(1; 0; 1)	(1; 1; 1)	(0; 1; 1)

Несложно заметить, что точки верхней плоскости отличаются соответствующих точек нижней только координатой z. Например, B = (1; 0; 0), B₁ = (1; 0; 1). Главное — не запутаться!

Координаты трехгранной призмы

Призма — это уже намного веселее. При правильном подходе достаточно знать координаты только нижнего основания — верхнее будет считаться автоматически.

В задачах C2 встречаются исключительно правильные трехгранные призмы (прямые призмы, в основании которых лежит правильный треугольник). Для них система координат вводится почти так же, как и для куба. Кстати, если кто не в курсе, куб — это тоже призма, только четырехгранная.

Итак, поехали! Вводим систему координат:

Начало координат — в точке A;
Сторону призмы принимаем за единичный отрезок, если иное не указано в условии задачи;
Ось x направляем по ребру AB, z — по ребру AA₁, а ось y расположим так, чтобы плоскость OXY совпадала с плоскостью основания ABC.

Здесь требуются некоторые пояснения. Дело в том, что ось y НЕ совпадает с ребром AC, как многие считают. А почему не совпадает? Подумайте сами: треугольник ABC — равносторонний, в нем все углы по 60°. А углы между осями координат должны быть по 90°, поэтому сверху картинка будет выглядеть так:

Надеюсь, теперь понятно, почему ось y не пойдет вдоль AC. Проведем в этом треугольнике высоту CH. Треугольник ACH — прямоугольный, причем AC = 1, поэтому AH = 1 · cos A = cos 60°; CH = 1 · sin A = sin 60°. Эти факты нужны для вычисления координат точки C.

Теперь взглянем на всю призму вместе с построенной системой координат:

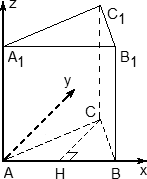
Получаем следующие координаты точек:

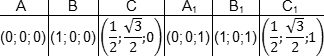
Как видим, точки верхнего основания призмы снова отличаются от соответствующих точек нижнего лишь координатой z. Основная проблема — это точки C и C₁. У них есть иррациональные координаты, которые надо просто запомнить. Ну, или понять, откуда они возникают.

Координаты шестигранной призмы

Шестигранная призма — это «клонированная» трехгранная. Можно понять, как это происходит, если взглянуть на нижнее основание — обозначим его ABCDEF. Проведем дополнительные построения: отрезки AD, BE и CF. Получилось шесть треугольников, каждый из которых (например, треугольник ABO) является основанием для трехгранной призмы.

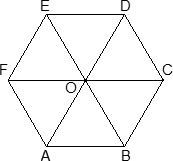
Теперь введем собственно систему координат. Начало координат — точку O — поместим в центр симметрии шестиугольника ABCDEF. Ось x пойдет вдоль FC, а ось y — через середины отрезков AB и DE. Получим такую картинку:

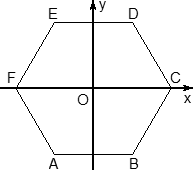
Обратите внимание: начало координат НЕ совпадает с вершиной многогранника! На самом деле, при решении настоящих задач вы обнаружите, что это очень удобно, поскольку позволяет значительно уменьшить объем вычислений.

Осталось добавить ось z. По традиции, проводим ее перпендикулярно плоскости OXY и направляем вертикально вверх. Получим итоговую картинку:

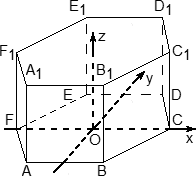
Запишем теперь координаты точек. Предположим, что все ребра нашей правильной шестигранной призмы равны 1. Итак, координаты нижнего основания:

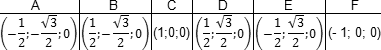
Координаты верхнего основания сдвинуты на единицу по оси z:

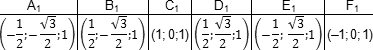
Координаты четырехугольной пирамиды

Пирамида — это вообще очень сурово. Мы разберем только самый простой случай — правильную четырехугольную пирамиду, все ребра которой равны единице. Однако в настоящих задачах C2 длины ребер могут отличаться, поэтому ниже приведена и общая схема вычисления координат.

Итак, правильная четырехугольная пирамида. Это такая же, как у Хеопса, только чуть поменьше. Обозначим ее SABCD, где S — вершина. Введем систему координат: начало в точке A, единичный отрезок AB = 1, ось x направим вдоль AB, ось y — вдоль AD, а ось z — вверх, перпендикулярно плоскости OXY. Для дальнейших вычислений нам потребуется высота SH — вот и построим ее. Получим следующую картинку:

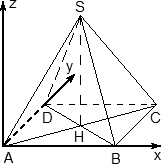
Теперь найдем координаты точек. Для начала рассмотрим плоскость OXY. Здесь все просто: в основании лежит квадрат, его координаты известны. Проблемы возникают с точкой S. Поскольку SH — высота к плоскости OXY, точки S и H отличаются лишь координатой z. Собственно, длина отрезка SH — это и есть координата z для точки S, поскольку H = (0,5; 0,5; 0).

Заметим, что треугольники ABC и ASC равны по трем сторонам (AS = CS = AB = CB = 1, а сторона AC — общая). Следовательно, SH = BH. Но BH — половина диагонали квадрата ABCD, т.е. BH = AB · sin 45°. Получаем координаты всех точек:

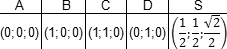
Вот и все с координатами пирамиды. Но не с координатами вообще. Мы рассмотрели лишь самые распространенные многогранники, однако этих примеров достаточно, чтобы самостоятельно вычислить координаты любых других фигур. Поэтому можно приступать, собственно, к методам решения конкретных задач C2.

Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7

Задача 2: Дана окружность радиуса r и на ней точка А. Найти множество точек , делящих всевозможные хорды, проведенные через точку А, в одном и том же отношении , где .

Решение. Возьмем прямоугольную систему координат так, чтобы центр данной окружности совпал с началом координат, а точка А имела координаты (рис. 20).

Пусть АВ — произвольная хорда, проходящая через точку А, а М — точка, множества , т. е. . Обозначив координаты точек В и М соответственно через и (х; у), будем иметь: .

Отсюда, учитывая, что , получаем:

Так как точка лежит на данной окружности, то , поэтому

или

Итак, доказано, что если М(х; у) — произвольная точка искомого множества , то ее координаты удовлетворяют последнему уравнению. Обратно, если координаты (х; у) точки М удовлетворяют последнему уравнению, то они удовлетворяют также уравнению:

Отсюда следует, что точка , координаты которой определяются равенствами: , лежит на данной окружности . С другой стороны, из равенств: получаем равенства: , т. е. точка М делит отрезок АВ в отношении и, следовательно, .

Таким образом, множество определяется уравнением:

т. е. является окружностью радиуса (без точки А) с центром в точке . Эта окружность при любом проходит через точку А. При = 1 одним из диаметров окружности является отрезок АО.

Читайте также: Ссп 99м или сева

Задачи для аудиторной работы:

1. Найти множество всех точек плоскости, для каждой из которых разность квадратов расстояний от двух данных точек A и В есть постоянная величина c.

2. Найти множество всех точек, для каждой из которых отношение расстояний от двух данных точек А и В есть постоянная величина , не равная единице.

3. Лестница, стоящая на гладком полу у стены, соскальзывает вниз. По какой линии движется котенок, сидящий на середине лестницы?

4. Два наблюдаемых пункта находится и точках и . Пункт наблюдения О находится на прямой АВ и удален от точки А на расстояние а км, а от В на расстояние с км (с > а). Наблюдатель для безопасности должен идти по такому пути, чтобы расстояние от него до пункта А все время оставалось в два раза больше, чем расстояние от него до пункта В. По какой линии должен идти наблюдатель?

5. Два предприятия А и В производят продукцию с одной и той же ценой m за одно изделие. Однако автопарк, обслуживающий предприятие A, оснащен более современными и более мощными грузовыми автомобилями. В результате транспортные расходы на перевозку одного изделия составляют для предприятия А 10 к. на 1 км, а для предприятия В 20 к. на 1 км. Расстояние между предприятиями 300 км. Как территориально должен быть разделен рынок сбыта между двумя предприятиями для того, чтобы расходы потребителей при покупке изделий были минимальными?

8. векторный метод

В курсе элементарной математики выделяются два типа задач, решаемых с помощью векторного метода:

I тип – задачи, связанные с использованием операций сложения векторов и умножения вектора на число;

II тип – задачи с использованием операций скалярного умножения векторов и разложения вектора по базису.

Второй тип задач имеет следующий алгоритм решения:

1. Выбираем базисные векторы (наиболее удобные для работы). Обычно, в качестве базисных векторов выбирают векторы, имеющие равные длины, с известной мерой угла между этими векторами.

2. Раскладываем «ключевой» вектор по базисным векторам.

3. Исходя из условия задачи, составляем, если необходимо, систему, связывающую неизвестные коэффициенты разложения «ключевого» вектора по базису.

4. Проверяем, что полученные числовые значения для коэффициентов удовлетворяют наложенным на них условиям.

5. Ответ записываем в безвекторной форме.

При решении геометрических задач векторным методом следует помнить важные эвристики, представленные в разделе «Справочник».

Следующие примеры иллюстрируют векторный метод.

Задача 1: На сторонах АВ и АС треугольника АВС заданы точки М и N, такие, что и . Отрезки ВN и СМ пересекаются в точке K. В каком отношении точка К делит каждый из этих отрезков?