Степень делим на степень

Содержание

Как делить степени? При каких условиях деление степеней возможно?

В алгебре найти частное степеней можно в двух случаях:

1) если степени имеют одинаковые основания;

2) если степени имеют одинаковые показатели.

Чтобы разделить степени с одинаковыми основаниями, надо основание оставить прежним, а из показателя степени делимого вычесть показатель степени делителя (или коротко: при делении степеней показатели вычитают):

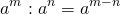
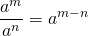
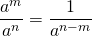
(последнюю формулу удобно использовать, если показатель степени в знаменателе больше показателя степени в числителе).

При делении степеней с одинаковыми показателями общий показатель можно вынести за скобки:

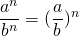
Рассмотрим, как делить степени, на конкретных примерах.

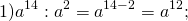
Единицу в показателе степени не пишут, но при делении степеней ее следует учесть:

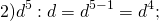
При делении степеней с одинаковыми основаниями и одинаковыми показателями получаем единицу:

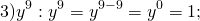
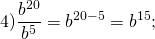
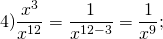
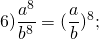
Вынесение общего показателя при делении степеней позволяет упростить вычисления:

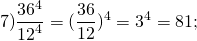
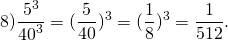
В выражениях возведение в степень выполняется в первую очередь.

Если нужно число разделить на степень либо степень разделить на число, сначала следует выполнить возведение в степень, а затем — деление:

Рассмотрим тему преобразования выражений со степенями, но прежде остановимся на ряде преобразований, которые можно проводить с любыми выражениями, в том числе со степенными. Мы научимся раскрывать скобки, приводить подобные слагаемые, работать с основанием и показателем степени, использовать свойства степеней.

Что представляют собой степенные выражения?

В школьном курсе мало кто использует словосочетание «степенные выражения», зато этот термин постоянно встречается в сборниках для подготовки к ЕГЭ. В большинства случаев словосочетанием обозначаются выражения, которые содержат в своих записях степени. Это мы и отразим в нашем определении.

Степенное выражение – это выражение, которое содержит степени.

Приведем несколько примеров степенных выражений, начиная со степени с натуральным показателем и заканчивая степенью с действительным показателем.

Самыми простыми степенными выражениями можно считать степени числа с натуральным показателем: 3 2 , 7 5 + 1 , ( 2 + 1 ) 5 , ( − 0 , 1 ) 4 , 2 2 3 3 , 3 · a 2 − a + a 2 , x 3 − 1 , ( a 2 ) 3 . А также степени с нулевым показателем: 5 0 , ( a + 1 ) 0 , 3 + 5 2 − 3 , 2 0 . И степени с целыми отрицательными степенями: ( 0 , 5 ) 2 + ( 0 , 5 ) — 2 2 .

Чуть сложнее работать со степенью, имеющей рациональный и иррациональный показатели: 264 1 4 — 3 · 3 · 3 1 2 , 2 3 , 5 · 2 — 2 2 — 1 , 5 , 1 a 1 4 · a 1 2 — 2 · a — 1 6 · b 1 2 , x π · x 1 — π , 2 3 3 + 5 .

В качестве показателя может выступать переменная 3 x — 54 — 7 · 3 x — 58 или логарифм x 2 · l g x − 5 · x l g x .

С вопросом о том, что такое степенные выражения, мы разобрались. Теперь займемся их преобразованием.

Основные виды преобразований степенных выражений

В первую очередь мы рассмотрим основные тождественные преобразования выражений, которые можно выполнять со степенными выражениями.

Вычислите значение степенного выражения 2 3 · ( 4 2 − 12 ) .

Решение

Все преобразования мы будем проводить с соблюдением порядка выполнения действий. В данном случае начнем мы с выполнения действий в скобках: заменим степень на цифровое значение и вычислим разность двух чисел. Имеем 2 3 · ( 4 2 − 12 ) = 2 3 · ( 16 − 12 ) = 2 3 · 4 .

Нам остается заменить степень 2 3 ее значением 8 и вычислить произведение 8 · 4 = 32 . Вот наш ответ.

Ответ: 2 3 · ( 4 2 − 12 ) = 32 .

Упростите выражение со степенями 3 · a 4 · b − 7 − 1 + 2 · a 4 · b − 7 .

Решение

Данное нам в условии задачи выражение содержит подобные слагаемые, которые мы можем привести: 3 · a 4 · b − 7 − 1 + 2 · a 4 · b − 7 = 5 · a 4 · b − 7 − 1 .

Ответ: 3 · a 4 · b − 7 − 1 + 2 · a 4 · b − 7 = 5 · a 4 · b − 7 − 1 .

Представьте выражение со степенями 9 — b 3 · π — 1 2 в виде произведения.

Решение

Представим число 9 как степень 3 2 и применим формулу сокращенного умножения:

9 — b 3 · π — 1 2 = 3 2 — b 3 · π — 1 2 = = 3 — b 3 · π — 1 3 + b 3 · π — 1

Ответ: 9 — b 3 · π — 1 2 = 3 — b 3 · π — 1 3 + b 3 · π — 1 .

А теперь перейдем к разбору тождественных преобразований, которые могут применяться именно в отношении степенных выражений.

Работа с основанием и показателем степени

Степень в основании или показателе может иметь и числа, и переменные, и некоторые выражения. Например, ( 2 + 0 , 3 · 7 ) 5 − 3 , 7 и ( a · ( a + 1 ) − a 2 ) 2 · ( x + 1 ) . Работать с такими записями сложно. Намного проще заменить выражение в основании степени или выражение в показателе тождественно равным выражением.

Проводятся преобразования степени и показателя по известным нам правилам отдельно друг от друга. Самое главное, чтобы в результате преобразований получилось выражение, тождественное исходному.

Читайте также: Самый дешевый чпу станок

Цель преобразований – упростить исходное выражение или получить решение задачи. Например, в примере, который мы привели выше, ( 2 + 0 , 3 · 7 ) 5 − 3 , 7 можно выполнить действия для перехода к степени 4 , 1 1 , 3 . Раскрыв скобки, мы можем привести подобные слагаемые в основании степени ( a · ( a + 1 ) − a 2 ) 2 · ( x + 1 ) и получить степенное выражение более простого вида a 2 · ( x + 1 ) .

Использование свойств степеней

Свойства степеней, записанные в виде равенств, являются одним из главных инструментов преобразования выражений со степенями. Приведем здесь основные из них, учитывая, что a и b – это любые положительные числа, а r и s — произвольные действительные числа:

a r · a s = a r + s ;
a r : a s = a r − s ;
( a · b ) r = a r · b r ;
( a : b ) r = a r : b r ;
( a r ) s = a r · s .

В тех случаях, когда мы имеем дело с натуральными, целыми, положительными показателями степени, ограничения на числа a и b могут быть гораздо менее строгими. Так, например, если рассмотреть равенство a m · a n = a m + n , где m и n – натуральные числа, то оно будет верно для любых значений a , как положительных, так и отрицательных, а также для a = 0 .

Применять свойства степеней без ограничений можно в тех случаях, когда основания степеней положительные или содержат переменные, область допустимых значений которых такова, что на ней основания принимают лишь положительные значения. Фактически, в рамках школьной программы по математике задачей учащегося является выбор подходящего свойства и правильное его применение.

При подготовке к поступлению в Вузы могут встречаться задачи, в которых неаккуратное применение свойств будет приводить к сужению ОДЗ и другим сложностям с решением. В данном разделе мы разберем всего два таких случая. Больше информации по вопросу можно найти в теме «Преобразование выражений с использованием свойств степеней».

Представьте выражение a 2 , 5 · ( a 2 ) − 3 : a − 5 , 5 в виде степени с основанием a .

Решение

Для начала используем свойство возведения в степень и преобразуем по нему второй множитель ( a 2 ) − 3 . Затем используем свойства умножения и деления степеней с одинаковым основанием:

a 2 , 5 · a − 6 : a − 5 , 5 = a 2 , 5 − 6 : a − 5 , 5 = a − 3 , 5 : a − 5 , 5 = a − 3 , 5 − ( − 5 , 5 ) = a 2 .

Ответ: a 2 , 5 · ( a 2 ) − 3 : a − 5 , 5 = a 2 .

Преобразование степенных выражений согласно свойству степеней может производиться как слева направо, так и в обратном направлении.

Найти значение степенного выражения 3 1 3 · 7 1 3 · 21 2 3 .

Решение

Если мы применим равенство ( a · b ) r = a r · b r , справа налево, то получим произведение вида 3 · 7 1 3 · 21 2 3 и дальше 21 1 3 · 21 2 3 . Сложим показатели при умножении степеней с одинаковыми основаниями: 21 1 3 · 21 2 3 = 21 1 3 + 2 3 = 21 1 = 21 .

Есть еще один способ провести преобразования:

3 1 3 · 7 1 3 · 21 2 3 = 3 1 3 · 7 1 3 · ( 3 · 7 ) 2 3 = 3 1 3 · 7 1 3 · 3 2 3 · 7 2 3 = = 3 1 3 · 3 2 3 · 7 1 3 · 7 2 3 = 3 1 3 + 2 3 · 7 1 3 + 2 3 = 3 1 · 7 1 = 21

Ответ: 3 1 3 · 7 1 3 · 21 2 3 = 3 1 · 7 1 = 21

Дано степенное выражение a 1 , 5 − a 0 , 5 − 6 , введите новую переменную t = a 0 , 5 .

Решение

Представим степень a 1 , 5 как a 0 , 5 · 3 . Используем свойство степени в степени ( a r ) s = a r · s справа налево и получим ( a 0 , 5 ) 3 : a 1 , 5 − a 0 , 5 − 6 = ( a 0 , 5 ) 3 − a 0 , 5 − 6 . В полученное выражение можно без проблем вводить новую переменную t = a 0 , 5 : получаем t 3 − t − 6 .

Ответ: t 3 − t − 6 .

Преобразование дробей, содержащих степени

Обычно мы имеем дело с двумя вариантами степенных выражений с дробями: выражение представляет собой дробь со степенью или содержит такую дробь. К таким выражениям применимы все основные преобразования дробей без ограничений. Их можно сокращать, приводить к новому знаменателю, работать отдельно с числителем и знаменателем. Проиллюстрируем это примерами.

Упростить степенное выражение 3 · 5 2 3 · 5 1 3 — 5 — 2 3 1 + 2 · x 2 — 3 — 3 · x 2 .

Решение

Мы имеем дело с дробью, поэтому проведем преобразования и в числителе, и в знаменателе:

3 · 5 2 3 · 5 1 3 — 5 — 2 3 1 + 2 · x 2 — 3 — 3 · x 2 = 3 · 5 2 3 · 5 1 3 — 3 · 5 2 3 · 5 — 2 3 — 2 — x 2 = = 3 · 5 2 3 + 1 3 — 3 · 5 2 3 + — 2 3 — 2 — x 2 = 3 · 5 1 — 3 · 5 0 — 2 — x 2

Поместим минус перед дробью для того, чтобы изменить знак знаменателя: 12 — 2 — x 2 = — 12 2 + x 2

Ответ: 3 · 5 2 3 · 5 1 3 — 5 — 2 3 1 + 2 · x 2 — 3 — 3 · x 2 = — 12 2 + x 2

Дроби, содержащие степени, приводятся к новому знаменателю точно также, как и рациональные дроби. Для этого необходимо найти дополнительный множитель и умножить на него числитель и знаменатель дроби. Подбирать дополнительный множитель необходимо таким образом, чтобы он не обращался в нуль ни при каких значениях переменных из ОДЗ переменных для исходного выражения.

Приведите дроби к новому знаменателю: а) a + 1 a 0 , 7 к знаменателю a , б) 1 x 2 3 — 2 · x 1 3 · y 1 6 + 4 · y 1 3 к знаменателю x + 8 · y 1 2 .

Решение

а) Подберем множитель, который позволит нам произвести приведение к новому знаменателю. a 0 , 7 · a 0 , 3 = a 0 , 7 + 0 , 3 = a , следовательно, в качестве дополнительного множителя мы возьмем a 0 , 3 . Область допустимых значений переменной а включает множество всех положительных действительных чисел. В этой области степень a 0 , 3 не обращается в нуль.

Выполним умножение числителя и знаменателя дроби на a 0 , 3 :

a + 1 a 0 , 7 = a + 1 · a 0 , 3 a 0 , 7 · a 0 , 3 = a + 1 · a 0 , 3 a

б) Обратим внимание на знаменатель:

x 2 3 — 2 · x 1 3 · y 1 6 + 4 · y 1 3 = = x 1 3 2 — x 1 3 · 2 · y 1 6 + 2 · y 1 6 2

Умножим это выражение на x 1 3 + 2 · y 1 6 , получим сумму кубов x 1 3 и 2 · y 1 6 , т.е. x + 8 · y 1 2 . Это наш новый знаменатель, к которому нам надо привести исходную дробь.

Так мы нашли дополнительный множитель x 1 3 + 2 · y 1 6 . На области допустимых значений переменных x и y выражение x 1 3 + 2 · y 1 6 не обращается в нуль, поэтому, мы можем умножить на него числитель и знаменатель дроби:
1 x 2 3 — 2 · x 1 3 · y 1 6 + 4 · y 1 3 = = x 1 3 + 2 · y 1 6 x 1 3 + 2 · y 1 6 x 2 3 — 2 · x 1 3 · y 1 6 + 4 · y 1 3 = = x 1 3 + 2 · y 1 6 x 1 3 3 + 2 · y 1 6 3 = x 1 3 + 2 · y 1 6 x + 8 · y 1 2

Ответ: а) a + 1 a 0 , 7 = a + 1 · a 0 , 3 a , б) 1 x 2 3 — 2 · x 1 3 · y 1 6 + 4 · y 1 3 = x 1 3 + 2 · y 1 6 x + 8 · y 1 2 .

Сократите дробь: а) 30 · x 3 · ( x 0 , 5 + 1 ) · x + 2 · x 1 1 3 — 5 3 45 · x 0 , 5 + 1 2 · x + 2 · x 1 1 3 — 5 3 , б) a 1 4 — b 1 4 a 1 2 — b 1 2 .

Решение

а) Используем наибольший общий знаменатель (НОД), на который можно сократить числитель и знаменатель. Для чисел 30 и 45 это 15 . Также мы можем произвести сокращение на x 0 , 5 + 1 и на x + 2 · x 1 1 3 — 5 3 .

30 · x 3 · ( x 0 , 5 + 1 ) · x + 2 · x 1 1 3 — 5 3 45 · x 0 , 5 + 1 2 · x + 2 · x 1 1 3 — 5 3 = 2 · x 3 3 · ( x 0 , 5 + 1 )

б) Здесь наличие одинаковых множителей неочевидно. Придется выполнить некоторые преобразования для того, чтобы получить одинаковые множители в числителе и знаменателе. Для этого разложим знаменатель, используя формулу разности квадратов:

a 1 4 — b 1 4 a 1 2 — b 1 2 = a 1 4 — b 1 4 a 1 4 2 — b 1 2 2 = = a 1 4 — b 1 4 a 1 4 + b 1 4 · a 1 4 — b 1 4 = 1 a 1 4 + b 1 4

Ответ: а) 30 · x 3 · ( x 0 , 5 + 1 ) · x + 2 · x 1 1 3 — 5 3 45 · x 0 , 5 + 1 2 · x + 2 · x 1 1 3 — 5 3 = 2 · x 3 3 · ( x 0 , 5 + 1 ) , б) a 1 4 — b 1 4 a 1 2 — b 1 2 = 1 a 1 4 + b 1 4 .

К числу основных действий с дробями относится приведение к новому знаменателю и сокращение дробей. Оба действия выполняют с соблюдением ряда правил. При сложении и вычитании дробей сначала дроби приводятся к общему знаменателю, после чего проводятся действия (сложение или вычитание) с числителями. Знаменатель остается прежним. Результатом наших действий является новая дробь, числитель которой является произведением числителей, а знаменатель есть произведение знаменателей.

Выполните действия x 1 2 + 1 x 1 2 — 1 — x 1 2 — 1 x 1 2 + 1 · 1 x 1 2 .

Решение

Начнем с вычитания дробей, которые располагаются в скобках. Приведем их к общему знаменателю:

x 1 2 — 1 · x 1 2 + 1

x 1 2 + 1 x 1 2 — 1 — x 1 2 — 1 x 1 2 + 1 · 1 x 1 2 = = x 1 2 + 1 · x 1 2 + 1 x 1 2 — 1 · x 1 2 + 1 — x 1 2 — 1 · x 1 2 — 1 x 1 2 + 1 · x 1 2 — 1 · 1 x 1 2 = = x 1 2 + 1 2 — x 1 2 — 1 2 x 1 2 — 1 · x 1 2 + 1 · 1 x 1 2 = = x 1 2 2 + 2 · x 1 2 + 1 — x 1 2 2 — 2 · x 1 2 + 1 x 1 2 — 1 · x 1 2 + 1 · 1 x 1 2 = = 4 · x 1 2 x 1 2 — 1 · x 1 2 + 1 · 1 x 1 2

Теперь умножаем дроби:

4 · x 1 2 x 1 2 — 1 · x 1 2 + 1 · 1 x 1 2 = = 4 · x 1 2 x 1 2 — 1 · x 1 2 + 1 · x 1 2

Произведем сокращение на степень x 1 2 , получим 4 x 1 2 — 1 · x 1 2 + 1 .

Дополнительно можно упростить степенное выражение в знаменателе, используя формулу разности квадратов: квадратов: 4 x 1 2 — 1 · x 1 2 + 1 = 4 x 1 2 2 — 1 2 = 4 x — 1 .

Ответ: x 1 2 + 1 x 1 2 — 1 — x 1 2 — 1 x 1 2 + 1 · 1 x 1 2 = 4 x — 1

Упростите степенное выражение x 3 4 · x 2 , 7 + 1 2 x — 5 8 · x 2 , 7 + 1 3 .
Решение

Мы можем произвести сокращение дроби на ( x 2 , 7 + 1 ) 2 . Получаем дробь x 3 4 x — 5 8 · x 2 , 7 + 1 .

Продолжим преобразования степеней икса x 3 4 x — 5 8 · 1 x 2 , 7 + 1 . Теперь можно использовать свойство деления степеней с одинаковыми основаниями: x 3 4 x — 5 8 · 1 x 2 , 7 + 1 = x 3 4 — — 5 8 · 1 x 2 , 7 + 1 = x 1 1 8 · 1 x 2 , 7 + 1 .

Переходим от последнего произведения к дроби x 1 3 8 x 2 , 7 + 1 .

Ответ: x 3 4 · x 2 , 7 + 1 2 x — 5 8 · x 2 , 7 + 1 3 = x 1 3 8 x 2 , 7 + 1 .

Множители с отрицательными показателями степени в большинстве случаев удобнее переносить из числителя в знаменатель и обратно, изменяя знак показателя. Это действие позволяет упростить дальнейшее решение. Приведем пример: степенное выражение ( x + 1 ) — 0 , 2 3 · x — 1 можно заменить на x 3 · ( x + 1 ) 0 , 2 .

Преобразование выражений с корнями и степенями

В задачах встречаются степенные выражения, которые содержат не только степени с дробными показателями, но и корни. Такие выражения желательно привести только к корням или только к степеням. Переход к степеням предпочтительнее, так как с ними проще работать. Такой переход является особенно предпочтительным, когда ОДЗ переменных для исходного выражения позволяет заменить корни степенями без необходимости обращаться к модулю или разбивать ОДЗ на несколько промежутков.

Представьте выражение x 1 9 · x · x 3 6 в виде степени.

Решение

Область допустимых значений переменной x определяется двумя неравенствами x ≥ 0 и x · x 3 ≥ 0 , которые задают множество [ 0 , + ∞ ) .

На этом множестве мы имеем право перейти от корней к степеням:

x 1 9 · x · x 3 6 = x 1 9 · x · x 1 3 1 6

Используя свойства степеней, упростим полученное степенное выражение.

x 1 9 · x · x 1 3 1 6 = x 1 9 · x 1 6 · x 1 3 1 6 = x 1 9 · x 1 6 · x 1 · 1 3 · 6 = = x 1 9 · x 1 6 · x 1 18 = x 1 9 + 1 6 + 1 18 = x 1 3

Ответ: x 1 9 · x · x 3 6 = x 1 3 .

Преобразование степеней с переменными в показателе

Данные преобразования достаточно просто произвести, если грамотно использовать свойства степени. Например, 5 2 · x + 1 − 3 · 5 x · 7 x − 14 · 7 2 · x − 1 = 0 .

Мы можем заменить произведением степени, в показателях которых находится сумма некоторой переменной и числа. В левой части это можно проделать с первым и последним слагаемыми левой части выражения:

5 2 · x · 5 1 − 3 · 5 x · 7 x − 14 · 7 2 · x · 7 − 1 = 0 , 5 · 5 2 · x − 3 · 5 x · 7 x − 2 · 7 2 · x = 0 .

Теперь поделим обе части равенства на 7 2 · x . Это выражение на ОДЗ переменной x принимает только положительные значения:

5 · 5 — 3 · 5 x · 7 x — 2 · 7 2 · x 7 2 · x = 0 7 2 · x , 5 · 5 2 · x 7 2 · x — 3 · 5 x · 7 x 7 2 · x — 2 · 7 2 · x 7 2 · x = 0 , 5 · 5 2 · x 7 2 · x — 3 · 5 x · 7 x 7 x · 7 x — 2 · 7 2 · x 7 2 · x = 0

Сократим дроби со степенями, получим: 5 · 5 2 · x 7 2 · x — 3 · 5 x 7 x — 2 = 0 .

Наконец, отношение степеней с одинаковыми показателями заменяется степенями отношений, что приводит к уравнению 5 · 5 7 2 · x — 3 · 5 7 x — 2 = 0 , которое равносильно 5 · 5 7 x 2 — 3 · 5 7 x — 2 = 0 .

Введем новую переменную t = 5 7 x , что сводит решение исходного показательного уравнения к решению квадратного уравнения 5 · t 2 − 3 · t − 2 = 0 .

Преобразование выражений со степенями и логарифмами

Выражения, содержащие с записи степени и логарифмы, также встречаются в задачах. Примером таких выражений могут служить: 1 4 1 — 5 · log 2 3 или log 3 27 9 + 5 ( 1 — log 3 5 ) · log 5 3 . Преобразование подобных выражений проводится с использованием разобранных выше подходов и свойств логарифмов, которые мы подробно разобрали в теме «Преобразование логарифмических выражений».

Этот видеоурок доступен по абонементу

У вас уже есть абонемент? Войти

Урок: Деление степеней с одинаковыми основаниями (формула )

1. Напоминание основных определений и теоремы 1

Основные определения:

Здесь a — основание степени,

n — показатель степени,

— n-ая степень числа.

Теорема 1. Для любого числа а и любых натуральных n и k справедливо равенство:

При умножении степеней с одинаковыми основаниями показатели складываются, основание остается неизменным.

Теорема 2. Для любого числа а и любых натуральных n и k, таких, что n > k справедливо равенство:

При делении степеней с одинаковыми основаниями показатели отнимаются, а основание остается неизменным.

2. Разъясняющие задачи

Вывод: частные случаи подтвердили правильность теоремы №2. Докажем ее в общем случае, то есть для любого а и любых натуральных n и k таких, что n > k.