Схема Горнера – способ деления многочлена
на бином $x-a$. Работать придётся с таблицей, первая строка которой содержит коэффициенты заданного многочлена. Первым элементом второй строки будет число $a$, взятое из бинома $x-a$:
После деления многочлена n-ой степени на бином $x-a$, получим многочлен, степень которого на единицу меньше исходного, т.е. равна $n-1$. Непосредственное применение схемы Горнера проще всего показать на примерах.
Разделить $5x^4+5x^3+x^2-11$ на $x-1$, используя схему Горнера.
Составим таблицу из двух строк: в первой строке запишем коэффициенты многочлена $5x^4+5x^3+x^2-11$, расположенные по убыванию степеней переменной $x$. Заметьте, что данный многочлен не содержит $x$ в первой степени, т.е. коэффициент перед $x$ в первой степени равен 0. Так как мы делим на $x-1$, то во второй строке запишем единицу:
Начнем заполнять пустые ячейки во второй строке. Во вторую ячейку второй строки запишем число $5$, просто перенеся его из соответствующей ячейки первой строки:
Следующую ячейку заполним по такому принципу: $1cdot 5+5=10$:
Аналогично заполним и четвертую ячейку второй строки: $1cdot 10+1=11$:
Для пятой ячейки получим: $1cdot 11+0=11$:
И, наконец, для последней, шестой ячейки, имеем: $1cdot 11+(-11)=0$:
Задача решена, осталось только записать ответ:
Как видите, числа, расположенные во второй строке (между единицей и нулём), есть коэффициенты многочлена, полученного после деления $5x^4+5x^3+x^2-11$ на $x-1$. Естественно, что так как степень исходного многочлена $5x^4+5x^3+x^2-11$ равнялась четырём, то степень полученного многочлена $5x^3+10x^2+11x+11$ на единицу меньше, т.е. равна трём. Последнее число во второй строке (ноль) означает остаток от деления многочлена $5x^4+5x^3+x^2-11$ на $x-1$. В нашем случае остаток равен нулю, т.е. многочлены делятся нацело. Этот результат ещё можно охарактеризовать так: значение многочлена $5x^4+5x^3+x^2-11$ при $x=1$ равно нулю.
Можно сформулировать вывод и в такой форме: так как значение многочлена $5x^4+5x^3+x^2-11$ при $x=1$ равно нулю, то единица является корнем многочлена $5x^4+5x^3+x^2-11$.
Разделить многочлен $x^4+3x^3+4x^2-5x-47$ на $x+3$ по схеме Горнера.
Сразу оговорим, что выражение $x+3$ нужно представить в форме $x-(-3)$. В схеме Горнера будет учавствовать именно $-3$. Так как степень исходного многочлена $x^4+3x^3+4x^2-5x-47$ равна четырём, то в результате деления получим многочлен третьей степени:
Полученный результат означает, что
$$x^4+3x^3+4x^2-5x-47=(x+3)(x^3+0cdot x^2 +4x-17)+4=(x+3)(x^3+4x-17)+4$$
В этой ситуации остаток от деления $x^4+3x^3+4x^2-5x-47$ на $x+3$ равна $4$. Или, что то самое, значение многочлена $x^4+3x^3+4x^2-5x-47$ при $x=-3$ равно $4$. Кстати, это несложно перепроверить непосредственной подстановкой $x=-3$ в заданный многочлен:
$$x^4+3x^3+4x^2-5x-47=(-3)^4+3 cdot (-3)^3-5 cdot (-3)-47=4.$$
Т.е. схему Горнера можно использовать, если необходимо найти значение многочлена при заданном значении переменной. Если наша цель – найти все корни многочлена, то схему Горнера можно применять несколько раз подряд, – до тех пор, пока мы не исчерпаем все корни, как рассмотрено в примере №3.
Найти все целочисленные корни многочлена $x^6+2x^5-21x^4-20x^3+71x^2+114x+45$, используя схему Горнера.
Коэффициенты рассматриваемого многочлена есть целые числа, а коэффициент перед старшей степенью переменной (т.е. перед $x^6$) равен единице. В этом случае целочисленные корни многочлена нужно искать среди делителей свободного члена, т.е. среди делителей числа 45. Для заданного многочлена такими корнями могут быть числа $45; ; 15; ; 9; ; 5; ; 3; ; 1$ и $-45; ; -15; ; -9; ; -5; ; -3; ; -1$. Проверим, к примеру, число $1$:
Как видите, значение многочлена $x^6+2x^5-21x^4-20x^3+71x^2+114x+45$ при $x=1$ равно $192$ (последнее число в второй строке), а не $0$, посему единица не является корнем данного многочлена. Так как проверка для единицы окончилась неудачей, проверим значение $x=-1$. Новую таблицу для этого составлять не будем, а продолжим использование табл. №1, дописав в нее новую (третью) строку. Вторую строку, в которой проверялось значение $1$, выделим красным цветом и в дальнейших рассуждениях использовать её не будем.
Можно, конечно, просто переписать таблицу заново, но при заполнении вручную это займет немало времени. Тем более, что чисел, проверка которых окончится неудачей, может быть несколько, и каждый раз записывать новую таблицу затруднительно. При вычислении «на бумаге» красные строки можно просто вычёркивать.
Итак, значение многочлена $x^6+2x^5-21x^4-20x^3+71x^2+114x+45$ при $x=-1$ равно нулю, т.е. число $-1$ есть корень этого многочлена. После деления многочлена $x^6+2x^5-21x^4-20x^3+71x^2+114x+45$ на бином $x-(-1)=x+1$ получим многочлен $x^5+x^4-22x^3+2x^2+69x+45$, коэффициенты которого взяты из третьей строки табл. №2 (см. пример №1). Результат вычислений можно также представить в такой форме:
Продолжим поиск целочисленных корней. Теперь уже нужно искать корни многочлена $x^5+x^4-22x^3+2x^2+69x+45$. Опять-таки, целочисленные корни этого многочлена ищут среди делителей его свободного члена, – числа $45$. Попробуем ещё раз проверить число $-1$. Новую таблицу составлять не будем, а продолжим использование предыдущей табл. №2, т.е. допишем в нее еще одну строку:
Итак, число $-1$ является корнем многочлена $x^5+x^4-22x^3+2x^2+69x+45$. Этот результат можно записать так:
Учитывая равенство (2), равенство (1) можно переписать в такой форме:
Теперь уже нужно искать корни многочлена $x^4-22x^2+24x+45$, – естественно, среди делителей его свободного члена (числа $45$). Проверим еще раз число $-1$:
Число $-1$ является корнем многочлена $x^4-22x^2+24x+45$. Этот результат можно записать так:
С учетом равенства (4), равенство (3) перепишем в такой форме:
Теперь ищем корни многочлена $x^3-x^2-21x+45$. Проверим еще раз число $-1$:
Проверка окончилась неудачей. Выделим шестую строку красным цветом и попробуем проверить иное число, например, число $3$:
В остатке ноль, посему число $3$ – корень рассматриваемого многочлена. Итак, $x^3-x^2-21x+45=(x-3)(x^2+2x-15)$. Теперь равенство (5) можно переписать так:
Проверим ещё раз число $3$:
Полученный результат можно записать так (это продолжение равенства (6)):
Из последней скобки видно, что число $-5$ также является корнем данного многочлена. Можно, конечно, формально продолжить схему Горнера, проверив значение $x=-5$, но необходимости в этом нет. Итак,
Числа $-1; ; 3; ; 5$ – корни данного многочлена. Причем, так как скобка $(x+1)$ в третьей степени, то $-1$ – корень третьего порядка; так как скобка $(x-3)$ во второй степени, то $3$ – корень второго порядка; так как скобка $(x+5)$ в первой степени, то $x=-5$ – корень первого порядка (простой корень).
Вообще, обычно оформление таких примеров состоит из таблицы, в которой перебираются возможные варианты корней, и ответа:
Из таблицы следует вывод, полученный нами ранее с подробным решением:
Убедиться, что числа $2$ и $-5$ являются корнями многочлена $3x^6+9x^5-28x^4+6x^3-30x^2-30x+100$. Разделить заданный многочлен на биномы $x-2$ и $x+5$.
Степень многочлена $3x^6+9x^5-28x^4+6x^3-30x^2-30x+100$ равна $6$. После деления на два заданных бинома степень заданного многочлена уменьшится на $2$, т.е. станет равна $4$.
Конечно, данный метод подбора малоэффективен в общем случае, когда корни не являются целыми числами, но для целочисленных корней метод довольно-таки неплох.
В этой статье мы расскажем об удобной схеме решения примеров на деление многочленов. Если нам нужно вычислить коэффициент частного P n ( x ) = a n a n + a n — 1 x n — 1 + . . . + a 1 x + a 0 и остаток от деления многочлена на линейный двучлен x — s , то удобно будет воспользоваться схемой (методом) Горнера.
Она заключается в создании особой таблицы и занесении в нее исходных данных:
| s i | коэффициенты многочленов | ||||
| a n | a n — 1 | a n — 2 | . . . | a 0 | |
| s | a n = b n | a n — 1 + b n · s = b n — 1 | a n — 2 + b n — 1 · s = b n — 2 | . . . | a 0 + b 1 · s = b 0 |
Числа b n , b n — 1 , b n — 2 , . . . , b 1 и будут нужными нам коэффициентами от деления P n ( x ) = a n a n + a n — 1 x n — 1 + . . . + a 1 x + a 0 на x — s . Остаток обозначен здесь как b 0 . Иначе можно записать решение так:
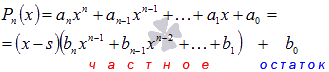
Теперь покажем , как именно применять эту схему на практике.
Условие: разделите многочлен 2 x 4 — 3 x 3 — x 2 + 4 x + 13 на линейный двучлен х — 1 , используя схему Горнера.
Решение
Заполним таблицу. У нас есть s , равный единице, и коэффициенты a 4 = 2 , a 3 = — 3 , a 2 = — 1 , a 1 = 4 , a 0 = 13 .
| s i | коэффициенты многочленов | ||||
| a 4 = 2 | a 3 = — 3 | a 2 = 1 | a 1 = 4 | a 0 = 13 | |
| s = 1 | a 4 = 2 = b 4 | a 3 + b 4 · s = = — 3 + 2 · 1 = = — 1 = b 3 | a 2 + b 3 · s = = — 1 + ( — 1 ) · 1 = = — 2 = b 2 | a 1 + b 2 · s = 4 + ( — 2 ) · 1 = = 2 = b 1 | a 0 + b 1 · s = = 13 + 2 · 1 = = 15 = b 0 |
Ответ: получили частное, равное b 4 x 3 + b 3 x 2 + b 2 x + b 1 = 2 x 3 — x 2 — 2 x + 2 , и остаток b 0 = 15 .
Во второй задаче мы обойдемся без подробных комментариев.
Условие: определите, можно ли разделить многочлен 2 x 3 — 11 x 2 + 12 x + 9 на двучлен x + 1 2 без остатка. Вычислите частное.
Решение
Заполним таблицу согласно схеме Горнера.
| s i | коэффициенты многочленов | ||||
| 2 | — 11 | 12 | 9 | ||
| — 1 2 | 2 | — 11 + 2 · — 1 2 = — 12 | 12 + — 12 · — 1 2 = 18 | 9 + 18 · — 1 2 = 0 | |
В последней ячейке мы видим нулевой остаток, следовательно, разделить исходный многочлен на двучлен можно.
Ответ: частное будет представлять из себя многочлен 2 x 2 — 12 x + 18 .
Если b 0 = 0 , то можно говорить о делимости многочлена P n ( x ) = a n a n + a n — 1 x n — 1 + . . . + a 1 x + a 0 на двучлен x — s , и мы имеем корень исходного многочлена, равный s . Используя следствие из теоремы Безу, можем представить этот многочлен в виде произведения:
P n ( x ) = a n a n + a n — 1 x n — 1 + . . . + a 1 x + a 0 = = x — s ( b n x n + 1 + b n — 1 x n — 2 + . . . + b 1 )
Благодаря этому схема Горнера хорошо подходит для тех случаев, когда нужно отыскать целые корни уравнений высших степеней, имеющих целые коэффициенты, или же разложить многочлен на простые множители.
Условие: решите уравнение x 3 — 7 x — 6 = 0 . Разложите многочлен слева на отдельные множители.
Решение
Мы знаем, что целые корни уравнения (если они есть) нужно искать среди делителей свободного члена. Запишем их отдельно 1 , — 1 , 2 , — 2 , 3 , — 3 , 6 , — 6 и проверим, используя схему Горнера.
| x i | коэффициенты многочленов | ||||
| a 3 = 1 | a 2 = 0 | a 1 = — 7 | a 0 = — 6 | ||
| 1 | 1 | 0 + 1 · 1 = 1 | — 7 + 1 · 1 = — 6 | — 6 + — 6 · 1 = — 12 | |
Из данных таблицы видно, что единица не будет входить в число корней данного уравнения.
Дополним таблицу еще одним возможным корнем.
| x i | коэффициенты многочленов | ||||
| a 3 = 1 | a 2 = 0 | a 1 = — 7 | a 0 = — 6 | ||
| 1 | 1 | 0 + 1 · 1 = 1 | — 7 + 1 · 1 = — 6 | — 6 + — 6 · 1 = — 12 | |
| — 1 | 1 | 0 + 1 · ( — 1 ) = — 1 | — 7 + — 1 · — 1 = — 6 | — 6 + ( — 6 ) · ( — 1 ) = 0 | |
А вот — 1 подходит, значит, мы можем представить исходный многочлен как x 3 — 7 x — 6 = ( x + 1 ) ( x 2 — x — 6 ) .
Проверяем делители дальше. Начнем с — 1 , поскольку возможно повторение корней, но в качестве коэффициентов будем брать значения последней строки:
| x i | коэффициенты многочленов | ||||
| a 3 = 1 | a 2 = 0 | a 1 = — 7 | a 0 = — 6 | ||
| 1 | 1 | 0 + 1 · 1 = 1 | — 7 + 1 · 1 = — 6 | — 6 + — 6 · 1 = — 12 | |
| — 1 | 1 | 0 + 1 · ( — 1 ) = — 1 | — 7 + — 1 · — 1 = — 6 | — 6 + ( — 6 ) · ( — 1 ) = 0 | |
| — 1 | 1 | — 1 + 1 · — 1 = — 2 | — 6 + — 2 · — 1 = — 4 | ||
Из этого следует, что — 1 не будет кратным (повторяющимся) корнем. Берем следующий вариант и вычисляем:
| x i | коэффициенты многочленов | ||||
| a 3 = 1 | a 2 = 0 | a 1 = — 7 | a 0 = — 6 | ||
| 1 | 1 | 0 + 1 · 1 = 1 | — 7 + 1 · 1 = — 6 | — 6 + — 6 · 1 = — 12 | |
| — 1 | 1 | 0 + 1 · ( — 1 ) = — 1 | — 7 + — 1 · — 1 = — 6 | — 6 + ( — 6 ) · ( — 1 ) = 0 | |
| — 1 | 1 | — 1 + 1 · — 1 = — 2 | — 6 + — 2 · — 1 = — 4 | ||
| 2 | 1 | — 1 + 1 · 2 = 1 | — 6 + 1 · 2 = — 4 | ||
Число 2 не входит в число корней уравнения. Дополним таблицу Горнера для х = — 2 :
| x i | коэффициенты многочленов | ||||
| a 3 = 1 | a 2 = 0 | a 1 = — 7 | a 0 = — 6 | ||
| 1 | 1 | 0 + 1 · 1 = 1 | — 7 + 1 · 1 = — 6 | — 6 + — 6 · 1 = — 12 | |
| — 1 | 1 | 0 + 1 · ( — 1 ) = — 1 | — 7 + — 1 · — 1 = — 6 | — 6 + ( — 6 ) · ( — 1 ) = 0 | |
| — 1 | 1 | — 1 + 1 · — 1 = — 2 | — 6 + — 2 · — 1 = — 4 | ||
| 2 | 1 | — 1 + 1 · 2 = 1 | — 6 + 1 · 2 = — 4 | ||
| — 2 | 1 | — 1 + 1 · — 2 = — 3 | — 6 + — 3 · — 2 = 0 | ||
Минус два будет корнем исходного уравнения. Мы можем записать многочлен так:
x 3 — 7 x — 6 = ( x + 1 ) ( x 2 — x — 6 ) = = ( x + 1 ) ( x + 2 ) ( x — 3 )
Третий и последний корень уравнения будет равен трем. Закончим заполнение таблицы, взяв значения последней полученной строки в качестве коэффициентов:
| x i | коэффициенты многочленов | ||||
| a 3 = 1 | a 2 = 0 | a 1 = — 7 | a 0 = — 6 | ||
| 1 | 1 | 0 + 1 · 1 = 1 | — 7 + 1 · 1 = — 6 | — 6 + — 6 · 1 = — 12 | |
| — 1 | 1 | 0 + 1 · ( — 1 ) = — 1 | — 7 + — 1 · — 1 = — 6 | — 6 + ( — 6 ) · ( — 1 ) = 0 | |
| — 1 | 1 | — 1 + 1 · — 1 = — 2 | — 6 + — 2 · — 1 = — 4 | ||
| 2 | 1 | — 1 + 1 · 2 = 1 | — 6 + 1 · 2 = — 4 | ||
| — 2 | 1 | — 1 + 1 · — 2 = — 3 | — 6 + — 3 · — 2 = 0 | ||
| 3 | 1 | — 3 + 1 · 3 = 0 | |||
Из этого можно сделать вывод, что последняя полученная таблица, заполненная по методу Горнера, и будет решением нашего примера. Эту задачу можно было решить и делением многочлена на линейный двучлен столбиком, однако показанная здесь схема нагляднее и проще.
Ответ: х = — 1 , х = — 2 , х = 3 , x 3 — 7 x — 6 = ( x + 1 ) ( x + 2 ) ( x — 3 ) .
Теорема Безу.
Теорема Безу, невзирая на кажущуюся простоту и очевидность, является одной из базовых теорем теории многочленов. В данной теореме алгебраические характеристики многочленов (они позволяют работать с многочленами как с целыми числами) связываются с их функциональными характеристиками (которые позволяют рассматривать многочлены как функции).
Теорема Безу утверждает, что остаток от деления многочлена 
на многочлен 
— это 
.
Коэффициенты многочлена лежат в неком коммутативном кольце с единицей (к примеру, в поле вещественных либо комплексных чисел).
Теорема Безу — доказательство.
Делим с остатком многочлен P(x) на многочлен (x-a):
Исходя из того, что deg R(x) deg (x-a) = 1 — многочлен степени не выше нуля. Подставляем 
, так как 
, получаем 
.
Но наиболее важна не именно теорема, а следствие теоремы Безу:
1. Число 
— корень многочлена P(x) тогда и только тогда, когда P(x) делится без остатка на двучлен x-a.
Исходя из этого – множество корней многочлена P(x) тождественно множеству корней соответствующего уравнения x-a.
2. Свободный член многочлена делится на любой целый корень многочлена с целыми коэффициентами (когда старший коэффициент равен единице – все рациональные корни целые).
3. Предположим, что — целый корень приведенного многочлена P(x) с целыми коэффициентами. Значит, для любого целого 
число 
делится на 
.
Теорема Безу дает возможность, найдя один корень многочлена, искать дальше корни многочлена, степень которого уже на 1 меньше: если 
, то данный многочлен P(x) будет выглядеть так:
Т.о., один корень найден и дальше находят уже корни многочлена 
, степень которого на 1 меньше степени начального многочлена. Иногда таким методом — называется понижением степени — находят все корни данного многочлена.
Теорема Безу примеры:
Найти остаток от деления многочлена 
на двучлен 
.
Теорема Безу примеры решения:
Исходя из теоремы Безу, искомый остаток соответствует значению многочлена в точке 
. Тогда найдем 
, для этого значение подставляем в выражение для многочлена 
вместо 
. Получаем:
Ответ: Остаток = 5.
Схема Горнера.
Схема Горнера – это алгоритм деления (деление схемой Горнера) многочленов, записываемый для частного случая, если частное равно двучлену 
.
Построим этот алгоритм:
Предположим, что 
— делимое
— частное (его степень, вероятно, будет на удиницу меньше), r — остаток (т.к. деление осуществляется на многочлен 1-ой степени, то степень остатка будет на единицу меньше, т.е. нулевая, таким образом, остаток это константа).
По определению деления с остатком P(x) = Q(x) (x–a) + r. После подстановки выражений многочленов получаем:
Раскрываем скобки и приравниваем коэффициенты при одинаковых степенях, после чего выражаем коэффициенты частного через коэффициенты делимого и делителя:
Удобно вычисления сводить в такую таблицу:
В ней выделены те клетки, содержимое которых участвует в вычислениях на очередном шаге.
Схема Горнера примеры:
Пусть надо поделить многочлен 
на двучлен x–2.
Составляем таблицу с двумя строками. В 1 строку выписываем коэффициенты нашего многочлена. Во второй строке будем получать коэффициенты неполного частного по следующей схеме: в первую очередь переписываем старший коэффициент данного многочлена, далее, дабы получить очередной коэффициент, умножаем последний найденный на а=2 и складываем с соответствующим коэффициентом многочлена F(x). Самый последний коэффициент будет остатком, а все предыдущие – коэффициентами неполного частного.