Матрица жесткости конечного элемента

Рассмотрим произвольный конечный элемент с числом степеней свободы n_ст.

Вектором узловых перемещений конечного элемента называется вектор, складывающийся из значений перемещений его узлов по направлению всех его степеней свободы. Очевидно, размерность вектора узловых перемещений равна числу степеней свободы элемента n_ст.

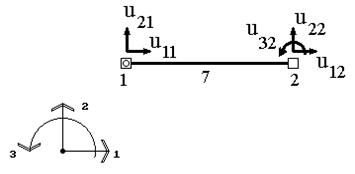
Рис.17.9

Например, для двухузлового элемента, имеющего в конечно-элементной схеме номер 7, характеризующегося тремя степенями свободы (рис.17.9), вектор узловых перемещений будет иметь следующий вид: .

Здесь введены следующие обозначения: 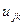— перемещение узла k по направлению j, -вектор узловых перемещений узла е. Понятно, что если узел k шарнирный, то j может быть равно 1 или 2. Если же узел k жесткий, то j может быть равно 1, 2 или 3.

Аналогично вводится вектор узловых усилий, действующих на элемент. Его компонентами являются усилия, приложенные к элементу в узлах и действующие по направлению всех его степеней свободы. Для приведенного на рис.17.9 элемента этот вектор будет иметь вид (рис.17.10): .

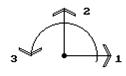
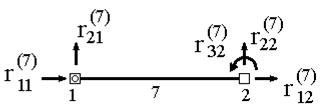
Рис.17.10

Здесь вводятся обозначения: 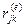— усилие, действующее на узел k элемента е по направлению j, 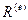— вектор узловых сил, действующих на элемент е.

Вектора R (e) и U (e) являются блочными, т.е. в них можно выделить блоки и 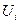соответственно, содержащие усилия и перемещения, относящиеся к i-ому узлу элемента.

Если узел i — жесткий, то 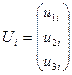, если шарнирный, то 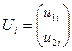. Аналогично выглядят и блоки вектора R (e) .

Например, для рассматриваемого элемента (рис.17.9 и рис.17.10):

, .

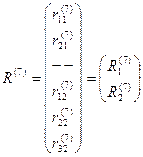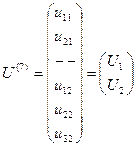Понятно, что при деформировании элемента в результате смещения одного из его узлов по направлению одной из степеней свободы на узлы элемента должны действовать внешние силы, препятствующие возвращению элемента в недеформируемое состояние. Подобная ситуация может возникнуть, например, при неравномерных осадках в опорах статически неопределимой стержневой системы (рис.17.11), реакции, возникшие в опорах, препятствуют возвращению конструкции в недеформированное состояние.

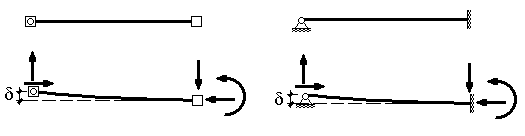
Рис.9.11

В рамках гипотезы линейного деформирования связь между перемещениями узлов элемента и силами, действующими при этом на него, должна быть линейной. Например, с увеличением смещения d вдвое, все усилия, действующие на узлы элемента также должны увеличиться вдвое.

Основной характеристикой конечного элемента является матрица жесткости элемента 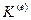. Она связывает вектор узловых перемещений и вектор приложенных к элементу узловых усилий 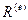соотношением:

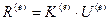, (17.2)

выражающим линейный характер связи между действующими на узлы силами и узловыми перемещениями. Матрица жесткости элемента играет роль, аналогичную коэффициенту жесткости пружины К, связывающего приложенное к ней усилие R, и вызванное этим усилием перемещение U соотношением (рис.9.12) .

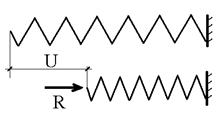
Рис.17.12

Поскольку вектора и 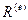имеют размерность 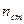, число строк и столбцов в матрице 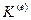тоже должно быть равным :

.

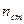Введем обозначение — усилие, действующее на узел m элемента e по направлению i, от единичного перемещения узла k этого же элемента е по направлению j при условии, что перемещения по направлению всех остальных степеней свободы в элементе равны нулю. Например, 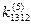— усилие, действующее на узел 1 элемента 5 по направлению 1 при единичном перемещении узла 2 этого же элемента 5 по направлению 3, а 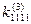— усилие, действующее на узел 1 элемента 3 по направлению 1 от единичного смещения этого же узла по этому же направлению. Последнее значение, как и любое значение 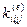в соответствии с теоремой Клапейрона всегда положительно, аналогично коэффициентам 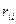в уравнениях классического метода перемещений.

Важно четко помнить порядок индексов, стоящих при k. Верхний индекс — это номер элемента. Первые два нижних индекса — направления, причем первый из них — номер направления определяемого усилия, а второй — номер направления, в котором произошло единичное перемещение. Вторые два нижних индекса — номера узлов элемента, причем первый из них — номер узла, в котором определяется усилие, второй — в котором задано единичное перемещение.

Для рассматриваемого элемента (рис.17.9 и рис.17.10) матрица жесткости элемента имеет следующий вид:

.

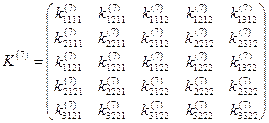Легко увидеть, что каждый столбец этой матрицы состоит из усилий, действующих на узлы элемента при единичном смещении по направлению какой-либо из его степеней свободы при условии, что перемещения по направлению остальных степеней свободы равны нулю.

Например, первый столбец представляет собой усилия, действующие на узлы элемента при единичном смещении узла 1 (4-ый индекс при коэффициентах) по направлению 1 (2-ой индекс при коэффициентах) при условии, что перемещения по направлению остальных степеней свободы равны нулю. Второй столбец представляет собой усилия, действующие на узлы элемента при единичном смещении узла 1 (4-ый индекс при коэффициентах) по направлению 2 (2-ой индекс при коэффициентах) при условии, что перемещения по направлению остальных степеней свободы равны нулю (рис.17.13). И так далее.

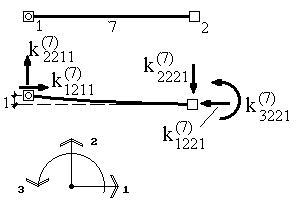
Рис.17.13

Докажем, что это действительно так, например, для первого столбца матрицы жесткости.

Зададим перемещение узла 1 по направлению 1 элемента равным 1, в то время как все его остальные узловые перемещения будем считать равными нулю. В этом случае вектор узловых перемещений приобретает вид 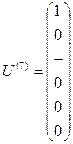, и равенство (9.2) становится следующим: .

,

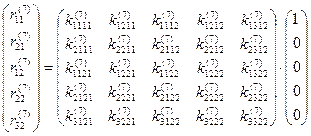т.е. компоненты первого столбца матрицы жесткости на самом деле оказались равными компонентам вектора усилий, действующих на узлы элемента при заданном смещении.

Придавая соответствующий вид вектору узловых перемещений, можно выполнить аналогичное доказательство для любого другого столбца матрицы жесткости элемента.

Для рассматриваемого элемента (рис.17.9) запишем матричное равенство (17.2) в развернутом виде:

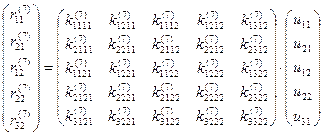
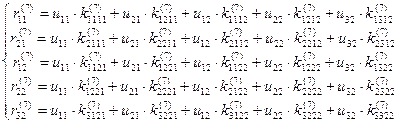
Физический смысл любого из уравнений данной системы очевиден.

Если узел k элемента е получает по направлению j единичное перемещение, то усилие, действующее при этом на узел m по направлению i равно. Если же это перемещение будет равно не единице, а 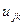, то в соответствии с линейным законом связи между усилиями и перемещениями, рассматриваемое усилие увеличится также в 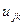раз и составит .

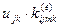Пусть теперь все узлы элемента получают смещения по направлению всех имеющихся у элемента степеней свобод. Тогда, в соответствии с принципом суперпозиций, усилие 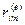, т.е. усилие, действующее на какой- либо узел m по какому-либо направлению i, будет представлять собой сумму усилий, вызванных смещениями всех узлов элемента по направлению всех имеющихся степеней свобод (рис.17.14). Поскольку, как мы только что выяснили, при перемещении какого-либо узла k по направлению j на величину 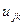на узел m по направлению i будет действовать усилие 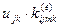, суммарное усилие, действующее на узел m по направлению j, будет представлять собой сумму величин 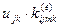для всех степеней свободы элемента (рис.9.14).

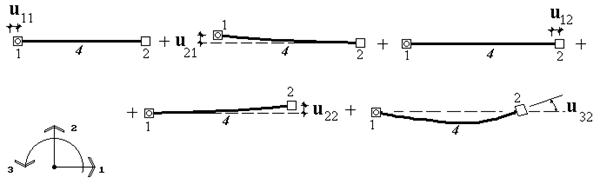
Рис.17.14

Формально это можно записать следующим образом:

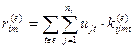, (9.3)

где t— номер узла, входящего в элемент е, запись 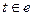означает, что суммирование производится по всем узлам, входящим в элемент е, n_t — число степеней свободы в узле t. Причем, n_t=2, если узел t — шарнирный, и n_t=3, если узел t жесткий.

Как мы уже выяснили, элементы, стоящие на главной диагонали матрицы жесткости элемента должны быть положительными. Кроме того, матрица жесткости элемента должна быть симметричной. Действительно, в соответствии с теоремой взаимности реакций, усилие, действующее на узел m по направлению i, от единичного перемещения узла k этого же элемента по направлению j должно равняться усилию, действующему на узел k по направлению j, от единичного перемещения узла m этого же элемента по направлению i, т.е. .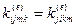

Аналогично векторам 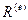и матрица жесткости элемента 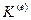также является блочной. Она состоит из блоков , каждый из которых содержит коэффициенты, связывающие перемещения k-го узла элемента и реакции, возникающие при этом, в m-ом узле данного элемента.

Например, для рассматриваемого элемента (рис.17.9):

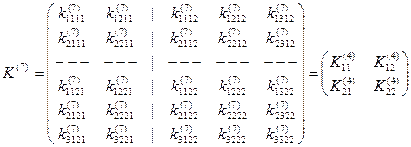
|	следующая лекция ==>
Основные определения метода конечных элементов	|	Преобразование матрицы жесткости при переходе от одной системы координат к другой

Дата добавления: 2014-01-04 ; Просмотров: 1084 ; Нарушение авторских прав? ;

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Как отмечалось выше, часто в двумерных краевых задачах для ДУЧП используют треугольный и четырехугольный КЭ.

Построим линейную функцию формы для треугольного элемента. Используем аппроксимацию

Координаты вершин треугольного элемента, положим, равны (*/, У,)> ( х р y)i ( х к’ У к)- Значения аппроксимирующей функции v(x, у) в указанных узлах обозначим v_/5 v_y., v_k соответственно.

В указанных обозначениях и соглашениях имеем следующую СЛАУ относительно неизвестных коэффициентов аппроксимирующей функции а, Ь, с:

Решение этой СЛАУ имеет вид

где А — площадь конечного элемента.

Таким образом, искомую линейную функцию формы определяет выражение (3.32) с найденными коэфициентами а, Ь, с (рис. 3.25).

Рис. 3.25. Линейная функция формы треугольного элемента

Функции формы прямоугольного четырехугольного элемента с узлами i,j, к, I можно получить, например, в виде произведения одномерных линейных базисных функций:

Здесь L_x, L_y — длины сторон КЭ. Конечный элемент с такими глобальными базисными функциями называют билинейным.

На этом этапе используется метод взвешенных невязок в пределах одного конечного элемента (см. пример ниже).

Ансамблирование проводится с целью получения полной МКЭ- модели объекта на основе локальных матриц жесткости и векторов нагрузок всех КЭ модели. Основными результатами ансамблирования являются глобальная матрица жесткости и глобальный вектор нагрузок.

Положим, что рассматривается некоторая двумерная краевая задача для ДУЧП и используются треугольные КЭ. Тогда локальная матрица жесткости треугольного элемента с узлами ij, к имеет вид

Таким образом, например, КЭ с узлами i = 7,j = 5,k = 4 (рис. 3.26), дает аддитивный вклад в элементы глобальной матрицы жесткости кц к₇₅ к₁₄ к₅₁ к₅₅ к₅₄ к₄₁ к₄₅ к_и.

Рис. 3.2В. Пример двумерного объекта покрытого треугольными КЗ

Структура глобальной матрицы жесткости для объекта, представленного на рис. 3.26, приведена в табл. 3.4, где символом «*» обозначены ненулевые элементы.

Структура глобальной матрицы жесткости для объекта, представленного на рис. 3.26

Для расчета конструкций, испытывающих плоское напряженное состояние, плоский треугольный конечный элемент явяляется одним из наиболее удобных типов конечных элементов, т.к. позволяет наиболее просто и удобно получить на конструкции сетку узлов требуемой густоты.

Рассмотрим процесс формирования матрицы жесткости плоского треугольного 3-х узлового конечного элемента с узлами i, j, m, обозначенными в направлении обхода против часовой стрелки.

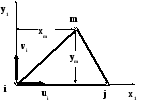
К построению матрицы жесткости треугольного КЭ

Смещения в узле имют 2 компонента — u_iиv_i. Тогда вектор узловых смещений элемента может быть представлен как

(1)

Самое простое представление смещения uиvточек с координатамиxиyвнутри элемента через смещения узловых точек может быть получено на основе использования 2-х линейных многочленов:

(2)

Постоянные __можно получить, решая две системы из 3-х уравнений, введя координаты узлов и приравняв их смещения соответствующим узловым смещениям:

(3)

Подставив решения систем (3) в выражения (2) окончательно получим выражения для uиv

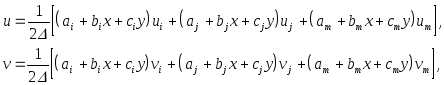(4)

где - площадь треугольника,

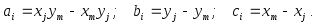
Относительная деформация в любой точке элемента определяется с помощью трех компонентов, вносящих вклад во внутреннюю работу, которая с помощью уравнений (4) может быть записана как

(5)

Учитывая, что для треугольного элемента постоянной толщины общее выражение для матрицы жесткости может быть упрощено, т.е.

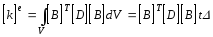(6)

и учитывая, что матрица упругости ( закона Гука) для случая плоского напряженного состояния имеет вид

(7)

окончательно выражение для матрицы жесткости плоского треугольного элемента имеет вид:

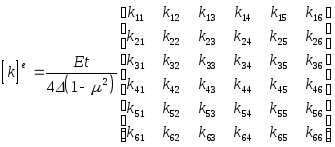(8)

где

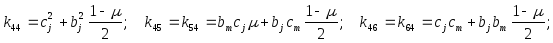
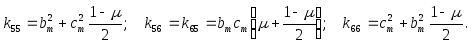
Использование полученной матрицы жесткости в дальнейших конечно-элементных операциях ничем не отличается от использования матрицы жесткости стержневого конечного элемента. Естественно, результатом расчета в этом случае будут усилия соответствующие компонентам перемещений, указанным на Рис. , т.е. 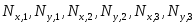, которые могут быть преобразованы к напряжениям в центре тяжести конечного элемента.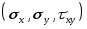