Функция треугольного закона распределения симпсона имеет вид

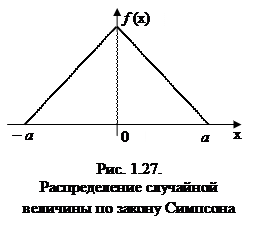
К распределению по закону Симпсона приводит сложение двух случайных величин, подчиненных закону равной вероятности при одинаковых параметрах рассеяния. Кривая рассеяния имеет вид равнобедренного треугольника (рис. 1.27), из-за чего закон Симпсона часто называют законом треугольника.

При выборе в качестве начала отсчета случайной величины ее плотность распределения и математическое ожидание имеют следующий вид:

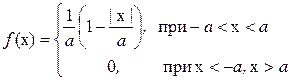, (1.63)

M_x = 0 , 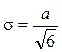, 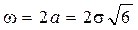. (1.64)

Не нашли то, что искали? Воспользуйтесь поиском:

Лучшие изречения: На стипендию можно купить что-нибудь, но не больше. 9137 — | 7300 — или читать все.

91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.

Отключите adBlock!
и обновите страницу (F5)
очень нужно

Функция треугольного распределения случайной величины определяется формулой:

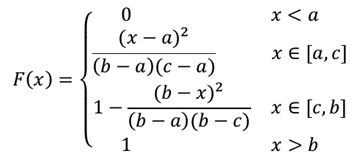
Плотность треугольного распределения СВ находится по формуле:

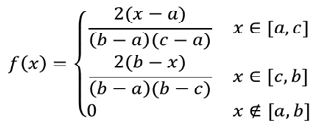
Математическое ожидание — формула:

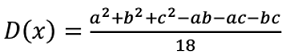
График плотности треугольного распределения случайной величины в диапазоне от -4 до 10

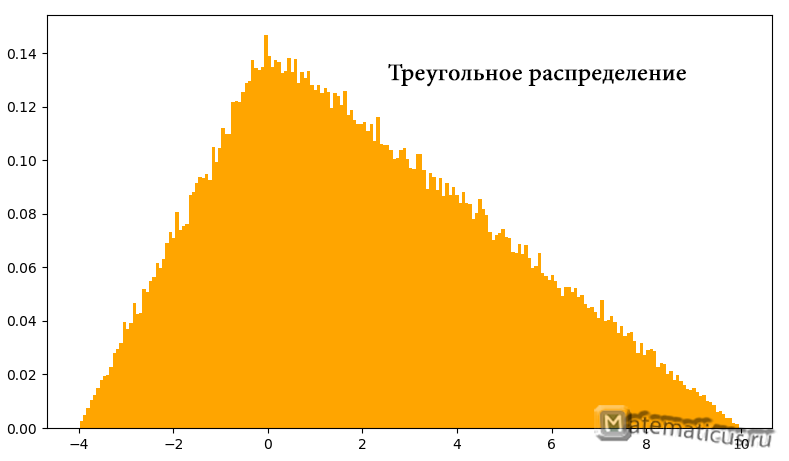
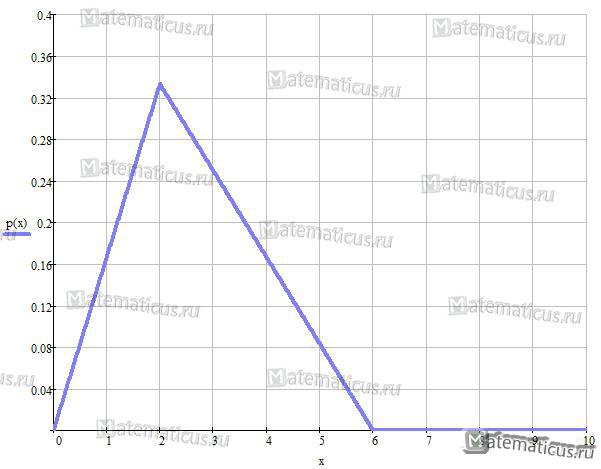
График плотности треугольного распределения случайной величины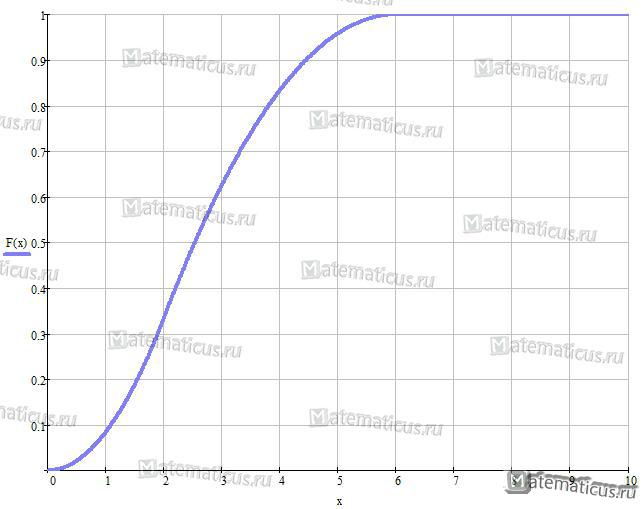

График функции треугольного распределения случайной величины

Треугольное распределения является приблизительной моделью и применяется, когда недостаточно данных или они отсутствуют. Треугольный закон распределения также используется для построения сложных законов распределения.

Он характерен для случайных погрешностей цифровых приборов, в которых измеряемая величина преобразуется в пропорциональный интервал времени Т_сч, называемый временем счета, а измерение этого интервала выполняется с помощью счетных импульсов стабильного генератора, имеющих период следования Т. В связи со случайным положением счетных импульсов относительно интервала Т_сч, а также случайным соотношением между периодом Т и временем счета Т_сч треугольный закон представляет собой композицию (объединение) двух равномерных законов с одинаковыми по величине максимальными погрешностями.

Функция распределения одномерной плотности вероятности случайных погрешностей для треугольного закона задается следующими соотношениями:

(46) где

График треугольного закона распределения приведен на рисунке 20.

Математическое ожидание величины x: определяется по той же формуле, что и равномерное:

Рисунок 20 — Треугольное распределение случайной величины

Среднее квадратическое отклонение определяется по формуле: