В этом материале мы объясним, что такое положительные и отрицательные числа. После того, как будут сформулированы определения, мы покажем на примерах, что это такое, и раскроем основной смысл этих понятий.
Что такое положительные и отрицательные числа
Для того чтобы объяснить основные определения, нам понадобится координатная прямая. Она будет расположена горизонтально и направлено слева направо: так будет удобнее для понимания.
Положительные числа – это те числа, которые соответствуют точкам в той части координатной прямой, которая расположена справа от начала отсчета.
Отрицательные числа – это те числа, которые соотносятся с точками в части координатной прямой, расположенной с левой стороны от начала отсчета (нуля).
Нуль, от которого выбираем направления, сам по себе не относится ни к отрицательным, ни к положительным числам.
Из данных выше определений следует, что положительные и отрицательные числа образуют некие множества, противоположные друг другу (положительные противопоставляются отрицательным, и наоборот). Ранее мы об этом уже упоминали в рамках статьи о противоположных числах.
Мы всегда записываем отрицательные числа с минусом.
После того, как мы ввели основные определения, мы можем без труда привести примеры. Так, к положительным относятся любые натуральные числа – 1 , 9 , 134 345 и др. Положительные рациональные числа – это, например, 7 9 , 76 2 3 , 4 , 65 и 0 , ( 13 ) = 0 , 126712 . и так далее. К положительным иррациональным числам относится число π , число e , 9 5 , 809 , 030030003 … (это так называемая бесконечная непериодическая десятичная дробь).
Приведем примеры отрицательных чисел. Это — 2 3 , − 16 , − 57 , 58 − 3 , ( 4 ) . Иррациональные отрицательные числа – это, например, минус пи, минус e и др.
Можно ли сразу сказать, что значение числового выражения log 3 4 — 5 является отрицательным числом? Ответ неочевиден. Нам придется выразить это значение десятичной дробью и потом посмотреть (подробнее см. в материале о сравнении действительных чисел).
Для того чтобы уточнить, что число положительное, перед ним иногда ставят плюс, так же, как и перед отрицательным – минус, но чаще всего он опускается. Не забывайте, что + 5 = 5 , + 1 2 3 = 1 2 3 , + 17 = 17 и так далее. По сути, это разные обозначения одного и того же числа.
В литературе также можно встретить определения положительных и отрицательных чисел, данные на основе наличия у них того или иного знака.
Положительное число – это число, имеющее знак плюс, а отрицательное – имеющее знак минус.
Есть также определения, основанные на положении данного числа относительно нуля (вспомним, что на правой стороне координатной прямой расположены большие числа, а на левой — меньшие).
Положительные числа – это все числа, значение которых больше нуля. Отрицательные числа – это все числа, меньшие нуля.
Выходит, что нуль является своеобразным разделителем: он отделяет отрицательные числа от положительных.
Отдельно остановимся на том, как правильно читать записи положительных и отрицательных чисел, хотя, как правило, с этим не возникает особых проблем. Для отрицательных чисел мы всегда озвучиваем минус, т.е. — 1 2 5 – это «минус одна целая две пятых».
В случае положительных чисел мы озвучиваем плюс только тогда, когда он явно указан в записи, т.е. + 7 – это «плюс семь». Названия математических знаков неправильно склонять по падежам. Например, верно будет прочесть фразу a = — 5 как « а равно минус пяти», а не «минусу пяти».
Основной смысл положительных и отрицательных чисел
Мы уже дали основные определения, но для того, чтобы делать верные подсчеты, необходимо понять сам смысл положительности или отрицательности числа. Попробуем помочь вам это сделать.
Положительные числа, то есть те, которые больше 0 , мы рассматриваем как прибыль, прибавку, увеличение количества чего-либо, а отрицательные – недостаток, убыток, расход, долг. Приведем примеры:
У нас есть 5 любых предметов, например, яблок. Цифра 5 – положительная, она указывает на то, что у нас что-то есть, мы обладаем некоторым количеством реально существующих предметов. А как тогда рассматривать — 5 ? Оно может, например, значить, что мы должны отдать кому-то пять яблок, которых у нас в данное время нет.
Проще всего это понять на примере денег: если у нас есть 6 , 75 тыс. рублей, то наш доход положительный: нам дали денег, и они у нас есть. В то же время в кассе эти расходы указываются как — 6 , 75 , то есть для них это убыток.
На градуснике рост температуры на 4 , 5 значений можно описать как + 4 , 5 , а снижение, в свою очередь, как — 4 , 5 . В приборах, предназначенных для измерения, часто используются положительные и отрицательные числа, поскольку с помощью них удобно отображать изменения величин. Например, в термометре отрицательные числа указываются синим цветом – это падение, холод, уменьшение тепла; положительные же отмечены красным – это цвет огня, роста, увеличения тепла. Эти цвета очень часто используются для записи таких чисел, т.к. они очень наглядны – с их помощью всегда можно четко выделить приход и расход, прибыток и убыток.
Положительные числа — это числа со знаком «+» перед ними. Знак «+» обычно не пишется (если перед числом не написан знак, то, по умолчанию, это число со знаком «+»).
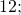
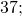
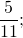
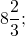
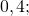
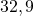
— положительные числа. Перед этими числами не записан знак, значит, по умолчанию, перед ними стоит знак «плюс» (это сокращенная форма записи
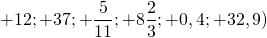
Таким образом, +12=12, то есть +12 и 12 — это одно и то же число, только по-разному обозначенное.
Любое положительное число больше нуля.
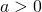0]" title="Rendered by QuickLaTeX.com"/>
означает, что число a — положительное.
Все натуральные числа являются положительными.
На координатной прямой все положительные числа расположены правее нуля.
Любое положительное число на координатной прямой лежит правее любого отрицательного числа.
положительные числа 1; 2; 3; 5,2; 7 2/3 лежат правее нуля и правее отрицательных чисел -2; -1.
Число нуль не является ни положительным, ни отрицательным. Оно отделяет положительные числа от отрицательных.
Отрицательные числа подчиняются практически тем же правилам, что и натуральные, но имеют некоторые особенности.
- Если любое множество положительных чисел ограничено снизу, то любое множество отрицательных чисел ограничено сверху.
- При умножении целых чисел действует правило знаков: произведение чисел с разными знаками отрицательно, с одинаковыми — положительно.
- При умножении обеих частей неравенства на отрицательное число знак неравенства меняется на обратный. Например, умножая неравенство 3 −10.
- При делении с остатком частное может иметь любой знак, но остаток, по соглашению, всегда неотрицателен (иначе он определяется не однозначно). Например, разделим −24 на 5 с остатком:
.
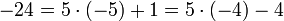Исторический очерк
Древний Египет, Вавилон и Древняя Греция не использовали отрицательных чисел, а если получались отрицательные корни уравнений (при вычитании), они отвергались как невозможные.
Впервые отрицательные числа были частично узаконены в Китае, а затем (примерно с VII века) и в Индии, где трактовались как долги (недостача), или признавались как промежуточный этап, полезный для вычисления окончательного, положительного результата. Правда, умножение и деление для отрицательных чисел тогда ещё не были определены.
Диофант в III веке уже знал правило знаков и умел умножать отрицательные числа. Однако и он рассматривал их лишь как временные значения.
Полезность и законность отрицательных чисел утверждались постепенно. Индийский математики Брахмагупта (VII век) уже рассматривал их наравне с положительными. В Европе признание наступило на тысячу лет позже, да и то долгое время отрицательные числа называли «ложными», «мнимыми» или «абсурдными». Даже Паскаль считал, что 0 − 4 = 0 , так как ничто не может быть меньше, чем ничто. Бомбелли и Жирар, напротив, считали отрицательные числа вполне допустимыми и полезными, в частности, для обозначения недостачи чего-либо. Отголоском тех времён является то обстоятельство, что в современной арифметике операция вычитания и знак отрицательных чисел обозначаются одним и тем же символом (минус), хотя алгебраически это совершенно разные понятия.
В XVII веке, с появлением аналитической геометрии, отрицательные числа получили наглядное геометрическое представление на числовой оси. С этого момента наступает их полное равноправие. Тем не менее теория отрицательных чисел долго находилась в стадии становления. Оживлённо обсуждалась, например, странная пропорция 1:(-1) = (-1):1 — в ней первый член слева больше второго, а справа — наоборот, и получается, что большее равно меньшему («парадокс Арно»). Непонятно было также, какой смысл имеет умножение отрицательных чисел, и почему произведение отрицательных положительно; на эту тему проходили жаркие дискуссии.
Полная и вполне строгая теория отрицательных чисел была создана только в XIX веке (Уильям Гамильтон и Герман Грассман).