Определение . Непрерывной называют случайную величину, которая может принимать все значения из некоторого конечного или бесконечного промежутка.
Для непрерывной случайной величины вводится понятие функции распределения.
Определение. Функцией распределения вероятностей случайной величины Х называют функцию F(х), определяющую для каждого значения x вероятность того, что случайная величина Х примет значение меньшее x, то есть:
F(х) = P(X x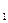 
,
то F(x 
) ≥ F(x ).
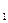3. Вероятность того, что случайная величина примет значение, заключенное в интервале [a; b), равна приращению функции распределения на этом интервале:
P(a ≤ X Определение . Плотностью распределения вероятностей непрерывной случайной величины называют первую производную от функции распределения:
Часто вместо термина «плотность распределения вероятностей» используют термин «плотность вероятностей» и «дифференциальная функция».
Свойства плотности распределения:
1. Плотность распределения неотрицательна в любой точке оси Ох:
f(x)≥0 при х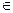 
(– ∞; +∞).
2. Вероятность того, что непрерывная случайная величина Х примет значение, принадлежащее интервалу (а, b), определяется равенством:
P(a Определение. Математическое ожидание непрерывной случайной величины Х, возможные значения которой принадлежат всей оси Ох, определяется равенством
М(Х)= 
,
где f(x) – плотность распределения случайной величины Х.
Предполагается, что интеграл сходится абсолютно. В частности, если все возможные значения принадлежат интервалу (a;b), то
М(Х)= 
.
Математическое ожидание обладает следующими свойствами:
1. Математическое ожидание постоянной величины равно самой постоянной:
2. Математическое ожидание суммы случайных величин равно сумме математических ожиданий слагаемых:
.
3. Постоянный множитель можно выносить за знак математического ожидания:
.
4. Математическое ожидание произведения взаимно независимых случайных величин равно произведению математических ожиданий сомножителей:
.
Определение . Дисперсия непрерывной случайной величины Х, возможные значения которой принадлежат всей оси Ох, определяется равенством:
D(x)= 
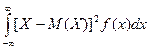
Как и в случае с дискретной случайной величиной, можно показать, что
D(x)= 
В частности, если все возможные значения Х принадлежат интервалу (a;b), то
D(X)= 
D(X)= 
.
Дисперсия обладает следующими свойствами:
1. Дисперсия постоянной равна нулю:
2. Постоянный множитель можно выносить за знак дисперсии, предварительно возведя его в квадрат:
D(CХ)=C 
D(Х).
3. Дисперсия суммы независимых случайных величин равна сумме дисперсий слагаемых:
.
4. Дисперсия произведения независимых случайных величин равна произведению дисперсий сомножителей:
.
5. Дисперсия суммы постоянной и независимой случайной величины равна квадрату постоянной на дисперсию независимой случайной величины:
.
Пример. Дана функция распределения непрерывной случайной величины Х
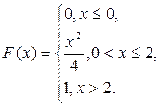
4. Математическое ожидание М(Х),
6. Среднее квадратическое отклонение σ,
1. Построим график функции распределения
 |
Рис. 2. График функции распределения.
2. Так как плотность f(x) равна первой производной от функции распределения
то найдем производные от каждой из функций, составляющих функцию F(x):
.
Тогда получаем функцию f(x):
f(x)=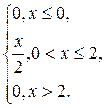 
3. Построим график плотности f(x)
Рис. 3. График плотности f(x).
Заметим, что при х = 0 производная F′(х) не существует.
4. Найдем математическое ожидание непрерывной случайной величины Х:
М(Х)=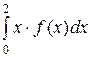 
= 
= 
= 
= 
= 
.
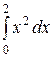5. Чтобы найти дисперсию непрерывной случайной величины Х, найдём математическое ожидание случайной величины Х :
М(Х )= 
= 
= 
= 
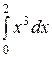=2.
Дисперсию найдем по формуле:
D(Х) = M(Х ) – M (Х) = 2- 
= 2 -1,78 = 0,22.
6. Среднее квадратическое отклонение σ найдем по формуле:
σ(X) = 
= 
= 0,47.
7. Найдем вероятность того, что случайная величина Х примет значение из интервала (– 
;– 2), то есть Р(Х
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Как то на паре, один преподаватель сказал, когда лекция заканчивалась — это был конец пары: "Что-то тут концом пахнет". 8526 — 
| 8113 — 
или читать все.
91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
Непрерывную с. в. можно задать, используя функцию, которую называют плотностью распределения или плотностью вероятности, или дифференциальной функцией распределения.
Плотностью распределения вероятностей непрерывной с. в. Х называют функцию f(x) – первую производную от функции распределения F(x):
Из этого определения следует, что функция распределения является первообразной для плотности распределения.
Для описания распределения вероятностей дискретной с. в. плотность распределения не применима.
Вероятностный смысл плотности распределения.
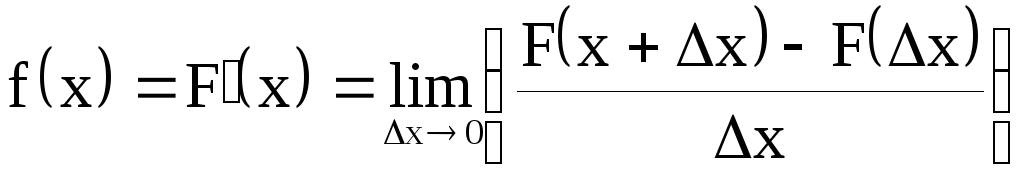
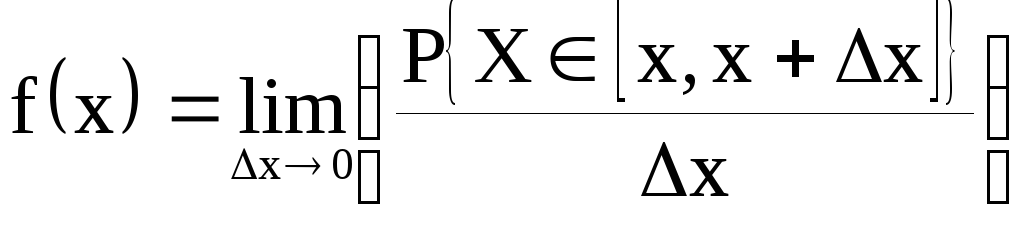
Таким образом, предел отношения вероятности того, что непрерывная с. в. примет значение, принадлежащее интервалу (x, x +∆x), к длине этого интервала (при ∆x → 0) равен значению плотности распределения в точке х.
Функция плотности характеризует каждое значение непрерывной случайной величины в отдельности, а не целый диапазон как это имеет место для функции распределения.
Вероятность попадания непрерывной с. в. в заданный интервал.
В книжной версии
Том 26. Москва, 2014, стр. 448
Скопировать библиографическую ссылку:
ПЛО́ТНОСТЬ ВЕРОЯ́ТНОСТИ, плотность распределения вероятностей случайной величины $X$ , функция $p(x), -∞lt x lt ∞$ , такая, что $$p(x)⩾0, intlimits_<-infty>^ <infty>p(x)dx=1$$ и при любых $alt b$ вероятность события $alt Xlt b$ равна $$intlimits_a^b p(x)dx.$$ Если $p(x)$ непрерывна, то при достаточно малых $Δx$ вероятность неравенства $xlt Xlt x+Δx$ приближённо равна $p(x)Δx$ (с точностью до малых более высокого порядка). Функция распределения $F(x)$ случайной величины $X$ , имеющей плотность, связана с П. в. равенствами $$F(x)=intlimits_<-infty>^x p(u)du, -∞lt xlt ∞,$$ и, если $F(x)$ дифференцируема, $p(x)=F′(x)$ .