Удельная тепловая мощность тока формула

Работа и мощность тока. Закон Джоуля – Ленца

Рассмотрим произвольный участок цепи, к концам которого приложено напряжение U. За время dt через каждое сечение проводника проходит заряд При этом силы электрического поля, действующего на данном участке, совершают работу: Разделив работу на время, получим выражение для мощности:

(7.7.1)

Полезно вспомнить и другие формулы для мощности и работы:

(7.7.2)

(7.7.3)

В 1841 г. манчестерский пивовар Джеймс Джоуль и в 1843 г. петербургский академик Эмилий Ленц установили закон теплового действия электрического тока.

Джоуль Джеймс Пресскотт (1818 – 1889) – английский физик, один из первооткрывателей закона сохранения энергии. Первые уроки по физике ему давал Дж. Дальтон, под влиянием которого Джоуль начал свои эксперименты. Работы посвящены электромагнетизму, кинетической теории газов.

Ленц Эмилий Христианович (1804 – 1865) – русский физик. Основные работы в области электромагнетизма. В 1833 г. установил правило определения электродвижущей силы индукции (закон Ленца), а в 1842 г. (независимо от Дж. Джоуля) – закон теплового действия электрического тока (закон Джоуля-Ленца). Открыл обратимость электрических машин. Изучал зависимость сопротивление металлов от температуры. Работы относятся также к геофизике.

Независимо друг от друга Джоуль и Ленц показали, что при протекании тока, в проводнике выделяется количество теплоты:

(7.7.4)

Если ток изменяется со временем, то

.

Это закон Джоуля–Ленца в интегральной форме.

Отсюда видно, что нагревание происходит за счет работы, совершаемой силами поля над зарядом.

Соотношение (7.7.4) имеет интегральный характер и относится ко всему проводнику с сопротивлением R, по которому течет ток I. Получим закон Джоуля-Ленца в локальной-дифференциальной форме, характеризуя тепловыделение в произвольной точке.

Тепловая мощность тока в элементе проводника Δl, сечением ΔS, объемом равна:

.

Удельная мощность тока

.

Согласно закону Ома в дифференциальной форме . Отсюда закон Джоуля — Ленца в дифференциальной форме характеризующий плотность выделенной энергии:

,

(7.7.5)

Так как выделенная теплота равна работе сил электрического поля

,

то мы можем записать для мощности тока:

.

(7.7.6)

Мощность, выделенная в единице объема проводника .

Приведенные формулы справедливы для однородного участка цепи и для неоднородного.

Работа и мощность тока. Закон Джоуля – Ленца

Рассмотрим произвольный участок цепи, к концам которого приложено напряжение U. За время dt через каждое сечение проводника проходит заряд При этом силы электрического поля, действующего на данном участке, совершают работу: Разделив работу на время, получим выражение для мощности:

(7.7.1)

Полезно вспомнить и другие формулы для мощности и работы:

(7.7.2)

(7.7.3)

В 1841 г. манчестерский пивовар Джеймс Джоуль и в 1843 г. петербургский академик Эмилий Ленц установили закон теплового действия электрического тока.

Джоуль Джеймс Пресскотт (1818 – 1889) – английский физик, один из первооткрывателей закона сохранения энергии. Первые уроки по физике ему давал Дж. Дальтон, под влиянием которого Джоуль начал свои эксперименты. Работы посвящены электромагнетизму, кинетической теории газов.

Ленц Эмилий Христианович (1804 – 1865) – русский физик. Основные работы в области электромагнетизма. В 1833 г. установил правило определения электродвижущей силы индукции (закон Ленца), а в 1842 г. (независимо от Дж. Джоуля) – закон теплового действия электрического тока (закон Джоуля-Ленца). Открыл обратимость электрических машин. Изучал зависимость сопротивление металлов от температуры. Работы относятся также к геофизике.

Независимо друг от друга Джоуль и Ленц показали, что при протекании тока, в проводнике выделяется количество теплоты:

(7.7.4)

Если ток изменяется со временем, то

.

Это закон Джоуля–Ленца в интегральной форме.

Отсюда видно, что нагревание происходит за счет работы, совершаемой силами поля над зарядом.

Соотношение (7.7.4) имеет интегральный характер и относится ко всему проводнику с сопротивлением R, по которому течет ток I. Получим закон Джоуля-Ленца в локальной-дифференциальной форме, характеризуя тепловыделение в произвольной точке.

Тепловая мощность тока в элементе проводника Δl, сечением ΔS, объемом равна:

.

Удельная мощность тока

.

Согласно закону Ома в дифференциальной форме . Отсюда закон Джоуля — Ленца в дифференциальной форме характеризующий плотность выделенной энергии:

,

(7.7.5)

Так как выделенная теплота равна работе сил электрического поля

,

то мы можем записать для мощности тока:

.

(7.7.6)

Мощность, выделенная в единице объема проводника .

Приведенные формулы справедливы для однородного участка цепи и для неоднородного.

Наряду с работой тока очень важно отметить мощность тока, так как эта характеристика является ключевой в бытовом использовании электроэнергии (на всех бытовых приборах указано приемлемое напряжение его мощность).

Определение.Мощность – это работа, выполненная за единицу времени (скорость выполнения током работы):

Единица измерения мощности – ватт:

И теперь, используя наши знания о работе тока, мы без труда найдем формулу для мощности тока:

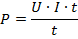
Или же, если использовать другие виды формулы для работы:

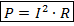
1 ватт определяется как мощность, при которой за 1 секунду времени совершается работа в 1 джоуль. [3] Таким образом, ватт является производной единицей измерения и связан с другими единицами СИ следующими соотношениями:

Вт = Дж / с = кг·м²/с³

Кроме механической (определение которой приведено выше), различают ещё тепловую и электрическую мощность.

в интегральной форме: Q = I 2 × R × t;

в дифференциальной форме: Р_уд = × Е 2 = .

Если в проводнике течет постоянный ток и проводник остается неподвижным, то работа сторонних сил расходуется на его нагревание. Опыт показывает, что в любом проводнике происходит выделение теплоты, равное работе, совершаемой электрическими силами по переносу заряда вдоль проводника. Если на концах участка проводника имеется разность потенциалов , тогда работу по переносу заряда q на этом участке равна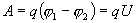

По определению I= q/t. откуда q= I t. Следовательно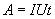

Так как работа идет па нагревание проводника, то выделяющаяся в проводнике теплота Q равна работе электростатических сил

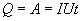
Данное Соотношение выражает закон Джоуля-Ленца в интегральной форме. Введем плотность тепловой мощности 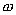, равную энергии выделенной за единицу время прохождения тока в каждой единице объема проводника

где S — поперечное сечение проводника, 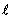— его длина. Используя (1.13) и соотношение 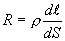, получим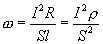

Но 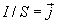— плотность тока, а 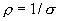, тогда
с учетом закона Ома в дифференциальной форме 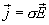, окончательно получаем

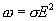Формула выражает закон Джоуля-Ленца в дифференциальной форме: объемная плотность тепловой мощности тока в проводнике равна произведению его удельной электрической проводимости на квадрат напряженности электрического поля.

Не нашли то, что искали? Воспользуйтесь поиском:

Лучшие изречения: Только сон приблежает студента к концу лекции. А чужой храп его отдаляет. 8955 — | 7623 — или читать все.

91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.

Отключите adBlock!
и обновите страницу (F5)
очень нужно