Точки заданы координатами а 2 5

Плоскости проекций V, H, W принимаются за координатные плоскости, а оси проекций X, Y, Z за координатные оси как положительные, так и отрицательные (рис. 10).

Положение точки в пространстве задается тремя координатами – X, Y, Z. Проекции точки задаются двумя координатами: а(х, y), а′(х, z), а′′(y, z).

Зная направление для положительного и отрицательного значений координатных осей, принимая во внимание свойства проекций точки, можно построить проекции точки по координатам. Рассмотрим несколько задач на эту тему.

Задача. Построить проекции точки А(–10; 40; –30) (рис. 10).

Рис. 10. Построение проекций точки А по координатам

Для построения фронтальной проекции а′ точки А справа от точки О на оси Х откладываем значение Х = –10. Вниз от точки О по направлению оси Z откладываем значение Z = –30. Пересечением перпендикуляров из точек а_X и а_Z,восстановленных к соответствующим осям Х и Z, определяем точку а′.

Для построения горизонтальной проекции а точки А по направлению оси Y вниз от точки О откладываем значение y = – 40. Через точку а_Y проводим перпендикуляр до пересечения с линией связи а′а_X. Отмечаем точку а – горизонтальную проекцию точки А. По расположению фронтальной и горизонтальной проекций точки А определяем, что точка А расположена в VΙΙΙ октанте.

Для построения профильной проекции а′′ точки А через ее фронтальную проекцию а′ проводим линию связи а′а_Z и на ней, вправо от точки а_Z, откладываем значение y = 40. Отмечаем точку а′′ – профильную проекцию точки А.

Задача. Построить проекции точек по координатам и указать октант, в котором находится каждая из них.

Исходные данные: А(10; –30; 40), В(70; 50; –10), С(20; 15; 0), D(60; 35; 40), Е(50; –10; –25).

Решение. Порядок выполнения графической части задачи (рис. 11):

1. Проводим оси координат Х, Y, Z. Указываем положительные и отрицательные их направления.

2. Построение точек выполняем в масштабе 1:1.

Точка А (10; –30; 40):

Фронтальную проекцию а′ точки А определяем по координатам Х, Z; по оси Х откладываем 10 мм, по оси Z – 40 мм.

Горизонтальную проекцию а точки А определяем по координатам Х,(–Y), расстояние 30 мм откладываем по оси (–Y), совпадающей с положительным направлением оси Z.

Профильную проекцию а′′ точки А определяем по координатам (–Y), Z. В этом случае расстояние 30 мм откладывается по оси (–Y), совпадающей с положительным направлением оси Х. Следовательно, точка А находится во ΙΙ октанте.

Точка В (70; 50; –10):

Строим фронтальную проекцию b′ (Х = 70; Y = –10) точки А. Расстояние 10 мм нужно отложить на отрицательном направлении оси Z. Уточните: фронтальная b′ и горизонтальная b проекции точки В будут расположены на линии связи ниже оси Х. Профильная проекция b′′ точки В располагается справа от оси Z и ниже оси Х. Анализируя знаки координат (+ + – ) и расположение проекций точки, делаем вывод – точка В находится в ΙV октанте.

Точка С (20; 15; 0):

При построении этой точки очевидно, что фронтальная проекция с′ точки С лежит на оси Х, а ее профильная проекция а′′ лежит на оси Y, совпадающей с отрицательным направлением оси Х. Удаление точки С от плоскости проекций Н равно нулю (y = 0), следовательно, точка С лежит в плоскости Н, на границе Ι и ΙV октантов.

Точка D (60; 35; 40):

Все значения координат положительные, следовательно, точка D находится в Ι октанте.

При отрицательных значениях Y и Z точка располагается в ΙΙΙ октанте. Проекции такой точки располагаются:

— фронтальная проекция е′ точки Е располагается ниже оси Х, слева от оси Y;

— горизонтальная проекция е точки Е располагается выше оси Х, слева от оси Z;

— профильная проекция е′′ точки Е располагается слева от оси Z, ниже оси Х.

Вывод. Положение точки в пространстве вполне определено, если известны три ее координаты или две любые ортогональные проекции. Как следствие из этого – по двум любым заданным ортогональным проекциям точки можно всегда построить недостающую ее третью ортогональную проекцию.

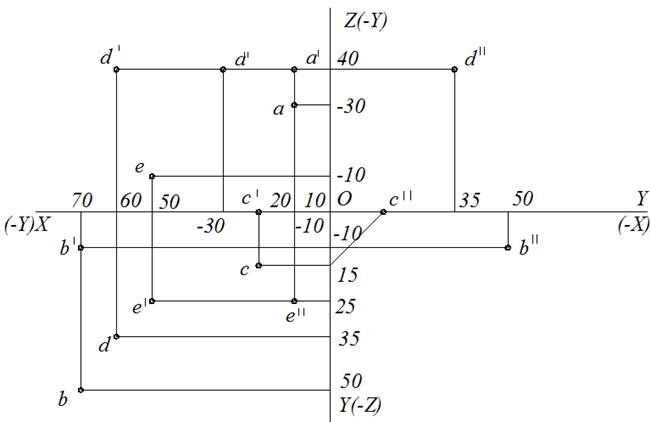
Рис. 11. Построение точек по координатам с указанием октантов

Рассмотри построение точки по двум заданным ортогональным проекциям.

Задача. По двум заданным ортогональным проекциям построить недостающую проекцию точки В (рис. 12).

Рис. 12. Графическое условие задачи

Решение. Анализируем графическое условие задачи: заданы фронтальная и профильная проекции точки В. Это значит, заданы все три координаты точки В. Следовательно, необходимо построить ее горизонтальную проекцию.

Порядок выполнения графической части задачи:

1. Для построения горизонтальной проекции точки В необходимо знать Х_В и У_В. Эти координаты находим на чертеже.

2. Замеряем У_В = b_Z b′′ и откладываем эту координату вдоль линии связи от оси ОХ от точки b_Х.

3. Строим горизонтальную проекцию точки В (рис. 13).

Рис. 13. Построение недостающей проекции точки В

ПРЯМАЯ ЛИНИЯ

При ортогональном проецировании на плоскости проекций прямая линия проецируется в виде прямой. Чтобы построить проекции этой прямой линии, проходящей через заданные точки А и В, нужно построить проекции этих точек и провести прямые линии через их одноименные проекции (рис. 14). Получим:

аb – горизонтальную проекцию отрезка прямой;

а′b′ – фронтальную проекцию отрезка прямой.

Рис. 14. Проекции отрезка прямой, проходящего через две точки

Следы прямой

Прямая пересекает плоскости проекций в точках, которые называются следами прямой.

Точка пересечения прямой N с горизонтальной плоскостью проекций Н (П₁) называется горизонтальным следом N_H.

Точка пересечения прямой с фронтальной плоскостью проекций V (П₂) – фронтальным следом N_V.

Точка пересечения прямой N с профильной плоскостью проекций W (П₃) – профильным следом N_W прямой.

Вывод:

· горизонтальный след прямой – это точка, принадлежащая одновременно данной прямой и лежащая в горизонтальной плоскости проекций H (П₁);

· фронтальный след прямой – это точка, принадлежащая одновременно данной прямой и лежащая во фронтальной плоскости проекций V (П₂);

· профильный след прямой – это точка, принадлежащая одновременно данной прямой и лежащая в профильной плоскости проекций W (П₃).

Задача. Построить точки пересечения прямой N с горизонтальной Н (П₁) и фронтальной V(П₂) плоскостями проекций (рис. 15аб).

Анализируя задачу, приходим к выводу, что необходимо построить горизонтальный и фронтальный следы прямой.

1. Построение фронтального следа N_V.

Необходимо построить точку, принадлежащую прямой N и фронтальной плоскости проекций. Согласно изложенному ранее материалу, горизонтальная проекция искомой точки должна:

– лежать на оси Х;

– принадлежать горизонтальной проекции прямой N.

Порядок выполнения графической части задачи:

1.1. Отмечаем точку пересечения горизонтальной проекции n прямой N с осью Х, получаем точку n_V – горизонтальную проекцию фронтального следа.

1.2. Через точку n_V проводим линию связи перпендикулярно оси Х.

1.3. Находим точку пересечения линии связи с фронтальной проекцией n′ прямой N, получаем точку N_V – фронтальную проекцию фронтального следа. Через эту точку прямая уходит во вторую четверть (рис. 15а) и в третью четверть (рис. 15б).

2. Построение горизонтального следа N_H.

Необходимо построить точку, принадлежащую прямой N и горизонтальной плоскости проекций Н. Согласно изложенному ранее материалу, фронтальная проекция искомой точки должна:

– лежать на оси Х;

– принадлежать фронтальной проекции прямой N.

Порядок выполнения графической части задачи:

2.1. Отмечаем точку пересечения фронтальной проекции n′ прямой N с осью Х, получаем точку n_H – фронтальную проекцию горизонтального следа.

2.2. Через точку n_H проводим линию связи перпендикулярно оси Х.

2.3. Находим точку пересечения линии связи с горизонтальной проекцией n прямой N, получаем фронтальную проекцию фронтального следа. В этой точке прямая пересекает горизонтальную плоскость и уходит в четвертую четверть (рис. 15а,б).

а

б

Рис. 15. Построение следов прямой линии N:

а – прямая уходит во вторую четверть; б – прямая уходит в третью четверть

Данная статья рассматривает понятие проекции точки на прямую (ось). Мы дадим ему определение с использованием поясняющего рисунка; изучим способ определения координат проекции точки на прямую (на плоскости или в трехмерном пространстве); разберем примеры.

Проекция точки на прямую, определение

В статье «Проекция точки на плоскость, координаты» мы упоминали, что проецирование фигуры является обобщенным понятием перпендикулярного или ортогонального проецирования.

Все геометрические фигуры состоят из точек, соответственно проекция этой фигуры есть множество проекций всех ее точек. Поэтому, чтобы иметь возможность спроецировать фигуру на прямую, необходимо получить навык проецирования точки на прямую.

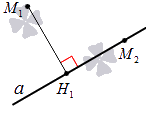
Проекция точки на прямую – это или сама точка, если она принадлежит заданной прямой, или основание перпендикуляра, опущенного из этой точки на заданную прямую.

Рассмотрим рисунок ниже: точка H 1 служит проекцией точки М 1 на прямую a , а точка М 2 , принадлежащая прямой, является проекцией сама себя.

Данное определение верно для случая на плоскости и в трехмерном пространстве.

Чтобы на плоскости получить проекцию точки М 1 на прямую a , проводится прямая b , проходящая через заданную точку M 1 и перпендикулярная прямой a . Таким образом, точка пересечения прямых a и b будет проекцией точки М 1 на прямую a .

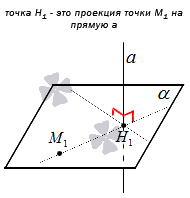
В трехмерном пространстве проекцией точки на прямую будет служить точка пересечения прямой a и плоскости α , проходящей через точку М 1 и перпендикулярной прямой a .

Нахождение координат проекции точки на прямую

Рассмотрим данный вопрос в случаях проецирования на плоскости и в трехмерном пространстве.

Пусть нам заданы прямоугольная система координат O x y , точка М 1 ( x 1 , y 1 ) и прямая a . Необходимо найти координаты проекции точки М 1 на прямую a .

Проложим через заданную точку М 1 ( x 1 , y 1 ) прямую b перпендикулярно прямой a . Точку пересечения маркируем как H 1 . Точка Н 1 будет являться точкой проекции точки М 1 на прямую a .

Из описанного построения можно сформулировать алгоритм, который позволяет находить координаты проекции точки М 1 ( x 1 , y 1 ) на прямую a :

— составляем уравнение прямой (если оно не задано). Для совершения этого действия необходим навык составления основных уравнений на плоскости;

— записываем уравнение прямой b (проходящей через точку М 1 и перпендикулярной прямой a ). Здесь поможет статья об уравнении прямой, проходящей через заданную точку перпендикулярно заданной прямой;

— определяем искомые координаты проекции как координаты точки пересечения прямых a и b . Для этого решаем систему уравнений, составляющие которой – уравнения прямых a и b .

На плоскости O x y заданы точки М 1 ( 1 , 0 ) и прямая a (общее уравнение – 3 x + y + 7 = 0 ). Необходимо определить координаты проекции точки М 1 на прямую a .

Решение

Уравнение заданной прямой известно, поэтому, согласно алгоритму, переходим к шагу записи уравнения прямой b . Прямая b перпендикулярна прямой a , а значит нормальный вектор прямой a служит направляющим вектором прямой b . Тогда направляющий вектор прямой b запишем как b → = ( 3 , 1 ) . Запишем и каноническое уравнение прямой b , поскольку нам также заданы координаты точки М 1 , через которую проходит прямая b :

Заключительным шагом определяем координаты точки пересечения прямых a и b . Перейдем от канонических уравнений прямой b к общему ее уравнению:

x — 1 3 = y 1 ⇔ 1 · ( x — 1 ) = 3 · y ⇔ x — 3 y — 1 = 0

Составим систему уравнений из общих уравнений прямых a и b и решим ее:

3 x + y + 7 = 0 x — 3 y — 1 = 0 ⇔ y = — 3 x — 7 x — 3 y — 1 = 0 ⇔ y = — 3 x — 7 x — 3 · ( — 3 x — 7 ) — 1 = 0 ⇔ ⇔ y = — 3 x — 7 x = — 2 ⇔ y = — 3 · ( — 2 ) — 7 x = — 2 ⇔ y = — 1 x = — 2

В конечном итоге мы получили координаты проекции точки М 1 ( 1 , 0 ) на прямую 3 x + y + 7 = 0 : ( — 2 , — 1 ) .

Ответ: ( — 2 , — 1 ) .

Подробнее рассмотрим случай, когда необходимо определить координаты проекции заданной точки на координатные прямые и параллельные им прямые.

Пусть заданы координатные прямые O x и O y , а также точка М 1 ( x 1 , y 1 ) . Понятно, что проекцией заданной точки на координатную прямую O x вида y = 0 будет точка с координатами ( x 1 , 0 ) . Так и проекция заданной точки на координатную прямую O y будет иметь координаты 0 , y 1 .

Любую произвольную прямую, параллельную оси абсцисс, возможно задать неполным общим уравнением B y + C = 0 ⇔ y = — C B , а прямую, параллельную оси ординат — A x + C = 0 ⇔ x = — C A.

Тогда проекциями точки М 1 ( x 1 , y 1 ) на прямые y = — C B и x = — C A станут точки с координатами x 1 , — C B и — C A , y 1 .

Определите координаты проекции точки М 1 ( 7 , — 5 ) на координатную прямую O y , а также на прямую, параллельную прямой O y 2 y — 3 = 0 .

Решение

Запишем координаты проекции заданной точки на прямую O y : ( 0 , — 5 ) .

Запишем уравнение прямой 2 y — 3 = 0 в виде y = 3 2 . Становится видно, что проекция заданной точки на прямую y = 3 2 будет иметь координаты 7 , 3 2 .

Ответ: ( 0 , — 5 ) и 7 , 3 2 .

Пусть в трехмерном пространстве заданы прямоугольная система координат O x y z , точка М 1 ( x 1 , y 1 , z 1 ) и прямая a . Найдем координаты проекции точки М 1 на прямую a .

Построим плоскость α , проходящую через точку М 1 и перпендикулярную прямой a . Проекцией заданной точки на прямую a станет точка пересечения прямой a и плоскости α . Исходя из этого, приведем алгоритм для нахождения координат проекции точки М 1 ( x 1 , y 1 , z 1 ) на прямую a :

— запишем уравнение прямой а (если оно не задано). Для решения этой задачи необходимо ознакомиться со статьей об уравнениях прямой в пространстве;

— составим уравнение плоскости α , проходящей через точку М 1 и перпендикулярной прямой a (см. статью «Уравнение плоскости, проходящей через заданную точку перпендикулярно заданной прямой»);

— найдем искомые координаты проекции точки М 1 ( x 1 , y 1 , z 1 ) на прямую a – это будут координаты точки пересечения прямой α и плоскости α (в помощь – статья «Координаты точки пересечения прямой и плоскости»).

Задана прямоугольная система координат O x y z , и в ней – точка М 1 ( 0 , 1 , — 1 ) и прямая a . Прямой a соответствуют канонические уравнения вида: x + 2 3 = y — 6 — 4 = z + 1 1 . Определите координаты проекции точки М 1 на прямую a .

Решение

Используем указанный выше алгоритм. Уравнения прямой a известны, поэтому первый шаг алгоритма пропускаем. Запишем уравнение плоскости α . Для этого определим координаты нормального вектора плоскости α . Из заданных канонических уравнений прямой a выделим координаты направляющего вектора этой прямой: ( 3 , — 4 , 1 ) , который будет являться нормальным вектором плоскости α , перпендикулярной прямой a . Тогда n → = ( 3 , — 4 , 1 ) – нормальный вектор плоскости α . Таким образом, уравнение плоскости α будет иметь вид:

3 · ( x — 0 ) — 4 · ( y — 1 ) + 1 · ( z — ( — 1 ) ) = 0 ⇔ 3 x — 4 y + z + 5 = 0

Теперь найдем координаты точки пересечения прямой а и плоскости α, для этого используем два способа:

1. Заданные канонические уравнения позволяют получить уравнения двух пересекающихся плоскостей, определяющих прямую a :

x + 2 3 = y — 6 — 4 = z + 1 1 ⇔ — 4 · ( x + 2 ) = 3 · ( y — 6 ) 1 · ( x + 2 ) = 3 · ( z + 1 ) 1 · ( y — 6 ) = — 4 · ( z + 1 ) ⇔ 4 x + 3 y — 10 = 0 x — 3 z — 1 = 0

Чтобы найти точки пересечения прямой 4 x + 3 y — 10 = 0 x — 3 z — 1 = 0 и плоскости 3 x — 4 y + z + 5 = 0 , решим систему уравнений:

4 x + 3 y — 10 = 0 x — 3 z — 1 = 0 3 x — 4 y + z + 5 = 0 ⇔ 4 x + 3 y = 10 x — 3 z = 1 3 x — 4 y + z = — 5

В данном случае используем метод Крамера, но возможно применить любой удобный:

∆ = 4 3 0 1 0 — 3 3 — 4 1 = — 78 ∆ x = 10 3 0 1 0 — 3 — 5 — 4 1 = — 78 ⇒ x = ∆ x ∆ = — 78 — 78 = 1 ∆ y = 4 10 0 1 1 — 3 3 — 5 1 = — 156 ⇒ y = ∆ y ∆ = — 156 — 78 = 2 ∆ z = 4 3 10 1 0 1 3 — 4 — 5 = 0 ⇒ z = ∆ z ∆ = 0 — 78 = 0

Таким образом, проекцией заданной точки на прямую a является точка c координатами ( 1 , 2 , 0 )

1. На основе заданных канонических уравнений легко записать параметрические уравнения прямой в пространстве:

x + 2 3 = y — 6 — 4 = z + 1 1 ⇔ x = — 2 + 3 · λ y = 6 — 4 · λ z = — 1 + λ

Подставим в уравнение плоскости, имеющее вид 3 x — 4 y + z + 5 = 0 , вместо x , y и z их выражения через параметр:

3 · ( — 2 + 3 · λ ) — 4 · ( 6 — 4 · λ ) + ( — 1 + λ ) + 5 = 0 ⇔ 26 · λ = 0 ⇔ λ = 1

Вычислим искомые координаты точки пересечения прямой a и плоскости α по параметрическим уравнениям прямой a при λ = 1 :

x = — 2 + 3 · 1 y = 6 — 4 · 1 z = — 1 + 1 ⇔ x = 1 y = 2 z = 0

Таким образом, проекция заданной точки на прямую a имеет координаты ( 1 , 2 , 0 )

Ответ: ( 1 , 2 , 0 )

Напоследок отметим, что проекциями точки М 1 ( x 1 , y 1 , z 1 ) на координатные прямые O x , O y и O z буду являться точки с координатами ( x 1 , 0 , 0 ) , ( 0 , y 1 , 0 ) и ( 0 , 0 , z 1 ) соответственно.

Решение задачи по начертательной геометрии — части пространства (Октанты).

Задача

По заданным координатам точек А и В построить три проекции прямой АВ, и определить истинную длину (натуральную величину) отрезков по частям пространства (октантам).

A (50; 80; -10); B (-15; -35; 70).

Задачу по начертательной геометрии необходимо решить на комплексном чертеже.

Решение:

1) По заданным координатам строим проекции точек А и В в 3-ех плоскостях проекций. Соединяем проекции концов отрезка А и В в каждой плоскости, получаем A»B» — фронтальная проекция, A’B’ — горизонтальная проекция, A»’B»’ — профильная проекция отрезка.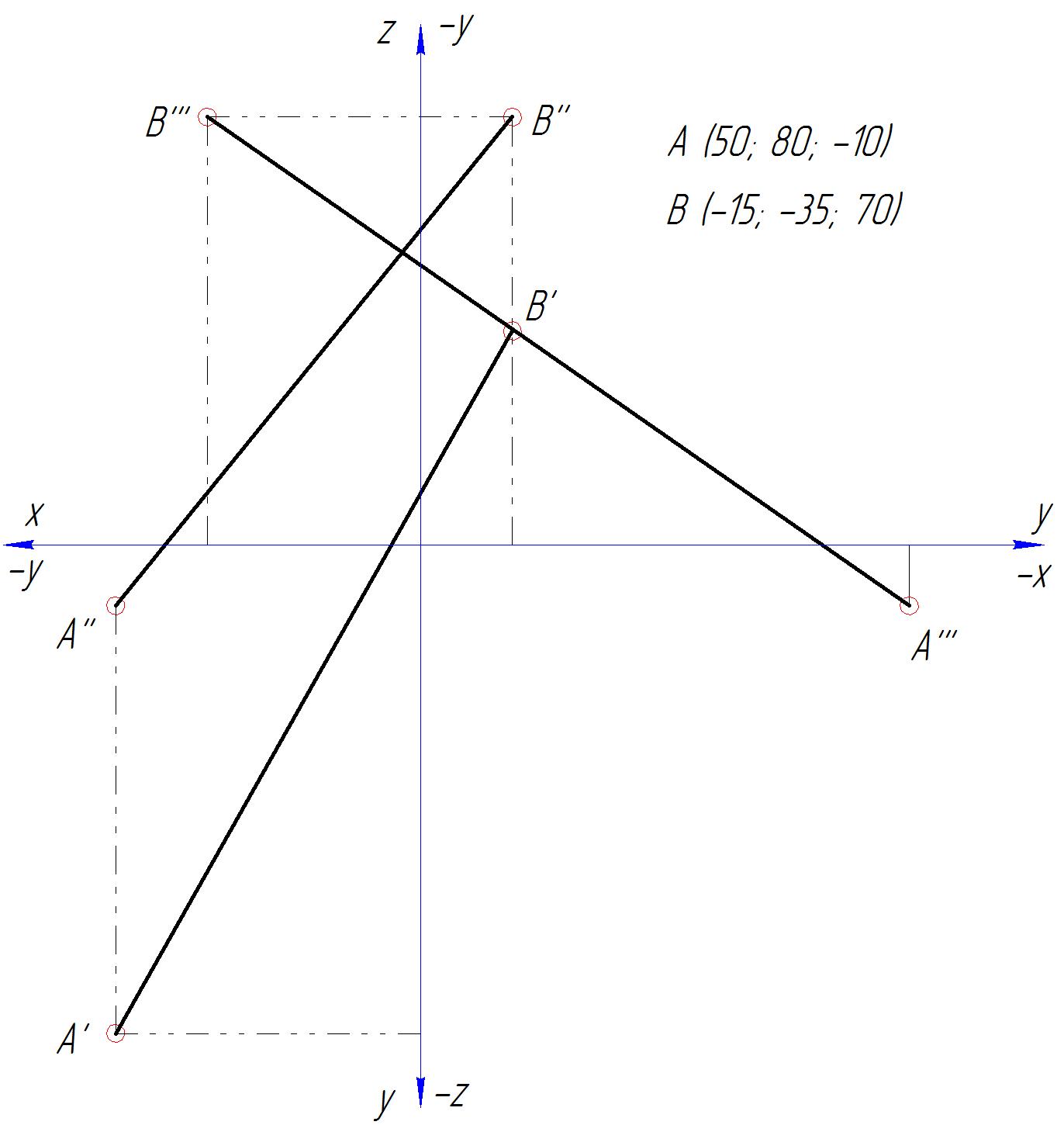

2) Способом прямоугольного треугольника определяем истинную длину всего отрезка |АВ|.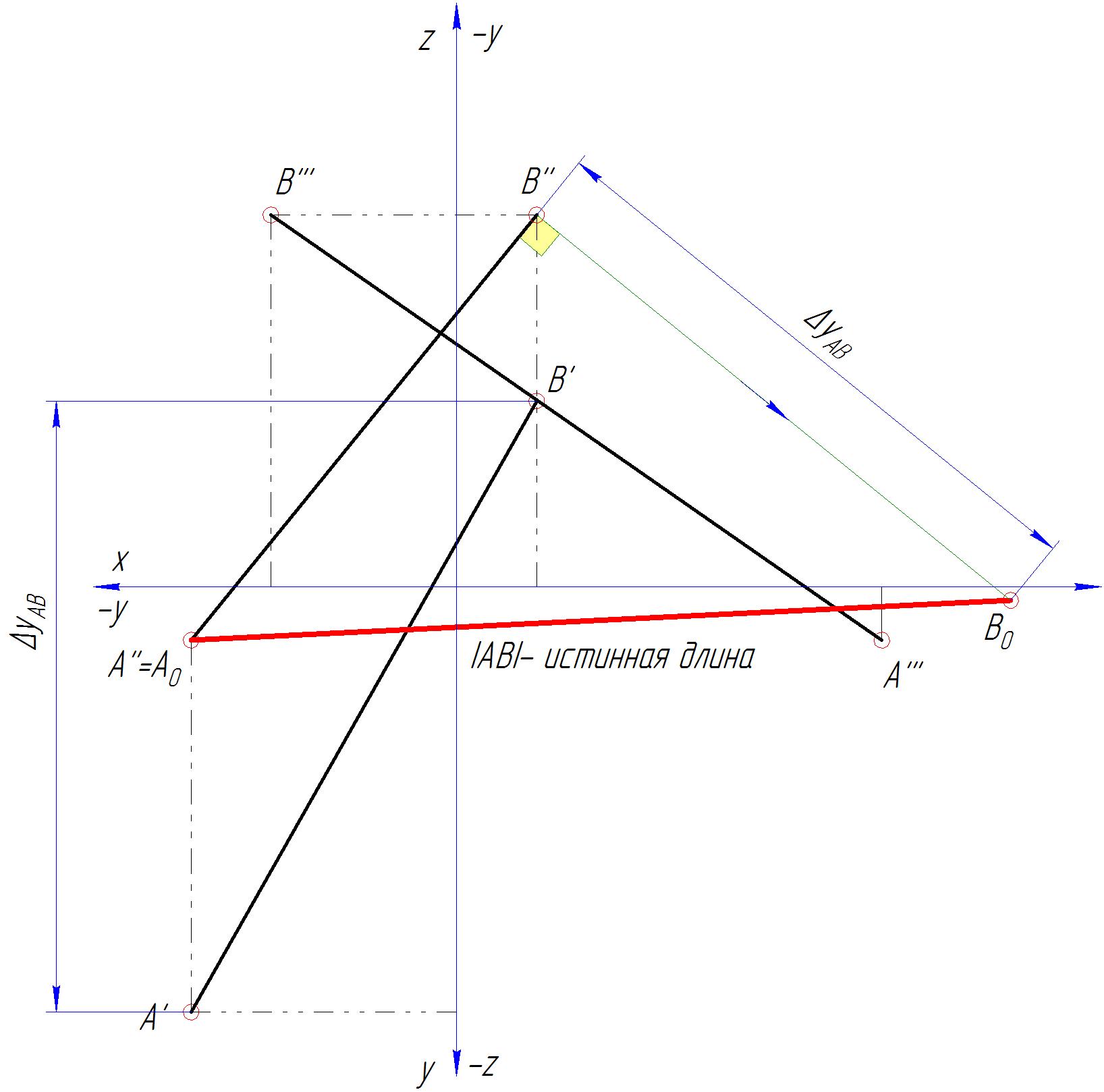

3) Определяем следы отрезка, т.е. точки пересечения прямой с плоскостями проекций — M=M’ горизонтальной, N=N» фронтальной и Р =P»’— профильной плоскостью.

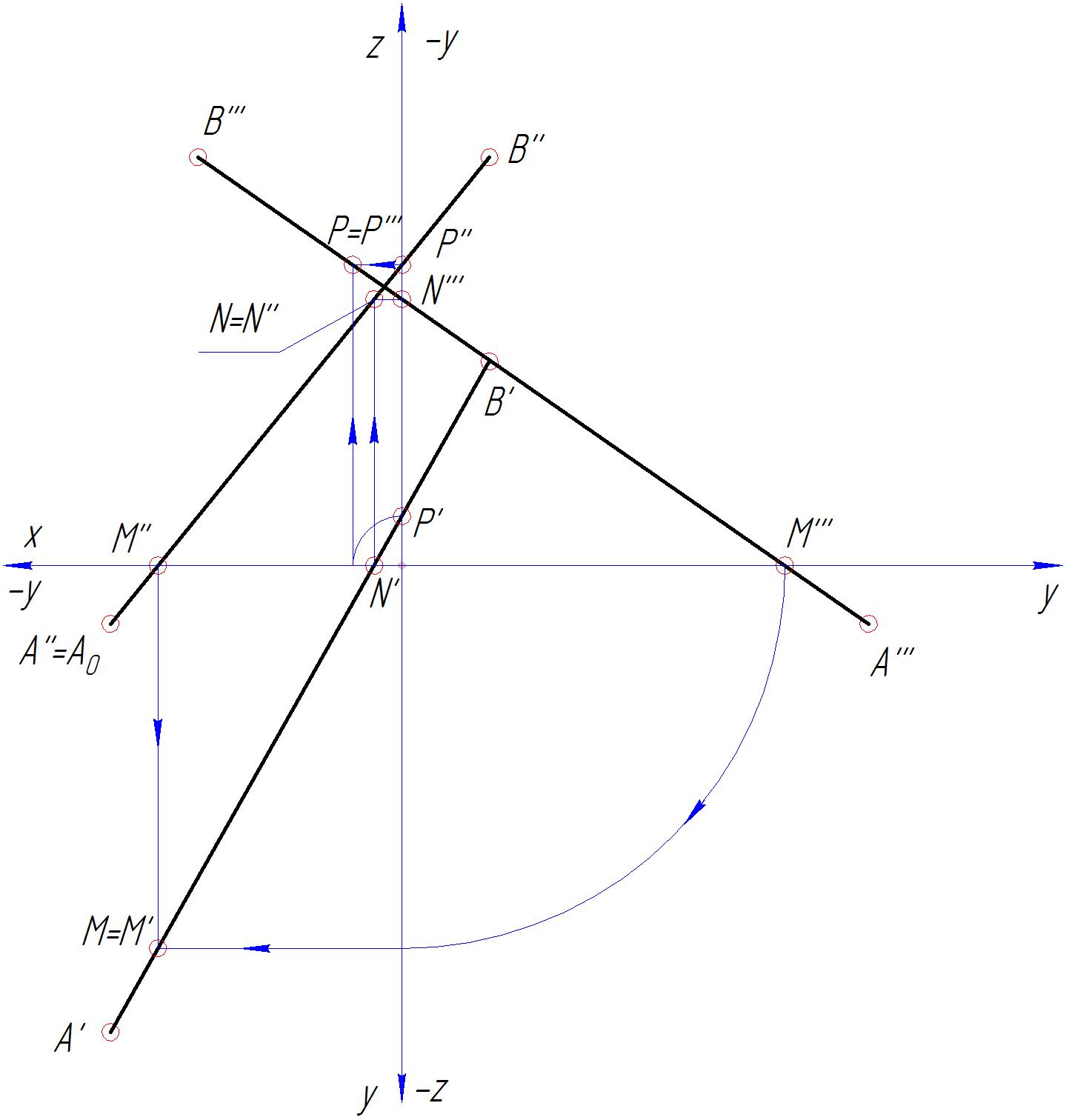
4) Итак, у нас получилось, что отрезок АВ разделен на 4 отрезка: AM, MN, NP и PB, каждый из которых лежит в некотором октанте, и в точках M, N, P переходит в другой октант или часть пространства.

5) Начало отрезка — точка А имеет координаты A (50; 80; -10), x=50 >0, y=80>0 и z 0 или