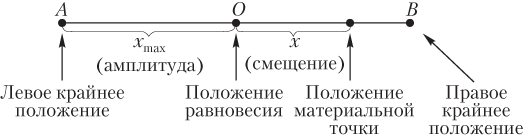Условие задачи:
Материальная точка совершает гармонические колебания. Если при неизменной амплитуде уменьшить частоту колебаний в четыре раза, во сколько раз изменится максимальное значение возвращающей силы, действующей на точку.
Задача №9.1.26 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Решение задачи:
Если материальная точка совершает гармонические колебания, то уравнение этих колебаний можно представить в виде:
В этой формуле (A) — амплитуда колебаний, (omega) — циклическая частота колебаний.
Чтобы найти уравнение ускорения точки при этих колебаниях, нужно дважды взять производную от уравнения колебаний. Сначала возьмем первую производную:
Теперь берем вторую производную:
То есть мы имеем:
Понятно, что максимальное по модулю значение ускорения в таком случае следует искать по формуле:
Циклическая частота колебаний (omega) и частота колебаний (
u) связаны по известной формуле:
Тогда формула (1) примет вид:
Максимальную возвращающую силу (F_<max>) следует определять по формуле (это второй закон Ньютона):
Тогда искомое отношение (frac>>) равно:
Учитывая формулу (2), имеем:
В условии говорится, что частоту колебаний уменьшают в четыре раза, то есть (
u_2=frac<
u_1><4>), поэтому:
Ответ: уменьшится в 16 раз.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
точка совершает гармонические колебания
Точка совершает гармонические колебания, уравнение которых имеет вид х = A sin ωt, где A = 5 см; ω = 2 с. В момент, когда на точку действовала возвращающая сила F = +5 мН, точка обладала потенциальной энергией П = 0,1 мДж. Найти этот момент времени t и соответствующую ему фазу φ колебания.
Точка совершает гармонические колебания с периодом T = 6 с и начальной фазой, равной нулю. Определите, за какое время, считая от начала движения, точка сместится от положения равновесия на половину амплитуды.
За какую часть периода точка, совершающая гармонические колебания, пройдет путь, равный 0,828 А, где А — амплитуда колебаний, если в начальный момент точка находилась в положении равновесия?
Точка совершает гармонические колебания с периодом 2 с. Амплитуда колебаний 10 см. Найти смещение, скорость и ускорение точки спустя 0,2 с после ее прохождения через положение равновесия. Начало колебаний связано с положением равновесия.
Точка совершает гармонические колебания с частотой 10 Гц. В момент, принятый за начальный, точка имела максимальное смещение 1 мм. Написать уравнение колебаний точки и начертить их график.
Точка совершает гармонические колебания с начальной фазой, равной нулю. Найдите период колебаний, если известно, что за время, равное 3 с, считая от начала движения, точка сместилась от положения равновесия на 7/10 амплитуды.
Через какое время от начала движения точка, совершающая гармоническое колебание, сместится от положения равновесия на половину амплитуды? Период колебаний m = 24 с, начальная фаза φ = 0.
Точка совершает гармоническое колебание. Период колебаний Т = 2 с, амплитуда А = 50 мм, начальная фаза φ = 0. Найти скорость v точки в момент времени, когда смещение точки от положения равновесия x = 25 мм.
Точка совершает гармонические колебания. Наибольшее смещение xmax точки равно 10 см, наибольшая скорость max = 20 см/с. Найти угловую частоту ω колебаний и максимальное ускорение
max точки.
Максимальная скорость max точки, совершающей гармонические колебания, равна 10 см/с, максимальное ускорение
max = 100 см/с 2 . Найти угловую частоту ω колебаний, их период Т и амплитуду А. Написать уравнение колебаний, приняв начальную фазу равной нулю.
Точка совершает гармонические колебания по закону x = 3cos(πt/2+π/8), м. Определите: 1) период колебаний, 2) максимальную скорость vmax точки; 3) максимальное ускорение аmаx точки.
Точка совершает гармонические колебания. В некоторый момент времени смещение точки x = 5 см, скорость ее v = 0,2 м/с и ускорение a = ?0,8 м/с 2 . Найти циклическую частоту, период колебаний, фазу и амплитуду колебаний в рассматриваемый момент времени.
Точка совершает гармонические колебания согласно уравнению x = 0,4 sinπt (м). Определить скорость и ускорение точки через 1/6 с от начала колебаний.
За какую часть периода точка, совершающая гармонические колебания, пройдет путь, равный 0,829 А, где А — амплитуда колебаний, если в начальный момент точка находилась в положении равновесия?
Точка совершает гармонические колебания вдоль некоторой прямой с периодом Т = 0,60 с и амплитудой а = 10,0 см. Найти среднюю скорость точки за время, в течение которого она проходит путь а/2: а) из крайнего положения; б) из положения равновесия.
При гармонических колебаниях различные колебательные системы (математический и пружинный маятники) описываются одинаковыми уравнениями. Материальная точка при гармонических колебаниях проходит ряд положений, смещаясь по обе стороны от положения равновесия на равные расстояния.
Смещение материальной точки от положения равновесия характеризует ее положение в пространстве в конкретный момент времени (рис. 10.10). Зависимость смещения (координаты) от времени при гармонических колебаниях описывается уравнениями:
x ( t ) = x max sin ( ω t + φ 0 ) или x ( t ) = x max cos ( ω t + φ 0 ) ,
где x max — максимальное значение смещения материальной точки от положения равновесия ( амплитуда ), x max = A ; φ — фаза колебаний, φ = ω t + φ 0 ; φ 0 — начальная фаза колебаний.
Для упрощения этих уравнений целесообразно пользоваться правилами:
1) если гармонические колебания начинаются из положения равновесия , то для смещения материальной точки выбирают формулу
x ( t ) = x max sin ω t ;
2) если гармонические колебания начинаются из крайнего положения , то для смещения материальной точки выбирают формулу
x ( t ) = x max cos ω t .
Смещение материальной точки:
- в положении равновесия равно нулю: x ( t ) = 0;
- крайнем положении равно максимальному значению — амплитуде: x ( t ) = x max = A .
Скорость материальной точки при гармонических колебаниях изменяется с течением времени также по гармоническому закону; зависимость проекции скорости на координатную ось, выбранную вдоль линии ее движения, от времени описывается уравнениями:
v x ( t ) = v max cos ( ω t + φ 0 ) или v x ( t ) = − v max sin ( ω t + φ 0 ) ,
где v max — максимальное значение проекции скорости ( амплитуда скорости ), v max = ω A ; φ — фаза колебаний, φ = ω t + φ 0 ; φ 0 — начальная фаза колебаний.
Для упрощения этих уравнений целесообразно пользоваться правилами:
1) если гармонические колебания начинаются из положения равновесия , то для проекции скорости выбирают формулу
v x ( t ) = v max cos ω t ;
2) если гармонические колебания начинаются из крайнего положения , то для проекции скорости выбирают формулу
v x ( t ) = − v max sin ω t .
Значение скорости материальной точки:
- в положении равновесия максимально: v ( t ) = v max = ω A ;
- крайнем положении равно нулю: v ( t ) = 0.
Ускорение материальной точки при гармонических колебаниях изменяется с течением времени также по гармоническому закону; зависимость проекции ускорения на координатную ось, направленную в сторону смещения, от времени описывается уравнениями:
a x ( t ) = − a max sin(ω t + φ 0 ) или a x ( t ) = − a max cos(ω t + φ 0 ),
где a max — максимальное значение проекции ускорения ( амплитуда ускорения ), a max = ω 2 A ; φ — фаза колебаний, φ = ω t + φ 0 ; φ 0 — начальная фаза колебаний.
Для упрощения этих уравнений целесообразно пользоваться правилами:
1) если гармонические колебания начинаются из положения равновесия , то для проекции ускорения выбирают формулу
a x ( t ) = − a max sin ω t ;
2) если гармонические колебания начинаются из крайнего положения , то для проекции ускорения выбирают формулу
a x ( t ) = − a max cos ω t .
Значение ускорения материальной точки:
- в положении равновесия равно нулю: a ( t ) = 0;
- крайнем положении значение ускорения максимально: a ( t ) = a max = ω 2 A .
При решении задач на механические гармонические колебания следует помнить, что одно полное колебание происходит за время, равное периоду колебаний; при этом материальная точка проходит ряд последовательных состояний, возвращаясь в исходное положение:
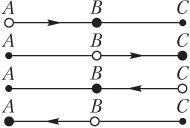
- если колебания начинаются из положения равновесия (рис. 10.11), то она последовательно перемещается из точки A в точку В , затем возвращается в точку A , после чего — в точку C , затем вновь попадает в точку A (в этом случае положением равновесия является точка A );
- если колебания начинаются из крайнего положения (рис. 10.12), то она последовательно перемещается из точки A в точку В , затем — в точку C , после чего возвращается в точку B , затем вновь попадает в точку A (в этом случае положением равновесия является точка B ).
При механических гармонических колебаниях материальная точка:
- за одно полное колебание проходит путь, равный четырем амплитудам:
ее фаза изменяется на величину, равную 2π:
- за n полных колебаний материальная точка проходит путь
ее фаза изменяется на величину
Пример 7. Точка совершает колебания по закону
x ( t ) = 80,0 cos(31,4 t + 62,8),
где x — смещение в сантиметрах; t — время в секундах.
Найти фазу колебаний через 500 мс после начала процесса.
Решение . Фаза гармонических колебаний определяется формулой
где ω — циклическая частота колебаний; t — время; φ 0 — начальная фаза колебаний.
Согласно условию задачи закон изменения фазы колебаний с течением времени имеет следующий вид:
φ( t ) = 31,4 t + 62,8.
Сопоставление с предыдущей формулой дает:
ω = 31,4 рад/с; φ 0 = 62,8 рад.
В указанный момент времени t = 500 мс фаза имеет значение
φ(0,5 с) = 31,4 ⋅ 500 ⋅ 10 −3 + 62,8 = 78,5 рад.
Данное значение фазы получено в Международной системе единиц, т.е. в радианах.
Пример 8. Тело совершает гармонические колебания с частотой 1 Гц и амплитудой 5 см. Рассчитать максимальное значение ускорения данного тела.
Решение . Максимальное значение ускорения определяется формулой
где ω — циклическая частота колебаний; A — амплитуда колебаний.
Амплитуда колебаний задана в условии задачи:
а циклическая частота колебаний определяется формулой
где ν — частота колебаний, ν = 1 Гц.
Подставим выражение для циклической частоты в формулу для вычисления максимального ускорения:
Вычислим, для удобства считая π 2 ≈ 10:
a max ≈ 4 ⋅ 10 ⋅ 1 ⋅ 5 ⋅ 10 −2 = 2 м/с 2 .
Максимальное значение ускорения тела при гармонических колебаниях с указанными характеристиками составляет 2 м/с 2 .
Пример 9. Материальная точка совершает гармонические колебания с периодом 24 с. Найти минимальный интервал времени, за который точка смещается из положения равновесия на половину амплитуды.
Решение . Материальная точка начинает движение из положения равновесия. В этом случае смещение материальной точки от положения равновесия описывается законом
x ( t ) = x max sin ω t ,
где x max — максимальное значение смещения точки от положения равновесия (амплитуда гармонических колебаний), x max = A ; ω — циклическая частота колебаний; начальная фаза колебаний при таком выборе уравнения равна нулю.
В начальный момент времени t = 0 смещение материальной точки от положения равновесия также равно нулю: x (0) = 0.
Запишем данное уравнение для момента времени t = τ, когда смещение составляет половину амплитуды:
x ( τ ) = x max sin ω τ = x max 2 .
Преобразование уравнения к виду
позволяет найти минимальное значение произведения:
ω τ = arccos ( 1 / 2 ) = π / 6 .
С учетом равенства
искомый момент времени составляет
τ = T 12 = 24 12 = 2,0 с.
Следовательно, смещение материальной точки от положения равновесия на половину амплитуды произойдет через минимальный интервал времени, равный 2,0 с.