Содержание
Комбинаторика и вероятность
Ниже вы найдете основные формулы Excel, которые могут применяться при решении вероятностных задач и задач по комбинаторике.
| ЧИСЛКОМБ / COMBIN |
Выдает случайное число в интервале от 0 до 1 (равномерно распределенное).
Выдает случайное число в заданном интервале.
Вычисляет отдельное значение биномиального распределения.
Определяет гипергеометрическое распределение.
Вычисляет значение нормальной функции распределения.
Выдает обратное нормальное распределение.
Выдает стандартное нормальное интегральное распределение.
Выдает обратное значение стандартного нормального распределения.
Определяет вероятность того, что значение из диапазона находится внутри заданных пределов.
Математическая статистика
При решении задач по математической статистике можно использовать те формулы, что перечислены выше, а также следующие (сгруппированы для удобства: обработка выборки, разные распределения, остальные формулы):
Обработка выборки: формулы Excel
Вычисляет среднее абсолютных значений отклонений точек данных от среднего.
Вычисляет среднее арифметическое аргументов.
Вычисляет среднее геометрическое.
Вычисляет среднее гармоническое.
Определяет эксцесс множества данных.
Находит медиану заданных чисел.
Определяет значение моды множества данных.
Определяет квартиль множества данных.
Определяет асимметрию распределения.
Оценивает стандартное отклонение по выборке.
Оценивает дисперсию по выборке.
Законы распределений: формулы Excel
Определяет интегральную функцию плотности бета-вероятности.
Определяет обратную функцию к интегральной функции плотности бета-вероятности.
Вычисляет одностороннюю вероятность распределения хи-квадрат.
Вычисляет обратное значение односторонней вероятности распределения хи-квадрат.
Находит экспоненциальное распределение.
Находит F-распределение вероятности.
Определяет обратное значение для F-распределения вероятности.
Находит преобразование Фишера.
Находит обратное преобразование Фишера.
Находит обратное гамма-распределение.
Выдает распределение Пуассона.
Выдает t-распределение Стьюдента.
Выдает обратное t-распределение Стьюдента.
Выдает распределение Вейбулла.
Другое (корреляция, регрессия и т.п.)
Определяет доверительный интервал для среднего значения по генеральной совокупности.
Находит коэффициент корреляции между двумя множествами данных.
Подсчитывает количество чисел в списке аргументов.
Подсчитывает количество непустых ячеек, удовлетворяющих заданному условию внутри диапазона.
Определяет ковариацию, то есть среднее произведений отклонений для каждой пары точек.
Вычисляет значение линейного тренда.
Находит параметры линейного тренда.
Определяет коэффициент корреляции Пирсона.
Справочный файл по формулам Excel
Нужна шпаргалка по функциям Excel под рукой? Скачивайте файл: Математические и статистические формулы Excel
Полезные ссылки
А если у вас есть задачи, которые надо срочно сделать, а времени нет? Можете поискать готовые решения в решебнике:
Пример 4.В партии 20 изделий, из них 5 бракованных. Найти вероятность того, что в выборке из 4 изделий ровно одно бракованное.
Решение. В данной задаче, прежде всего, определим значения параметров: число_успехов_ в_ выборке = 1; размер_ выборки = 4; число_ успехов_ в_ совокупности = 5; размер_ совокупности = 20.
Искомую вероятность можно рассчитать с помощью функции =ГИПЕРГЕОМЕТ(1; 4; 5; 20), которая дает значение 0,4696.
Если производится несколько испытаний, причем вероятность события А в каждом испытании не зависит от исходов других испытаний, то такие испытания называют независимыми относительно событияА.
Пусть производится n независимых испытаний, в каждом из которых событие А может появиться либо не появиться. Вероятность события А в каждом испытании одна и та же, а именно равна р. Следовательно, вероятность ненаступления события А в каждом испытании также постоянна и равна q = 1 – р.
Вероятность того, что при n повторных независимых испытаниях событие А осуществится ровно k раз вычисляется по формуле Бернулли: 
.
Для нахождения наиболее вероятного числа успехов k по заданным n и р можно воспользоваться неравенствами np – q £ k£ np + p или правилом: если число np + p не целое, то k равно целой части этого числа.
В случае, если n велико, р мало, а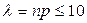 
, используют асимптотическую формулу Пуассона вычисления вероятности наступления события А ровно k раз при n повторных независимых испытаниях: 
.
Пример 5. Вероятность того, что расход электроэнергии на протяжении одних суток не превысит установленной нормы, равна р = 0,75. Найти вероятность того, что в ближайшие 6 суток расход электроэнергии в течение 4 суток не превысит нормы.
Решение. Вероятность нормального расхода электроэнергии на протяжении каждых из 6 суток постоянна и равна p = 0,75. Следовательно, вероятность перерасхода электроэнергии в каждые сутки также постоянна и равна q = 1— р = 1 — 0,75 = 0,25. Искомая вероятность по формуле Бернулли равна 
= 0,297. Для вычисления в Excel используем формулу =БИНОМРАСП(4; 6; 0,75; 0), которая дает значение 0,297. При этом определены следующие значения параметров: число_ успехов = 4; число_ испытаний = 6; вероятность_ успеха = 0,75; интегральная = 0. Подробно с синтаксисом функции БИНОМРАСП можно ознакомиться с помощью справки.
Пример 6. Телефонная станция обслуживает 400 абонентов. Для каждого абонента вероятность того, что в течение часа он позвонит на станцию, равна 0,01. Найти вероятность, что в течение часа ровно 5 абонентов позвонят на станцию.
Решение.Так как р = 0,01 мало и n = 400 велико, то будем пользоваться приближенной формулой Пуассона при l = 400 × 0,01 = 4. Тогда Р400(5) » 
» 0,156293. Для вычисления в Excel используем формулу =ПУАССОН(5; 4; 0), которая дает значение 0,156293. При этом определены следующие значения параметров: количество_ событий = 5; среднее(λ) = 4; интегральная = 0. Подробно с синтаксисом функции ПУАССОН можно ознакомиться в справке.
В случае, когда число повторных испытаний большое и формула Бернулли неприменима, используют формулы Лапласа.
Локальная теорема Лапласа. Если вероятность р появления события А в каждом испытании постоянна и отлична от нуля и единицы, то вероятность 
того, что событие А появится в n испытаниях ровно k раз, приближенно равна (тем точнее, чем больше n) значению функции 
, где 
.
Имеются таблицы, в которых помещены значения функции 
.
Интегральная теорема Лапласа. Если вероятность р наступления события А в каждом испытании постоянна и отлична от нуля и единицы, то вероятность 
того, что событие А появится в n испытаниях от k1 до k2 раз, приближенно равна определенному интегралу:
, где 
.
При решении задач, требующих применения интегральной теоремы Лапласа, пользуются специальными таблицами для интеграла 
, тогда 
.
Пример 7. Найти вероятность того, что событие А наступит ровно 80 раз в 400 испытаниях, если вероятность появления этого события в каждом испытании равна 0,2.
Решение. По условию n = 400; k = 80; р = 0,2; q = 0,8. Воспользуемся асимптотической формулой Лапласа: 
, 
, 
. Для вычисления в Excel используем формулу =НОРМРАСП(80; 80; 8; 0), которая дает значение 0,04986. При этом определены следующие значения параметров: k = 80; среднее= np = 80; стандартное_откл =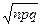 
= 
= 8, интегральная = 0. Подробно с синтаксисом функции НОРМРАСП можно ознакомиться с помощью справки.
Пример 8. Вероятность того, что деталь не прошла проверку ОТК, равна 0,2. Найти вероятность того, что среди 400 случайно отобранных деталей окажется непроверенных от 70 до 100 деталей.
Решение.Воспользуемся интегральной формулой Лапласа: n = 400; k1= 70; k2=100; р = 0,2; q = 0,8; 
. Так как функция 
является нечетной, то P400(70; 100) = Ф(2,5)+ + Ф(1,25) = 0,4938 + 0,3944 = 0,8882.
Для вычисления в Excel используем формулу нормального распределения =НОРМРАСП(100; 80; 8; 1) — НОРМРАСП(70; 80; 8; 1), которая дает значение 0,8882. При этом параметр интегральная = 1, остальные значения параметров определяются аналогично примеру, рассмотренному выше.
В этой статье описаны синтаксис формулы и использование функции ВЕРОЯТНОСТЬ в Microsoft Excel.
Описание
Возвращает вероятность того, что значение из интервала находится внутри заданных пределов. Если верхний_предел не задан, то возвращается вероятность того, что значения в аргументе x_интервал равняются значению аргумента нижний_предел.
Синтаксис
Аргументы функции ВЕРОЯТНОСТЬ описаны ниже.
x_интервал Обязательный. Диапазон числовых значений x, с которыми связаны вероятности.
Интервал_вероятностей Обязательный. Множество вероятностей, соответствующих значениям в аргументе "x_интервал".
Нижний_предел Необязательный. Нижняя граница значения, для которого вычисляется вероятность.
Верхний_предел Необязательный. Верхняя граница значения, для которого вычисляется вероятность.
Замечания
Если любое значение в аргументе интервал_вероятностей меньше 0 или если какое-либо значение в аргументе интервал_вероятностей больше 1, то функция ВЕРОЯТНОСТЬ возвращает значение ошибки #ЧИСЛО!.
Если сумма значений в аргументе интервал_вероятностей не равна 1, функция ВЕРОЯТНОСТЬ возвращает значение ошибки #ЧИСЛО!.
Если верхний_предел опущен, то функция ВЕРОЯТНОСТЬ возвращает вероятность равенства значению аргумента нижний_предел.
Если x_интервал и интервал_вероятностей содержат различное количество точек данных, то функция ВЕРОЯТНОСТЬ возвращает значение ошибки #Н/Д.
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.