Так как комплексное число представлено в алгебраической форме, а выполнять возведение в степень комплексного числа удобно в тригонометрической форме, то сначала выполним перевод из алгебраической формы в тригонометрическую.
Записываем число в тригонометрической форме:
Находим третью степень числа:
$$ z^3 = 2^3(cos (3 cdot frac<pi><3>)+isin (3 cdot frac<pi><3>)) = 8 (cos pi + isin pi) $$
Приводим назад к алгебраической форме:
$$ z^3 = 8 (-1 + i cdot 0) = 8 cdot (-1+0) = -8 $$
Возведение в комплексную степень комплексного числа — это обобщение операции возведения в степень для комплексных чисел .
Так как определение опирается на логарифм комплексного числа, который является многозначной аналитической функцией, то и функция возведения в комплексную степень — многозначная.
Содержание
[править] Обозначения
x1 — действительная часть (абсцисса) первого числа;
y1 — мнимая часть (ордината) первого числа;
x2 — действительная часть (абсцисса) второго числа;
y2 — мнимая часть (ордината) второго числа;
x1+iy1 — первое комплексное число — основание степени;
x2+iy2 — второе комплексное число — показатель степени;
lnx — натуральный логарифм вещественного числа;
Ln(x+iy) — комплексный натуральный логарифм.
[править] Формула
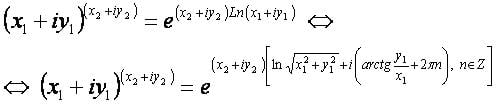
[править] Примеры

[править] Другие операции
- сложение чисел;
- вычитание чисел;
- умножение чисел;
- деление чисел;
- обращение числа;
- возведение в степень;
- извлечение квадратного корня;
- извлечение кубического корня;
- извлечение корня n-ой степени;
- логарифмирование числа;
- возведение в комплексную степень;
- взятие комплексно сопряжённого числа;
- сложение комплексно сопряжённых чисел;
- вычитание комплексно сопряжённых чисел;
- умножение комплексно сопряжённых чисел;
- деление комплексно сопряжённых чисел;
- обращение комплексно сопряжённого числа.
[править] Другие понятия
[править] Литература
- Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. М.: Наука, 1970, стр.623.
[править] Ссылки
Персональные инструменты
Пространства имён
Варианты
Просмотры
Действия
Поиск
Навигация
Инструменты
- Последнее изменение этой страницы: 00:54, 4 января 2018.
- К этой странице обращались 17 511 раз.
Текст страницы доступен по условиям лицензии GNU Free Documentation License. Материалы могут быть скопированы при условии указания активной ссылки на источник копирования в теле статьи (на той же странице). В отдельных случаях могут действовать условия лицензии Creative Commons Attribution-ShareAlike (CC BY-SA 3.0), информацию об этом можно просмотреть на странице обсуждения или в истории правок. В частности, условия лицензии CC BY-SA 3.0 действуют в отношении статей, перенесенных из Википедии (указание на факт переноса всегда есть в истории правок статьи).
- Политика конфиденциальности
- Описание Циклопедии
- Отказ от ответственности
3.1. Натуральная степень комплексного числа
n-й натуральной степенью комплексного числа z называется комплексное число, полученное в результате умножения числа z на себя n раз:
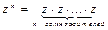 .
.
n-ю степень числа z обозначают z n .
Число z называется основанием степени, а натуральное число n – показателем степени.
n-я степень комплексного числа, записанного в тригонометрической форме
z = r×(cos j + i×sin j),
вычисляется по формуле Муавра:
z n = r n ×(cos n×j + i×sin n×j).
Замечание. Наряду с алгебраической и тригонометрической формами представления к.ч. часто используется так называемая показательная (экспоненциальная) форма. Она основана на формуле Эйлера
 .
.
Показательной (экспоненциальной) формой представления к.ч. называется выражение
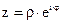 ,
,
где r – модуль к.ч., а j = arg z – главное значение аргумента к.ч.
3.2. Корень n-й степени из комплексного числа
Под корнем n-й степени из к. ч. z понимается множество к. ч., являющихся решениями уравнения
Корень n-й степени из комплексного числа z обозначается символом 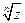 .
.
Все корни n-й степени из комплексного числа z, заданного в тригонометрической форме
z = r×(cos j + i×sin j),
вычисляются по формуле
 ,
,
Геометрически все корни n-й степени из к. ч. z = r×(cos j + i×sin j) изображаются точками, лежащими на окружности с центром в начале координат, радиус которой равен nÖr, а центральные углы между радиусами, проведенными в соседние точки, равны 2p/n.
Пример. Вычислить корни четвертой степени из числа –1.
Решение. Число (–1) в тригонометрической форме может быть записано так: – 1 = 1 × (cos p + i×sin p).
Корни четвертой степени из числа (–1) – это комплексные числа
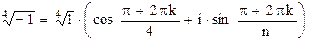 ,
,
где k=0, 1, 2, 3, т.е. комплексные числа
 ,
, 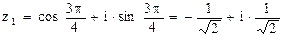 ,
,
 ,
,  .
.
Аналогичным образом в множестве комплексных чисел можно вычислить корень n-й степени из любого действительного числа. При этом хотя бы один корень из положительного действительного числа будет действительным.
Вариант в каждой группе соответствует алфавитному списку группы по порядку нумерации. К ЭКЗАМЕНУ.
Сдать 2 октября в тетрадке отдельной.
Индивидуальное домашнее задание по теме «Комплексные числа»
- Вычислить число
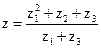 .
.
- Построить на комплексной плоскости числа
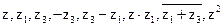 .
.
- Представить в показательной, экспоненциальной и тригонометрической форме заданные комплексные числа, изобразить их на комплексной плоскости.
- Решить уравнение, корни изобразить на комплексной плоскости.

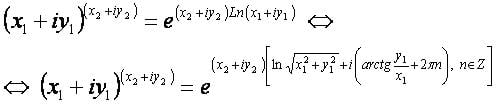


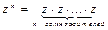 .
. .
.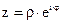 ,
,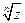 .
. ,
,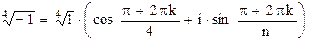 ,
, ,
, 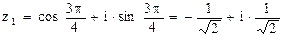 ,
, ,
,  .
.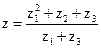 .
.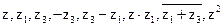 .
.