Связь мат ожидания и дисперсии

Пусть мы измеряем случайную величину раз, например, десять раз измеряем скорость ветра и хотим найти среднее значение. Как связано среднее значение с функцией распределения?

Будем кидать игральный кубик большое количество раз. Количество очков, которое выпадет на кубике при каждом броске, является случайной величиной и может принимать любые натуральные значения от 1 до 6. Среднее арифметическое выпавших очков, подсчитанных за все броски кубика, тоже является случайной величиной, однако при больших оно стремится ко вполне конкретному числу – математическому ожиданию . В данном случае

Каким образом получилась эта величина? Пусть в испытаниях 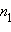раз выпало 1 очко, 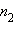раз – 2 очка и так далее. Тогда 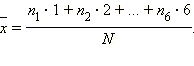При количество исходов, в которых выпало одно очко, 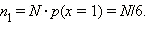Аналогично, 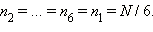Отсюда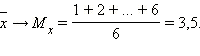

Предположим теперь, что мы знаем закон распределения случайной величины , то есть знаем, что случайная величина может принимать значения с вероятностями Математическое ожидание случайной величины равно

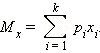Математическое ожидание случайной величины часто обозначается как . Записи и эквивалентны.

Найти математическое ожидание числа очков, которые выбьет первый стрелок в предыдущем примере.

Закон распределения рассматриваемой случайной величины может быть задан следующей таблицей:

Другими словами, вероятность ₁ того, что случайная величина окажется меньшей _1/2, и вероятность ₂ того, что случайная величина окажется большей _1/2, одинаковы и равны 1/2. Медиана определяется однозначно не для всех распределений.

Вернёмся к случайной величине , которая может принимать значения с вероятностями

	Значит, 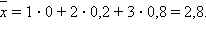Математическое ожидание не всегда является разумной оценкой какой-нибудь случайной величины. Так, для оценки средней заработной платы разумнее использовать понятие медианы, то есть такой величины, что количество людей, получающих меньшую, чем медиана, зарплату и большую, совпадают. Медианой случайной величины называют число 1/2 такое, что

Дисперсией случайной величины называется среднее значение квадрата отклонения случайной величины от её математического ожидания:

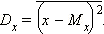Используя вероятности того, что величина принимает значения , эту формулу можно переписать следующим образом:

Среднеквадратическим отклонением случайной величины называется корень квадратный из дисперсии этой величины:

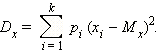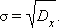В условиях предыдущего примера вычислить дисперсию и среднеквадратическое отклонение случайной величины .

Имеем: .

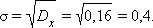Найти распределение вероятности числа очков, выпавших на кубике с первого броска, медиану, математическое ожидание, дисперсию и среднеквадратичное отклонение.

Выпадение любой грани равновероятно, так что распределение будет выглядеть так:

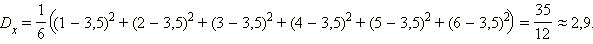Среднеквадратичное отклонение 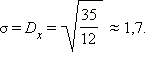Видно, что отклонение величины от среднего значения очень велико.

Свойства математического ожидания Математическое ожидание суммы независимых случайных величин равно сумме их математических ожиданий: Математическое ожидание произведения независимых случайных величин равно произведению их математических ожиданий:

Найти математическое ожидание суммы и произведения очков, выпавшей на двух кубиках.

В примере 3 мы нашли, что для одного кубика Значит, для двух кубиков

Свойства дисперсии Дисперсия суммы независимых случайных величин равно сумме дисперсий:

Найти математическое ожидание и дисперсию суммы очков, выпавших при бросании кубика раз.

Случайный процесс можно представить как сумму единичных бросков. Для единичного броска

Пусть за бросков на кубике выпало очков. Тогда

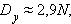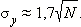Если – среднее количество очков, выпавших на кубике за бросков: 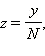то:

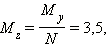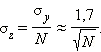Этот результат верен не только для бросков кубика. Он во многих случаях определяет точность измерения математического ожидания опытным путем. Видно, что при увеличении количества измерений разброс значений вокруг среднего, то есть среднеквадратичное отклонение, уменьшается пропорционально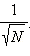

Дисперсия случайной величины связана с математическим ожиданием квадрата этой случайной величины следующим соотношением:

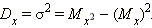Действительно,

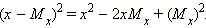Найдём математические ожидания обеих частей этого равенства. По определению, 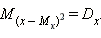Математическое же ожидание правой части равенства по свойству математических ожиданий равно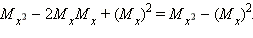

Математическим ожиданием дискретной случайной величины называется сумма вида

Свойства математического ожидания:

1. M(CX)= СМ(Х); М(С) = С, где С-произвольная постоянная величина.

2. , если —

взаимно независимые случайные величины.

3. .

Математическое ожидание характеризует среднее значение случайной величины.

Рассеяние случайной величины около среднего значения характеризуют дисперсия и среднее квадратичное отклонение.

Дисперсией случайной величины X называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания:

Дисперсию целесообразно вычислять по формуле

D(X) = М(Х 2 ) — (М(Х)) 2 .

1. D(CX)= С 2 D(Х); D(С) = 0, где С-произвольная постоянная величина.

2. , если — взаимно независимые случайные величины.

3. — среднеквадратичное отклонение

125. Даны законы распределения двух независимых случайных величин:

X
P	0,4	0,2	0,1	0,3

Y
P	0,5	0,2	0,3

3) MZ, DZ, где Z = 2Х + ЗY

126. Задан ряд распределения:

X
P	0,4	0,2	0,2	0,05	0,1	0,05

Найти М(Х), D(Х) и М(2Х 2 + 3).

127. Даны законы распределения независимых случайньх независимых величин:

X	-4
P	0,1	0,5	0,4

Y
P	0,5	0,5

Найти M(Z) и D(Z), если Z = (X + У)/2.

128. В экзаменационном билете три задачи. Вероятность того, что студент правильно решит первую задачу, равна 0,9, вторую – 0,8, третью – 0,7. Пусть X – число правильно решенных задач. Определить числовые характеристики случайной величины: математическое ожидание, дисперсию и среднее квадратическое отклонение.

129. С целью привлечения покупателей компания «Кока-кола» проводит конкурс, согласно которому каждая десятая бутылка напитка, выпущенная фирмой, является призовой. Составить закон распределения числа призовых из четырех приобретенных покупателем бутылок. Найти математическое ожидание и дисперсию этой случайной величины.

130. В партии из 8 деталей 6 деталей – стандартные. Наугад отбираются две детали.Составить закон распределения случайной величины, равной числу стандартных деталей среди отобранных. Найти ее математическое ожидание, дисперсию.

131. Вероятность наличия нужной книги для первой библиотеки равна 0,2; для второй, третьей и четвертой соответственно 0,2, 0,4 и 0,5. Составить закон распределения числа библиотек, которые последовательно посещает студент в поисках нужной книги. Найти математическое ожидание и дисперсию этой случайной величины.

132. Ткачиха обслуживает 3 станка. Вероятности того, что в течение часа станок не потребует внимания, равны соответственно 0,9; 0,8; 0,7. Составить закон распределения для числа станков, потребовавших внимания в течение часа. Найти математическое ожидание и дисперсию этой случайной величины.

133. Молодого человека пригласили на день рождения. Он помнил номер дома, но забыл номер квартиры, помня лишь, что номер однозначный и нечетный. Составить закон распределения числа посещенных квартир для отыскания нужной. Найти математическое ожидание и дисперсию этой случайной величины.

134. Устройство состоит из трех независимо работающих приборов. Вероятности отказа приборов 0,3; 0,64; 0,5.Cоставить закон распределения числа отказавших приборов. Найти математическое ожидание и дисперсию.

135. Фирма имеет 4 грузовых автомобиля. Вероятность выхода на линию каждого автомобиля равна 0,8. Составить закон распределения случайной величины, равной числу автомобилей, которые выйдут на линию в произвольно выбранный день. Найти математическое ожидание и дисперсию этой случайной величины.

136. Охотник выстрелил три раза по удаляющейся цели. Вероятность попадания в нее при первом выстреле равна 0,8, а для каждого последующего выстрела уменьшается на 0,1.Составить закон распределения случайной величины, равной числу попаданий в цель. Найти математическое ожидание и дисперсию этой случайной величины.

137. Вероятность выигрыша по одному билету лотереи равна 0,05. Найти математическое ожидание M(2X-0,5), если случайная величина Xравна числу выигрышных билетов среди 15 купленных.

138. Ветеринар в зоопарке обследует 5 жирафов. Вероятность того, что рост жирафа будет больше 6 метров, равна 0,1. Найти дисперсию D(2X+ 4), если случайная величина Xравна числу обследованных жирафов с ростом более 6 метров.

139. Два консервных завода поставляют продукцию в ма­газин в пропорции 2:3. Доля продукции высшего качества на первом заводе составляет 90%, а на втором — 80%. В магазине куплено 3 банки консервов. Найти математическое ожидание и среднее квадратичное отклонение числа банок с продукцией высшего качества.

140. Два товароведа проверяют партию изделий. Произ­водительность их труда соотносится как 5:4. Вероятность определения брака первым товароведом составляет 85%, вторым — 90%. Из проверенных изделий отбирают четыре. Найти а) математическое ожидание и б) дисперсию числа год­ных изделий среди отобранных.

141. В магазин поступили электролампы с трех заводов в пропорции 2:3:5. Доля брака в продукции первого завода — 5%, второго — 2%, третьего — 3%. Покупатель приобрел 3 лампочки. Найти а) математическое ожидание и б) среднее квадратичное отклонение числа качественных лампочек среди купленных.

142. Стороны прямоугольного участка X и У в результате погрешностей измерения оказываются случайными величина­ми с такими распределениями:

X	19,5	19,7	20,2
P	0,2	0,05	0,7	0,05

Y	29,5	29,8	30,1
P	0,15	0,15	0,65	0,05

Найти математическое ожидание площади участка, если из­вестно, что измерения проводились независимыми способами.

Не нашли то, что искали? Воспользуйтесь поиском:

Лучшие изречения: Только сон приблежает студента к концу лекции. А чужой храп его отдаляет. 8945 — | 7615 — или читать все.

91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.

Отключите adBlock!
и обновите страницу (F5)
очень нужно

Среди характеристик случайной величины важное значение имеют математическое ожидание и дисперсия. Математическое ожидание это одна из форм представления среднего значения случайной величины, она относится к характеристикам положения, которые являются характерными точками распределения.

Определение 3.7. Математическим ожиданием дискретной случайной величины называется сумма произведений возможных значений случайной величины на вероятности этих значений

Формула (3.6) дает основание трактовать математическое ожидание как средневзвешенное значение случайной величины, для которого вероятности являются весовыми характеристиками соответствующих значений случайной величины.

Замечание. Если случайная величина Z является функцией некоторой случайной величины X. Z = ф(Х), то ее математическое ожидание определяется формулой

Если все значения случайной величины равновероятны, тор .= /п, тогда из формулы (3.6) следует, что

т.е. математическое ожидание в этом случае равно среднему арифметическому всех значений случайной величины.

Пример 3.2. Найти математическое ожидание случайной величины X, зная закон ее распределения:

При определении математического ожидания непрерывной случайной величины суммирование заменяется интегрированием.

Определение 3.8. Математическим ожиданием непрерывной случайной величины X называется интеграл

где 1(х) — плотность распределения.

Замечание. Если непрерывная случайная величинаZявляется функцией непрерывной случайной величины X. Z = ф(Х), то ее математическое ожидание определяется формулой

Свойства математического ожидания определяются рядом теорем.

Если случайная величинах является постоянной, т.е. принимает только одно значение х, = с, то ее математическое ожидание равно этому значению:

Постоянную величину можно рассматривать только как дискретную, поэтому подставляя в (3.6) х- = с, получим

Постоянный множитель можно выносить за знак математического ожидания:

Если X — дискретная случайная величина, то с ? X тоже случайная величина, которая принимает значения сх. с вероятностьюр_р тогда

Если X — непрерывная случайная величина, то с учетом (3.9)

Определение 3.9. Суммой двух независимых случайных величин Хи Yназывается случайная величинаХч- Y, которая принимает все значения видах,+у. (/’ = 1,2,л; / = 1, 2, . т) с вероятностями p_jj = р₍.я., где p_t вероятность появления события X = х. a q_j вероятность появления события Y = у.

Математическое ожидание алгебраической суммы случайных величин равно алгебраической сумме их математических ожиданий

Доказательство По определению

Разобьем двойную сумму на две части

В первом выражении произведениер_<х_<, а во второму не участвует в суммировании по j, учитывая это, а также то, что

Математическое ожидание отклонения случайной величины от ее математического ожидания равно нулю. Действительно, учитывая свойства математического ожидания (см. теоремы 3.1 и 3.3) можно записать:

Определение 3.10. Произведением двух независимых случайных величин X и Y называется случайная величинах — К, которая принимает все значения видах,у. (/ = 1,2. л;/ = 1,2. т) с вероятностями р.. = р₍.о., где р_; вероятность появления события X = х_г а я. вероятность появления события Y=у..

Отметим, что определение 3.10 относится только к независимым случайным величинам поскольку для зависимых случайных величин равенство _Pjj = /хс/, неприменимо, так как одна из вероятностей в этом случае должна быть условной (см. теорему 2.2).

Математическое ожидание двух независимых случайных величин равно произведению их математических ожиданий:

Учитывая то, что р_<.г. не участвуют в суммировании по j, a q.y. не участвуют в суммировании по г, проведем преобразования

Замечание. Все изложенные выше свойства (см. теоремы 3.1—3.4), которые были доказаны для дискретных величин, справедливы также и для непрерывных случайных величин.

Пример 3.3. Пусть X и У две независимые случайные величины с математическими ожиданиями М_х = -1, M_Y = 17. Найти математическое ожидание случайной величины 2Х— ЗУ.

Следующими двумя важными характеристиками случайной величины являются дисперсия и среднее квадратическое отклонение, которые относятся к характеристикам рассеивания.

‘ Определение 3.11. Дисперсией случайной величиныXназывается математическое ожидание квадрата отклонения этой величины от ее математического ожидания:

С помощью (3.6) и (3.8) и используя (3.10) можно записать выражения для дисперсий дискретной и непрерывной случайных величин через их значения х_< и .г соответственно:

? для дискретной случайной величины

? для непрерывной случайной величины

cjp Определение 3.12. Средним квадратическим отклонением случайной величины называется квадратный корень из ее дисперсии:

Отметим, что математическое ожидание и дисперсия являются двумя независимыми характеристиками случайной величины, зная одну из них нельзя определить другую. В то же время дисперсия и среднее квадратическое отклонение взаимозависимы. Введение двух зависимых характеристик рассеивания связано со следующим обстоятельством.

Из определения следует, что дисперсия характеризует среднее значение квадрата отклонения случайной величины от ее математического ожидания, т.е. от среднего значения. Возведение в квадрат отклонения позволяет исключить влияние его знака при усреднении, но при этом возникает различие в единицах измерения случайной величины и ее дисперсии. Именно поэтому вводится еще одна характеристика случайной величины — среднее квадратическое отклонение, которая имеет ту же размерность, что и сама случайная величина. Следующие четыре теоремы определяют свойства дисперсии.

Дисперсия постоянной величины равна нулю:

Рассматривая постоянную величину, как величину, принимающую одно значение с вероятностью единица, запишем

Постоянный множитель можно выносить за знак дисперсии, возводя его при этом в квадрат:

Заменяя в (3.11) х на сх и вынося константу с за знак суммы, получим для дискретной случайной величины

В случае непрерывной случайной величины используя (3.9) и (3.12) после преобразований получим

Дисперсия случайной величины равна разности между математическим ожиданием квадрата этой величины и квадратом ее математического ожидания:

Возведя в квадрат выражение в скобках в (3.10) и используя свойства математического ожидания, преобразуем выражение для дисперсии:

Дисперсия алгебраической суммы или разности независимых случайных величин равна сумме их дисперсий:

Преобразуем формулу для дисперсии суммы двух случайных величин:

Пример 3.4. Найти дисперсию случайной величины, заданную в примере 3.2.

Решение. Воспользуемся формулой (3.13). Значение М(Х) = 3,2 было найдено при решении примера 3.2. Найдем М(Х 2 ):

Формулы для вычисления дисперсии дискретной случайной величины с учетом (3.6), (3.7) можно представить в виде

Для непрерывной случайной величины аналогичные формулы вычисления дисперсии имеют вид

Пример 3.5. Случайная величинаXзадана плотностью распределения /(.г) = 2.г в интервале (0; 1), вне этого интервала/(.г) = 0. Найти математическое ожидание и дисперсию.

Решение. Применяя формулы (3.8) и (3.13), получим