Способы кодирования целых чисел

И ДЕЙСТВИЯ НАД НИМИ

КОДИРОВАНИЕ ЧИСЕЛ В КОМПЬЮТЕРЕ

Способы кодирования и допустимые над ними действия различны для следующих числовых множеств:

· целые положительные числа (целые числа без знака);

· целые числа со знаком;

· вещественные нормализованные числа.

Для записи числа в устройствах компьютера выделяется фиксированное количество двоичных разрядов.

Память компьютера имеет байтовую структуру, однако, размер одной адресуемой ячейки обычно составляет несколько байт.

Например, ячейка памяти объединяет 2 байта (16 двоичных разрядов) — такая комбинация связанных соседних ячеек, обрабатываемая совместно, называется машинным словом.

Для представления числа в регистре арифметико-логического устройства процессора, где формируется результат операции, имеется еще один дополнительный одноразрядный регистр, который называется регистром переноса и который можно рассматривать в качестве продолжения (т.е. 17-го бита) регистра результата.

Назначение этого бита выяснится чуть позже.

Конечный размер разрядной сетки порождает понятие "наибольшее целое число", которого в обычном (немашинном) представлении чисел просто не существует.

Если количество разрядов k и основание системы счисления p=2, то (Z₂)_max = 2 k — 1 .

В частности, при k=16 (Z₂)_max = 2 16 — 1 = 111 1111 1111 1111₂ =65535₁₀.

Таким образом, целого числа, например 65636 и более в компьютере просто не может существовать и, следовательно, появление в ходе вычислений чисел, превышающих (Z₂)_max, должно интерпретироваться как ошибка.

Минимальным целым числом в беззнаковом представлении является (Z₂)_min = 000 0000 0000 0000₂ = 0₁₀.

В языке программирования PASCAL целые числа без знака, для записи которых отводится 2 байта, определены как тип Word.

Тип числа устанавливает способ кодирования этого числа, то есть количество отводимых для записи ячеек памяти (т.е. разрядность числа), а также перечень допустимых операций при обработке.

Выход за границу 65535 возможен только путем увеличения количества разрядов для записи числа, но это порождает новый тип со своим Z_max; например, тип Longint ("целое число со знаком") с максимальным значением 2147483647₁₀, числа которого занимают 4 байта.

С беззнаковыми числами выполняются арифметические операции, не меняющие типа числа; к которым относятся сложение и умножение.

Сложение

Сложение производится согласно таблице сложения, которая для двоичных чисел имеет вид:

В последнем случае в том разряде, где находились слагаемые, оказывается 0, а 1 переносится в старший разряд и называется битом переноса..

Пример 1. Найти сумму 1594₁₀ + 17563₁₀ при беззнаковой двоичной кодировке и 16-битном машинном слове.

После перевода слагаемых в двоичную систему счисления и выполнения сложения получим (для удобства восприятия 16-ти разрядное число разобьем на группы по четыре разряда):

0010 0110 1001 0100

0011 0000 0011 1001

0101 0110 1100 1101

Пример 2. Найти сумму 65534₁₀ + 3₁₀

1111 1111 1111 1110 —Переносы

0000 0000 0000 0011

1 0000 0000 0000 0001

В последнем примере в результате сложения получилось число, превышающее максимально возможное, то есть результат ошибочен, о чем свидетельствует появление 1 в регистре переполнения.

Возникновение такой ситуации в ходе выполнения программы, написанной на языке, где предусмотрено строгое описание типа переменных, приводит к прекращению работы и выводу сообщения об ошибке.

В программах, предназначенных для обработки числовой информации (например, Excel, MathCAD или Calc), при переполнении разрядной сетки производится автоматическое преобразование целого числа в вещественный тип.

Таким образом, регистр переполнения в данном случае служит индикатором корректности процесса вычислений.

Умножение

Умножение производится согласно таблице умножения, которая для двоичных чисел имеет следующий вид:

0 · 0 = 0
0 · 1 = 0
1 · 0 = 0
1 · 1 = 1

Пример 1. Найти произведение 13₁₀ × 5₁₀ . После перевода сомножителей в двоичную систему счисления получим

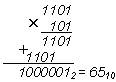
Таким образом, умножение двоичных чисел сводится к операциям сдвига на один двоичный разряд влево и повторения первого сомножителя в тех разрядах, где второй сомножитель содержит 1, и сдвига без повторения в разрядах с 0.

Сдвиг всегда чередуется со сложением из-за ограниченности числа регистров, которые имеются в процессоре для размещения операндов. Другими словами, реализации отдельной операции умножения в процессоре не требуется.

Как и в операции сложения, при умножении чисел с ограниченной разрядной сеткой может возникнуть переполнение. Решается проблема рассмотренными выше способами.

Не нашли то, что искали? Воспользуйтесь поиском:

Лучшие изречения: Увлечёшься девушкой-вырастут хвосты, займёшься учебой-вырастут рога 9987 — | 7776 — или читать все.

91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.

Отключите adBlock!
и обновите страницу (F5)
очень нужно

Десятичное и двоичное представление чисел

Для работы с числовой информацией мы пользуемся системой счисления, содержащей десять цифр: от $0$ до $9$. Эта система называется десятичной.

Кроме цифр, в десятичной системе большое значение имеют разряды. Подсчитывая количество чего-нибудь и дойдя до самой большой из доступных нам цифр (до $9$), мы вводим второй разряд и дальше каждое последующее число формируем из двух цифр. Дойдя до $99$, мы вынуждены вводить третий разряд. В пределах трех разрядов мы можем досчитать уже до $999$ и т.д.

Таким образом, используя всего десять цифр и вводя дополнительные разряды, мы можем записывать и проводить математические операции с любыми, даже самыми большими числами.

Компьютер ведет подсчет аналогичным образом, но имеет в своем распоряжении всего две цифры — логический ноль (отсутствие у бита какого-то свойства) и логическую единицу (наличие у бита этого свойства).

Система счисления, использующая только две цифры, называется двоичной. При подсчете в двоичной системе добавлять каждый следующий разряд приходится гораздо чаще, чем в десятичной.

Попробуй обратиться за помощью к преподавателям

Вот таблица первых десяти чисел в каждой из этих систем счисления:

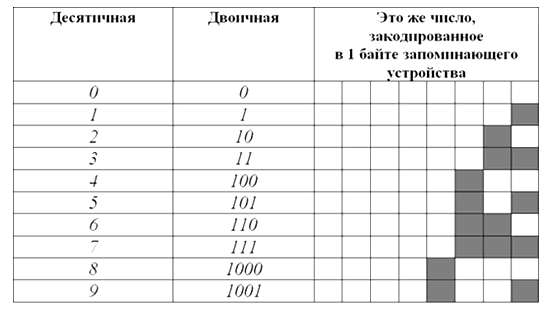
Как видите, в десятичной системе счисления для отображения любой из первых десяти цифр достаточно $1$ разряда. В двоичной системе для тех же целей потребуется уже $4$ разряда.

Соответственно, для кодирования этой же информации в виде двоичного кода нужен носитель емкостью как минимум $4$ бита ($0,5$ байта). Человеческий мозг, привыкший к десятичной системе счисления, плохо воспринимает систему двоичную. Хотя обе они построены на одинаковых принципах и отличаются лишь количеством используемых цифр. В двоичной системе точно так же можно осуществлять любые арифметические операции с любыми числами. Главный ее минус — необходимость иметь дело с большим количеством разрядов.

Задай вопрос специалистам и получи
ответ уже через 15 минут!

Так, самое большое десятичное число, которое можно отобразить в 8 разрядах двоичной системы — $255$, в $16$ разрядах – $65535$, в $24$ разрядах – $16777215$.

Алгоритмы кодирования чисел в двоичной системе счисления

Компьютер, кодируя числа в двоичный код, основывается на двоичной системе счисления. Но, в зависимости от особенностей чисел, может использовать разные алгоритмы:

Небольшие целые числа без знака.

Для сохранения каждого такого числа на запоминающем устройстве, как правило, выделяется $1$ байт ($8$ битов). Запись осуществляется в полной аналогии с двоичной системой счисления.

Целые десятичные числа без знака, сохраненные на носителе в двоичном коде, будут выглядеть примерно так:

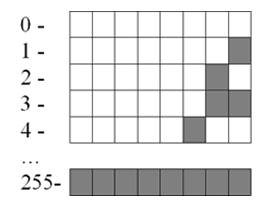
Большие целые числа и числа со знаком.

Для записи каждого такого числа на запоминающем устройстве, как правило, отводится $2$-байтний блок ($16$ битов).

Старший бит блока (тот, что крайний слева) отводится под запись знака числа и в кодировании самого числа не участвует. Если число со знаком "плюс", этот бит остается пустым, если со знаком "минус" – в него записывается логическая единица. Число же кодируется в оставшихся 15 битах. Например, алгоритм кодирования числа $+2676$ будет следующим:

• Перевести число $2676$ из десятичной системы счисления в двоичную. В итоге получится $101001110100$;
• Записать полученное двоичное число в первые $15$ бит $16$-битного блока (начиная с правого края). Последний, $16$-й бит, должен остаться пустым, поскольку кодируемое число имеет знак $+$.

В итоге $+2676$ в двоичном коде на запоминающем устройстве будет выглядеть так:

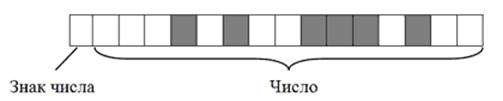
Примечательно, что в двоичном коде присвоение числу отрицательного значения предусматривает не только изменение старшего бита. Осуществляется также инвертирование всех остальных его битов.

Чтобы было понятно, рассмотрим алгоритм кодирования числа $-2676$:

1. Перевести число $2676$ из десятичной системы счисления в двоичную. Получим все тоже двоичное число $101001110100$;
2. Записать полученное двоичное число в первые $15$ бит $16$-битного блока. Затем инвертировать, то есть, изменить на противоположное, значение каждого из $15$ битов;
3. Записать в $16$-й бит логическую единицу, поскольку кодируемое число имеет отрицательное значение.

В итоге $-2676$ на запоминающем устройстве в двоичном коде будет иметь следующий вид:

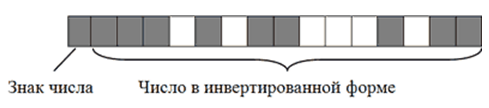
Запись отрицательных чисел в инвертированной форме позволяет заменить все операции вычитания, в которых они участвуют, операциями сложения. Это необходимо для нормальной работы компьютерного процессора.

Максимальным десятичным числом, которое можно закодировать в $15$ битах запоминающего устройства, является $32767$. Иногда для записи чисел по этому алгоритму выделяются $4$-байтные блоки. В таком случае для кодирования каждого числа будет использоваться $31$ бит плюс $1$ бит для кодирования знака числа. Тогда максимальным десятичным числом, сохраняемым в каждую ячейку, будет $2147483647$ (со знаком плюс или минус).

Дробные числа со знаком.

Дробные числа на запоминающем устройстве в двоичном коде кодируются в виде так называемых чисел с плавающей запятой (точкой). Алгоритм их кодирования сложнее, чем рассмотренные выше. Тем не менее, попытаемся разобраться.

Для записи каждого числа с плавающей запятой компьютер чаще всего выделяет $4$-байтную ячейку ($32$ бита):

• в старшем бите этой ячейки (тот, что крайний слева) записывается знак числа. Если число отрицательное, в этот бит записывается логическая единица, если оно со знаком "плюс" – бит остается пустым.
• во втором слева бите аналогичным образом записывается знак порядка (что такое порядок поймете позже);
• в следующих за ним $7$ битах записывается значение порядка.
• в оставшихся $23$ битах записывается так называемая мантисса числа.

Чтобы стало понятно, что такое порядок, мантисса и зачем они нужны, переведем в двоичный код десятичное число $6,25$.

Порядок кодирования будет примерно следующим:

1. Перевести десятичное число в двоичное (десятичное $6,25$ равно двоичному $110,01$);
2. Определить мантиссу числа. Для этого в числе необходимо передвинуть запятую в нужном направлении, чтобы слева от нее не осталось ни одной единицы. В нашем случае запятую придется передвинуть на три знака влево. В итоге, получим мантиссу, $11001$;
3. Определить значение и знак порядка. Значение порядка – это количество символов, на которое была сдвинута запятая для получения мантиссы. В нашем случае оно равно $3$ (или $11$ в двоичной форме);

Знак порядка – это направление, в котором пришлось двигать запятую: влево – "плюс", вправо – "минус". В нашем примере запятая двигалась влево, поэтому знак порядка – "плюс".

Таким образом, порядок двоичного числа $110,01$ будет равен $+11$, а его мантисса, $11001$. В результате в двоичном коде на запоминающем устройстве это число будет записано следующим образом

Обратите внимание, что мантисса в двоичном коде записывается, начиная с первого после запятой знака, а сама запятая упускается. Числа с плавающей запятой, кодируемые в $32$ битах, называю числами одинарной точности. Когда для записи числа $32$-битной ячейки недостаточно, компьютер может использовать ячейку из $64$ битов. Число с плавающей запятой, закодированное в такой ячейке, называется числом двойной точности.

Так и не нашли ответ
на свой вопрос?

Просто напиши с чем тебе
нужна помощь

Особенность представления чисел в памяти компьютера – ячейки имеют ограниченный размер, а это вынуждает использовать при записи чисел и действиях с ними конечное число разрядов. В зависимости от типа числа определяется способ кодирования, количество отводимых под число ячеек памяти (разрядность числа) и перечень допустимых операций при обработке. Способы кодирования чисел и допустимые над ними действия различны для следующих числовых множеств:

целые положительные числа (без знака)

целые со знаком

вещественные нормализованные числа. (иррац (бесконечные непериодические дроби, Пи, корень из двух..) и рацион (m/n или бесконечные периодические дроби))

Целые числа без знака.

Память в компьютере имеет байтовую структуру. Целые без знака обычно занимают один, два или более байт. В однобайтовом формате они могут принимать значения в диапазоне от 0 до 255, в двухбайтовом от 0 до 65535. Здесь попытка представить в байтовом формате число 258 будет интерпретироваться как ошибка.

Представляются целые числа без знака в своем двоичном виде.

в байтовом формате:

Над целыми числами определены операции сложения (по правилам двоичного сложения) и умножения (по правилам двоичного умножения). Определены именно эти операции, так как они не меняют тип результата. Вычитание и деление не определены.

Целые числа со знаком

Используются три формы записи целых чисел со знаком: прямой код, обратный код, дополнительный код.

При кодировании прямым n-разрядным двоичным кодом один разряд (как правило самый старший) отводится для знака числа. Остальные n-1 разрядов – для значащих цифр. Значение знакового разряда равно 0 для положительных чисел, 1 – для отрицательных.

Пример: 1 = 0000 0001, -1 = 1000 0001

Он получается инвертированием всех цифр двоичного кода абсолютной величины числа.

код модуля: 00000001

обратный код: 11111110

Отрицательные числа в компьютерах представляются в ДОПОЛНИТЕЛЬНОМ КОДЕ . Для получения дополнительного кода двоичного числа необходимо инвертировать это число (заменить все 0 на 1, а 1 на 0) , т.е получить обратный код числа, а затем прибавить в младшем разряде 1.

Например: Используется 6 разрядное представление двоичных чисел. 7 = 000111; -7 = 111001 – это дополнительный код.

Дополнительный код получен так:

1) инверсия 000111 равна 111000:

111001 – это представление числа -7 в дополнительном коде.

При таком представлении чисел вычитание двух чисел А – В выполняется как сложение А + (-В).

Например: 001100 = 12

111001 = -7 в дополнительном коде

единица переноса в старший разряд при выполнении операции

Таким образом, отпадает необходимость в отдельном устройстве для операции вычитания.

Пример: Для числа -1101:

Замечание: для положительных чисел представление числа в прямом, обратном и дополнительном кодах совпадают. Т. образом – положительные числа всегда изображаются одинаково – двоичными кодами с цифрой 0 в знаковом разряде.

над целыми без знака определены сложение, вычитание (сводится к сложению с дополнительным кодом), умножение, целочисленное деление и нахождение остатака от деления.

Сдвиг числа на один разряд влево увеличивает число в 2 раза; сдвиг на один разряд вправо – уменьшает его в 2 раза:

В компьютерах числа представляются в двоичной форме с определенным количеством разрядов. Обычно разрядность компьютеров равна одному из следующих значений: 8, 16, 32, 64.

Ограниченная разрядность приводит к ограничению диапазона используемых чисел. Если разрядность компьютера равна n, то количество различных чисел, которые можно представить с помощью n-разрядных двоичных последовательностей будет равна

Например, если разрядность компьютера равна 16, то количество различных двоичных последовательностей будет равно

2 16 = 2 6+10 = 64 * 1024 = 65536.

Для кодирования чисел в компьютере существуют два основных формата: для кодирования целых чисел и для задания действительных чисел — представление числа в формате с плавающей точкой. Рассмотрим кодирование целых чисел.

Для каждого числа в памяти компьютера отводится К ячеек (8, 18, 24, 32). В К-разрядной ячейке может храниться 2 k различных значений целых чисел .

В 8 разрядной ячейке может храниться число в диапазоне от 0 до 255 или от ‑128 до 127 (всего 256=2 8 чисел).

Для того, чтобы получить целое положительного числа N, хранящееся в к‑разрядной ячейке памяти компьютера, необходимо:

1) перевести число N в двоичную систему счисления;

2) полученный результат дополнить слева незначащими нулями до К разрядов.

Для записи целого отрицательного числа (-N) необходимо:

1) получить внутреннее представление положительного числа N; или прямой код числа

2) обратный код этого числа заменой 0 на 1 и 1 на 0;

3) полученному числу прибавить 1 (дополнительный код числа).

Запишем отрицательное число –126 в 8 битном формате.

Прямой код числа 126=0111 1110,

обратный код числа 1000 0001, после прибавления 1 получим дополнительный код -126=1000 0010

Запишем отрицательное число – 7в 8 битном формате.

Прямой код числа 7=0000 0111,

обратный код числа 1111 1000, после прибавления 1 получим дополнительный код -7=1111 1001

Формат с плавающей точкой

использует представление вещественного числа R в виде произведения мантиссы m на основание системы счисления n в некоторой целой степени p (основание системы счисления), которую называют порядком: R = m * n p. Представление числа в форме с плавающей точкой неоднозначно.

Пример 4. Справедливы следующие равенства:

52.345 = 0.0052345 x 10 4 = 5234.5 x 10 -2 = 0.52345 x 10 2

В ЭВМ используют нормализованное представление числа в форме с плавающей точкой. Мантисса в таком представлении должна удовлетворять условию: 0.1 p Выбор читателей