Схема частичного выбора метода гаусса

1. На первом шаге прямого хода метода Гаусса выбирается максимальный по модулю элемент в первом столбце. Этот элемент является ведущим. Если он равен нулю, то detA = 0. Если ведущий элемент не является элементом , то перестановкой строк помещаем его в . При этом соответственно переставляются элементы вектора b. Затем применяются формулы метода Гаусса.

2. На -м шаге прямого хода метода Гаусса непреобразованный столбец – это часть столбца i, начиная с элемента , то есть . Находим максимальный по модулю элемент в непреобразованном столбце. Этот элемент является ведущим. Если он равен нулю, то detA = 0. Если ведущий элемент не является элементом , то перестановкой строк помещаем его в . При этом соответственно переставляются элементы вектора b. Затем применяются формулы метода Гаусса.

3. После (n-1)-го шага получаем верхнюю треугольную матрицу U и преобразованный вектор правой части. Выполняем обратную подстановку.

Метод Гаусса с частичным выбором ведущего элемента в отсутствие ошибок округления для невырожденных матриц позволяет получить точное решение, а для вырожденных матриц – сообщение о том, что матрица вырождена.

Решить систему линейных уравнений методом Гаусса с частичным выбором ведущего элемента.

Рассмотрим ту же систему линейных уравнений, что и в предыдущих примерах.

Прямой ход метода Гаусса

Прежде всего, выбираем максимальный по модулю элемент в первом непреобразованном столбце:

, , следовательно, ведущим элементом является 10.

Ведущим элементом является элемент , поэтому перестановка строк не нужна. Умножим первое уравнение на 0.3 и прибавим ко второму. Умножим первое уравнение на -0.5 и прибавим к третьему. Получим:

Рассмотрим следующий непреобразованный столбец:

, , следовательно, ведущим элементом является 2.5, а не -0.1, как в методе Гаусса без выбора ведущего элемента. Но ведущий элемент не является элементом ( при ) , поэтому необходимо переставить строки матрицы А, чтобы элемент 2.5 стал элементом .

Умножим второе уравнение на 0.4 и прибавим к третьему. Получим:

Мы получили систему линейных уравнений с верхней треугольной матрицей.

Ведущими элементами являются числа: 10, 2.5, 6.2, все они по модулю больше 1, следовательно, алгоритм является вычислительно устойчивым.

В методе Гаусса с частичным выбором ведущего элемента, в отличие от метода Гаусса без выбора ведущего элемента, в случае необходимости меняются местами уравнения системы линейных уравнений. За счет этого не возникает проблем, если у невырожденной матрицы какой-либо из главных миноров равен нулю.

Рассмотрим метод Гаусса с частичным выбором ведущего элемента с точки зрения операций над матрицами.

Произвольная невырожденная матрица перестановкой строк (столбцов) может быть приведена к матрице с главными минорами, отличными от нуля ( , где P – матрица перестановок).

Матрица Р получается из единичной матрицы перестановкой строк (столбцов).

Сложность метода Гаусса с частичным выбором ведущего элемента

Число арифметических действий, необходимых для его реализации: , где n – число уравнений. Оценим сложность по памяти: требуется память для хранения n 2 элементов матрицы, вектора b (n элементов) и вектора x (n элементов), в результате, .

Метод Гаусса с частичным выбором ведущего элемента является устойчивым, если все ведущие элементы по модулю больше единицы.

Следует отметить, что метод Гаусса с частичным выбором ведущего элемента – это основной алгоритм вычислительной математики линейной алгебры.

Метод Гаусса с полным выбором ведущего элемента отличается от метода Гаусса с частичным выбором ведущего элемента тем, что на каждом шаге прямого хода ведущий элемент ищется в непреобразованной части матрицы. Непреобразованная часть матрицы – это квадратная матрица размерности n-i+1, получаемая вычеркиванием первых i – 1 строк и первых i – 1 столбцов. В методе Гаусса с полным выбором ведущего элемента возможна не только перестановка строк матрицы и соответствующих элементов правой части, но и перестановка столбцов матрицы и, соответственно, изменение порядка следования неизвестных.

Срочно?
Закажи у профессионала, через форму заявки
8 (800) 100-77-13 с 7.00 до 22.00

На k-ом шаге прямого хода в качестве ведущего элемента выбирают максимальный по модулю коэффициент 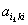при неизвестной 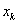в уравнениях с номерами i = k+1, . , m.Затем уравнение, соответствующее выбранному коэффициенту с номером , меняют местами с к-ым уравнением системы для того, чтобы главный элемент занял место коэффициента 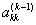. После этой перестановки исключение проводят как в схеме единственного деления. В этом случае все масштабирующие множители по модулю меньше единицы и схема обладает вычислительной устойчивостью.

ПРИМЕР 1.Решение системы методом Гаусса с выбором главного элемента по столбцу.

A= 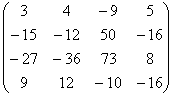, b= .

Прямой ход. 1 шаг. Максимальный по модулю элемент 1-го столбца 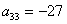. Переставим 1-ое и 3 — е уравнения местами:

A= , b= .

Вычислим масштабирующие множители 1 шага:

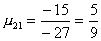
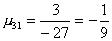
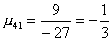
и выполним преобразование матрицы и вектора:

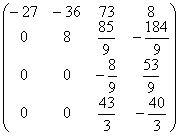A1= b1= .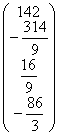

2 шаг. Вычислим масштабирующие множители 2 шага:

.

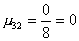
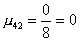Второй шаг не изменяет матриц: A2=A1, b2= b1.

3 шаг. Максимальный по модулю элемент 3 столбца . Переставим 3 и 4 уравнения местами.

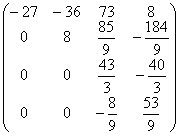A2= b2= .

Вычислим масштабирующие множители 3 шага:

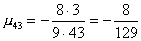
и выполним преобразование матрицы и вектора:

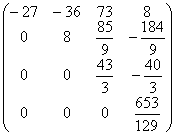A3= b3= .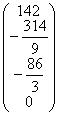

Обратный ход. Из последнего уравнения находим: 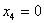. Из третьего

уравнения системы находим 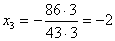. Из второго уравнения находим

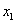. Неизвестное находим из первого уравнения:

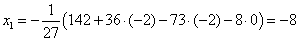
Ответ: .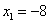

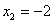
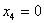% Решить систему Ax=b методом Гаусса

% Введём правую часть

b = [-14; 44; 142; -76];

% Решим систему средствами MATLAB

x =	-8.0000
-2.0000
-2.0000
-0.0000

Не нашли то, что искали? Воспользуйтесь поиском:

Лучшие изречения: При сдаче лабораторной работы, студент делает вид, что все знает; преподаватель делает вид, что верит ему. 9526 — | 7348 — или читать все.

91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.

Отключите adBlock!
и обновите страницу (F5)
очень нужно

Одним из самых распространенных методов решения систем линейных уравнений является метод Гаусса. Этот метод (который также называют методом последовательного исключения неизвестных) известен в различных вариантах уже более 2000 лет.

Вычисления с помощью метода Гаусса заключаются в последовательном исключении неизвестных из системы для преобразования ее к эквивалентной системе с верхней треугольной матрицей. Вычисления значений неизвестных производят на этапе обратного хода.

Схема единственного деления

Рассмотрим сначала простейший вариант метода Гаусса, называемый схемой единственного деления.

Прямой ход состоит из n 1 шагов исключения.

1-й шаг. Целью этого шага является исключение неизвестного x₁ из уравнений с номерами i = 2, 3, …, n. Предположим, что коэффициент a₁₁ 0. Будем называть его главным элементом 1-го шага.

называемые множителями 1-го шага. Вычтем последовательно из второго, третьего, …, n-го уравнений системы первое уравнение, умноженное соответственно на q₂₁, q₃₁, …, q_n1. Это позволит обратить в нуль коэффициенты при x₁ во всех уравнениях, кроме первого. В результате получим эквивалентную систему

2-й шаг. Целью этого шага является ислючение неизвестного x₂ из уравнений с номерами i = 3, 4, …, n. Пусть a₂₂ (1) ? 0, где a₂₂ (1) — коэффициент, называемый главным (или ведущим) элементом 2-го шага. Вычислим множители 2-го шага

и вычтем последовательно из третьего, четвертого, …, n-го уравнения системы второе уравнение, умноженное соответственно на q₃₂, q₄₂, …, q_m2. В результате получим систему

Здесь коэффициенты a_ij (2) и b_ij (2) вычисляются по формулам

Аналогично проводятся остальные шаги. Опишем очередной k-й шаг.

k-й шаг. В предположении, что главный (ведущий) элемент k-го шага a_kk (k — 1) отличен от нуля, вычислим множители k-го шага

и вычтем последовательно из (k + 1)-го, …, n-го уравнений полученной на предыдущем шаге системы k-e уравнение, умноженное соответственно на q_k+1,k, q_k+2,k, …, q_nk.

После (n — 1)-го шага исключения получим систему уравнений

матрица A (n-1) которой является верхней треугольной. На этом вычисления прямого хода заканчиваются.

Обратный ход. Из последнего уравнения системы находим xn. Подставляя найденное значение x_n в предпоследнее уравнение, получим x_n—₁. Осуществляя обратную подстановку, далее последовательно находим x_n—₁, x_n—₂, …, x₁. Вычисления неизвестных здесь проводятся по формулам

Необходимость выбора главных элементов. Заметим, что вычисление множителей, а также обратная подстановка требуют деления на главные элементы a_kk (k — 1) . Поэтому если один из главных элементов оказывыется равным нулю, то схема единственного деления не может быть реализована. Здравый смысл подсказывает, что и в ситуации, когда все главные элементы отличны от нуля, но среди них есть близкие к нулю, возможен неконтролируемый рост погрешности.