Примеры затухающих колебаний из жизни

Математический маятник (рис. 5)

Физический маятник (рис. 4)

Пружинный маятник (рис. 3)

Одномерный классический гармонический осциллятор

Общие сведения о колебаниях.

Колебаниями называются процессы, отличающиеся той или иной степенью повторяемости. В зависимости от физической природы повторяющегося процесса различают колебания: механические, электромагнитные, электромеханические и т.д. Рассмотрим механические колебания.

В зависимости от характера воздействия на колеблющуюся систему различают свободные (или собственные) колебания, вынужденные колебания, автоколебания и параметрические колебания.

Силу, под действием которой происходит колебательный процесс, называют возвращающей силой, так как она стремится вернуть тело или материальную точку в положение равновесия.

Свободные колебания совершаются системой, выведенной из положения равновесия.

Собственныминазываются свободные колебания без учёта сил сопротивления (без затухания).

Вынужденныминазываются такие колебания, в процессе которых колеблющаяся система подвергается воздействию внешней периодически изменяющейся силы. Примером служат колебания моста, возникающие при прохождении по нему людей, шагающих в ногу.

Автоколебания, как и вынужденные колебания, сопровождаются воздействием на колеблющуюся систему внешних сил, однако моменты времени, когда осуществляются эти воздействия, задаются самой колеблющейся системой – система сама управляет внешним воздействием. Примером автоколебательной системы являются часы, в которых маятник получает толчки за счёт энергии поднятой гири или закрученной пружины, причем эти толчки происходят в моменты прохождения маятника через среднее положение.

При параметрических колебаниях за счёт внешнего воздействия происходит периодическое изменение какого-либо параметра системы, например, длины нити, к которой подвешен шарик, совершающий колебания.

Простейшими являются гармонические колебания, при которых колеблющаяся величина (например, отклонение маятника) изменяется со временем по закону синуса или косинуса. Этот вид колебаний особенно важен по следующим причинам: во-первых, колебания в природе и в технике часто имеют характер, очень близкий к гармоническому, во-вторых, периодические процессы иной формы (с другой зависимостью от времени) могут быть представлены как наложение нескольких гармонических колебаний. Гармонические колебания удобно представить в виде круговой диаграммы (рис.1). Пусть точка движется по окружности радиусом 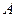. Её положение задаётся радиус-вектором . Положение равновесия задаётся точкой 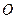. Радиус-вектор равномерно вращается с угловой скоростью 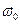. Проекции радиус-вектора на оси или 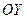задаются математическими выражениями (уравнениями) гармонических колебаний:

(1)

(2)

Мы будем использовать уравнение гармонических колебаний в виде (1). Координата 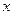задаёт значение колеблющейся величины. Величина 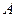– амплитуда колебаний, т.е. максимальное отклонение колеблющейся точки от положения равновесия. Величина , равная числу колебаний за время секунды, называется циклической частотой. Аргумент косинуса 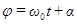, характеризующий значение колеблющейся величины в момент времени , называется фазойколебаний. Фаза колебаний , соответствующая начальному моменту времени, называется начальной фазой колебаний. Время одного полного колебания 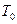называется периодом колебаний. Число колебаний 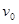за время, равное одной секунде, называется частотойколебаний.

.

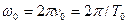Скорость колеблющейся точки находится дифференцированием выражения (1) по времени:

(3)

Дифференцируя вторично, получаем ускорение:

. (4)

.

На рис. 2 представлены зависимости . Скорость опережает смещение на 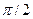, ускорение находится в противофазе по отношению к смещению.

Каждое конкретное колебание характеризуется определенным значением амплитуды 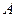и начальной фазы . Определим их значения из начальных условий . В этом случае 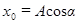, . Отсюда следует, что

, .

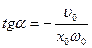Выведем дифференциальное уравнение гармонических колебаний. Из выражения (4) следует, что

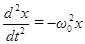или . (5)

Уравнение (5) является дифференциальным уравнением гармонических колебаний. Это уравнение является общим уравнением, описывающим гармонические колебания. Его решением являются функции (1) или (2). Следовательно, можно сказать, что гармоническиминазываются колебания, совершаемые по закону синуса или косинуса.

Колебательные системы, описываемые уравнением (5) называются одномерным классическим гармоническим осциллятором.Модель одномерного классического гармонического осциллятора оказывается справедливой не только для механических, но и других видов собственных незатухающих колебаний. В различных разделах физики используется единый математический язык описания гармонических колебаний.

Рассмотрим конкретные примеры гармонических осцилляторов в механике.

Применим к движению груза на пружине второй закон Ньютона: , где — сила упругости: ,

. (6)

Сравнивая (5) и (6), получаем:

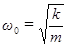(7)

(8)

Мы нашли собственную циклическую частоту (7) и период колебаний (8) груза на пружине.

Физическим маятником называется твердое тело, колеблющееся относительно неподвижной горизонтальной оси (оси подвеса), не проходящей через центр тяжести. При небольших углах отклонения (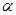-мал) физический маятник совершает гармонические колебания. Сила, возвращающая маятник в положение равновесия, представляет собой составляющую силы тяжести, приложенную в точке :

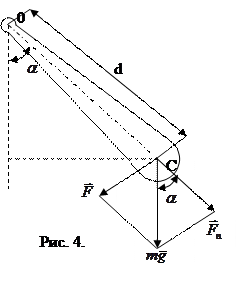
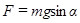
Момент этой силы относительно оси 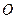равен:

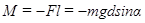, где 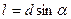— плечо силы 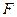относительно оси 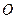, знак минус соответствует тому, что момент стремится вернуть маятник в положение равновесия, аналогично квазиупругой силе.

В соответствии с уравнением динамики вращательного движения

, где 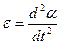— угловое ускорение, 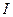— момент инерции маятника относительно оси О. Получаем

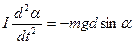. (9)

Ограничившись малыми колебаниями 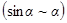, после преобразований получаем уравнение (9) в виде:

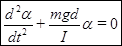(10).

Сравнив выражения (5) и (10) мы видим их математическую аналогию, что позволяет записать выражения для циклической частоты и периода колебаний физического маятника:

(11)

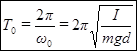, (12)

где 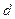-расстояние от центра тяжести до оси вращения.

Если период колебаний не зависит от амплитуды, то такие колебания называются изохронными. Мы видим, что малые колебания физического маятника изохронны. Колебания приближенно изохронны, когда угловая амплитуда колебаний не превышает нескольких градусов. При больших амплитудах изохронность нарушается. На свойстве изохронности колебаний маятника основано его применение в часах.

Математический маятник является частным случаем физического маятника. Математическим маятником называют идеализированную систему, состоящую из невесомой и нерастяжимой нити, к которой подвешена масса, сосредоточенная в одной точке. Примером математического маятника может служить шарик, подвешенный на длинной нити. В случае математического маятника 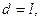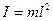,где 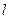-длина математического маятника. Тогда формулы (11) и (12) запишутся в виде:

(13)

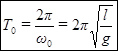(14)

Сравнивая формулы (12) и (14), заключаем, что физический маятник колеблется с периодом математического маятника, длина которого

,

называется приведенной длиной физического маятника.

рассматривать колебание (19) как гармоническое колебание частоты , амплитуда которого изменяется по некоторому закону. Выражением этого закона не может быть множитель, стоящий в скобках, так как он изменяется от 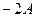до , в то время, как амплитуда по определению – величина положительная. График амплитуды показан на рис 7.б. Аналитическое выражение амплитуды, очевидно, имеет вид:

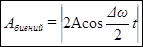. (20)

Функция (20) – периодическая функция с частотой в два раза превышающей частоту выражения, стоящего под знаком модуля, т.е. с частотой . Заменяя в выражении (19) амплитуду через значение (20), получаем уравнение биений:

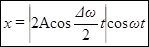(21)

(Затухающие колебания. Дифференциальное уравнение затухающих колебаний и его решение Коэффициент затухания. Время релаксации. Период затухаю­щих колебаний. Декремент затухания. Логарифмический декремент затухания. Добротность колебательной системы. Диссипация энергии.)

|	следующая лекция ==>
|	Гармонический осциллятор при наличии сил сопротивления

Дата добавления: 2013-12-12 ; Просмотров: 1216 ; Нарушение авторских прав? ;

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

В 1:56 поступил вопрос в раздел ЕГЭ (школьный), который вызвал затруднения у обучающегося.

Вопрос вызвавший трудности

Ответ подготовленный экспертами Учись.Ru

Для того чтобы дать полноценный ответ, был привлечен специалист, который хорошо разбирается требуемой тематике "ЕГЭ (школьный)". Ваш вопрос звучал следующим образом: ‘Почему свободные колебания являются затухающими? Приведите примеры затухающих колебаний.’

После проведенного совещания с другими специалистами нашего сервиса, мы склонны полагать, что правильный ответ на заданный вами вопрос будет звучать следующим образом:

НЕСКОЛЬКО СЛОВ ОБ АВТОРЕ ЭТОГО ОТВЕТА:

Работы, которые я готовлю для студентов, преподаватели всегда оценивают на отлично. Я занимаюсь написанием студенческих работ уже более 4-х лет. За это время, мне еще ни разу не возвращали выполненную работу на доработку! Если вы желаете заказать у меня помощь оставьте заявку на этом сайте. Ознакомиться с отзывами моих клиентов можно на этой странице.

Калинина Лили Донатовна — автор студенческих работ, заработанная сумма за прошлый месяц 86 400 рублей. Её работа началась с того, что она просто откликнулась на эту вакансию

ПОМОГАЕМ УЧИТЬСЯ НА ОТЛИЧНО!

Выполняем ученические работы любой сложности на заказ. Гарантируем низкие цены и высокое качество.

Определение и причины затухания колебаний

Причина затухания заключается в том, что во всякой колебательной системе, кроме возвращающей силы, всегда действуют разного рода силы трения, сопротивление воздуха

и т. п., которые тормозят движение. При каждом размахе часть полной колебательной энергии (потенциальной и кинетической) расходуется на работу против сил трения. В конечном итоге на эту работу уходит весь запас энергии, сообщенный колебательной системе первоначально.

Рассматривая свободные гармонические колебания, мы имели дело с идеальными, строго периодическими собственными колебаниями. Описывая при помощи такой модели реальные колебания, мы сознательно допускаем неточность в описании. Однако подобное упрощение является пригодным в силу того, что у многих колебательных систем затухания колебаний, вызванные трением, действительно малы: система успевает совершить много колебаний прежде, чем их амплитуда уменьшится заметным образом.

Графики затухающих колебаний

При наличии затухания собственное колебание (рис.1) перестает быть гармоническим. Более того, затухающее колебание перестает быть периодическим процессом — трение влияет не только на амплитуду колебаний (то есть является причиной затухания), но и на продолжительность размахов. С увеличением трения время, необходимое системе для совершения одного полного колебания, увеличивается. График затухающих колебаний представлен на рис. 2.

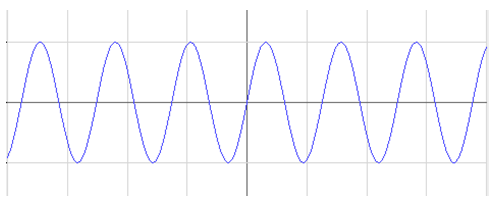
Рис.1. График свободных гармонических колебаний

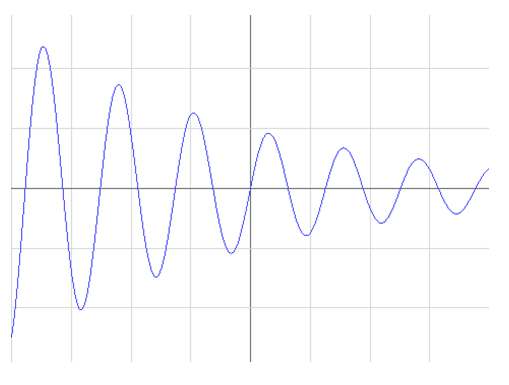
Рис.2. График затухающих колебаний

Характерной чертой колебательных систем является то, что небольшое трение влияет на период колебаний в гораздо меньшей степени, чем на амплитуду. Это обстоятельство сыграло огромную роль в усовершенствовании часов. Первые часы с маятником построил голландский физик и математик Христиан Гюйгенс в 1673 г. Этот год можно считать датой рождения современных часовых механизмов. Ход часов с маятником мало чувствителен к изменениям, обусловленным трением, которые в общем случае зависят от многих факторов, в то время как скорость хода предшествующих безмаятниковых часов очень сильно зависела от трения.

На практике возникает потребность как в уменьшении, так и в увеличении затухания колебаний. К примеру, при конструировании часовых механизмов стремятся уменьшить затухание колебаний балансира часов. Для этого ось балансира снабжают острыми наконечниками, которые упираются в хорошо отполированные конические подпятники, выполненные из твердого камня (агата или рубина). Наоборот, во многих измерительных приборах очень желательно, чтобы подвижная часть устройства устанавливалась в процессе измерений быстро, но совершая большого числа колебаний. Для увеличения затухания в этом случае применяют различные демпферы – устройства, увеличивающие трение и, в общем случае, потерю энергии.