Одним из основных понятий теории вероятностей является оnыт. Под оnытом понимается выполнение комплекса условий, в результате которого происходят или не происходят определенные события (факты).
Простейшие неразложимые результаты опыта называются элементарными событиями (ωi), а вся совокупность элементарных событий называется nространством элементарных событий Ω=<ωi>. С каждым опытом связано свое пространство элементарных событий Ω. Например, игральная кость подбрасывается один раз. Элементарные события: w1 – появление 1, w2 – 2, w3 – 3, w4 – 4, w5 – 5, w6 – 6. Пространство элементарных событий W=1, w2, w3, w4, w5, w6>.
Любое конечное или счетное подмножество Ω, называется событием. Различают три типа событий:
1) достоверные, которые всегда произойдут в результате опыта (Ω);
2) случайные, могут либо произойти в результате опыта, либо нет;
3) невозможные, никогда не произойдут в результате опыта (0 или 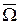 ).
).
События обычно обозначают первыми прописными буквами латинского алфавита: A, В, С.
События A и В несовместны, если в результате одного опыта они не могут происходить одновременно, в противном случае — совместны. Например, при одном подбрасывании монеты не могут одновременно появиться герб и решка.
Элементы последовательности событий A1, A2. An nоnарно несовместны, если любые два из них несовместны. Например, при подбрасывании игральной кости никакие два элементарные исхода (появление цифр 1, 2, 3, 4, 5, 6) не могут произойти одновременно.
Несколько событий равновозможны, если ни одно из них не имеет объективного преимущества перед другими. Например, элементарные исходы при подбрасывании монеты, игральной кости.
События А1, A2. An образуют nолную груnnу, если в результате опыта кроме этих событий ничего не может произойти.
Приведем примеры полных групп событий:
— выигрыш и проигрыш в лотерее для одного лица;
— выпадение «герба» и «цифры» при бросании одной монеты;
— появление числа очков 1, 2, 3, 4, 5, 6 в опыте с игральной костью;
— появление четной или нечетной цифры в том же опыте.
Обычно Ω изображают на плоскости в виде некоторой области, а ωi в виде точек этой области, устанавливая, таким образом, соответствие между событиями и точечными множествами.
Для действий над событиями вводятся операции, совпадающие с операциями над множествами: сумма, произведение, отрицание.
Суммой событий A и В называется такое третье событие A+В (или AÈВ), которое заключается в наступлении хотя бы одного из событий или А, или В (рис. 1.1.1).
Если A и В несовместны, то появление обоих вместе отпадает и сумма сводится к появлению любого из событий, безразлично какого (рис.1.1.1). Можно складывать несколько событий.
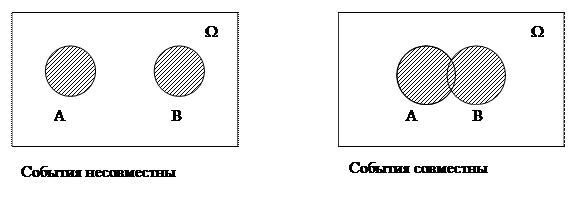
Рис. 1.1.1. Сумма событий
Разберем это на следующих примерах.
Пример 1. Опыт: вынимают наугад одну карту из колоды. События: A – появление червоной масти, В – появление бубновой масти. A и В — несовместные события. Сумма событий:
S = A + B — появление красной масти (безразлично какой).
Пример 2. Дана часть электрической цепи (рис. 1.1.2). События: R1 – обрыв первого сопротивления, R2 – обрыв второго сопротивления. S = R1 + R2 – обрыв цепи между точками C и D. В данном случае R1 и R2 — совместные события, поэтому под их суммой подразумевается обрыв хотя бы одного сопротивления (последовательное соединение), т.е. первого или второго, либо обоих вместе.
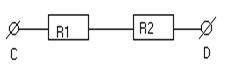
Рис. 1.1.2. Иллюстрация к примеру 2
Пример 3. Опыт: бросают игральную кость. События: A – выпадение цифры 1, В – выпадение цифры 3, С – выпадение цифры 5. A, В, С – несовместные события. S = A + B + C – появление нечетной цифры, т. е. выпадение либо 1, либо 3, либо 5.
Пример 4. Опыт: проводят соревнования по футболу, баскетболу и волейболу. События: A – друзья пошли на футбол, В – друзья пошли на баскетбол, С – друзья пошли на волейбол. A, В, С – несовместные события.
S = A + B + C – друзья пошли на соревнования.
Если в условиях данного опыта несколько событий A1, A2,…, An образуют полную группу, то их сумма является достоверным событием.
Произведением двух событий A и В называется такое третье событие A·В (или A∩В), которое заключается в наступлении событий A и В одновременно. Если события A и В несовместны, то A×В=Æ (рис. 1.1.3).

Рис. 1.1.3. Произведение событий
Пример 5.Опыт: вынимают наугад одну карту из колоды. События: A – появление туза, В – появление бубновой масти.
C = A · В – появление бубнового туза.
Пример 6. Опыт: бросание трех монет.
A1 – выпадение «герба» на первой монете,
В1 – выпадение «решки» на первой монете,
A2 – «герб» на второй монете,
В2 – «решка» на второй монете,
A3 – «герб» на третьей монете,
В3 – «решка» на третьей монете.
Если события несовместны, то их произведение — невозможное событие.
Отрицанием события A называется событие  (не A), заключающееся в ненаступлении события A (
(не A), заключающееся в ненаступлении события A (  Æ,
Æ, 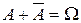 ). Причем, если в результате опыта может произойти событие A, то может произойти и обратное ему событие
). Причем, если в результате опыта может произойти событие A, то может произойти и обратное ему событие  (рис. 1.1.4).
(рис. 1.1.4).
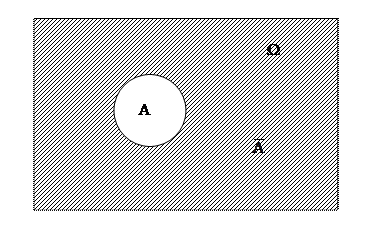
Рис. 1.1.4.  — отрицание события А
— отрицание события А
Пример7. Проводят следующий опыт: один выстрел по мишени. В этом случае событие A – попадание в десятку, противоположное событие`  – непопадание в десятку.
– непопадание в десятку.
Если наступление события A приводит к наступлению события В и наоборот (наступление В влечет наступление A), то события A и В равны (A=В).
Пусть S — множество всех подмножеств Ω, для которого выполняются следующие свойства:
3) если 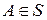 , то
, то 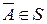 , тогда множество S называется алгеброй событий или s-алгеброй.
, тогда множество S называется алгеброй событий или s-алгеброй.
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Да какие ж вы математики, если запаролиться нормально не можете. 8544 —  | 7399 —
| 7399 —  или читать все.
или читать все.
91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
В этой лекции мы изложим теоретико-множественный подход к основным понятиям теории вероятностей. Пусть проводится некоторый эксперимент со случайным исходом. Результатом эксперимента всегда является один и только один исход из полной группы несовместных событий. Каждый такой исход называют элементарным событием (или элементарным исходом) и обозначают буквой w. Совокупность всех элементарных событий, которые могут появится в эксперименте, называют пространством элементарных событий и обозначают буквой W.
В теоретико-множественной трактовке любое событие А представляет собой некоторое подмножество А=<w> пространства элементарных событий W. Событие А происходит или нет в зависимости от того, принадлежит или нет подмножеству А элементарное событие w, представляющее исход данного опыта. Таким образом, событие А есть подмножество множества W, состоящее из элементарных исходов w, которые благоприятствуют событию А. Поэтому, в дальнейшем, не будем делать различий между событием А и соответствующим подмножеством АÌW.
Среди событий, являющихся подмножеством множества W, можно рассмотреть и само множество W; оно называется достоверным событием. Ко всему пространству W еще добавляется пустое множество Æ; это множество тоже рассматривается как событие и называется невозможным событием.
Для математической формализации модели случайного эксперимента требуется в первую очередь построить пространство элементарных событий W. Однако поскольку понятие «элементарный исход» строго не определено, то задача построения пространства элементарных событий допускает несколько решений. На практике построение такого множества осуществляется из требования, чтобы все интересующие нас результаты данного эксперимента однозначно описывались на основе построенного множества.
Пример 2.1. Пусть эксперимент состоит в подбрасывании один раз игральной кости. Обозначим через X число выпавших очков. Построить пространство элементарных событий W и указать состав подмножеств, соответствующих следующим событиям: A=
Решение. Очевидно, что за элементарные события здесь лучше всего взять события: <1>, <2>, <3>, <4>, <5>, <6>, которые образуют полную группу несовместных событий. При помощи этих элементарных событий можно легко описать все перечисленные в задаче события:
Отметим, что при решении вероятностных задач построение пространства элементарных событий играет большую роль. Если это пространство построено удачно, то решение задач может значительно упроститься; в противном случае она может представлять значительные трудности или даже вообще не будет найдено. Так, в рассматриваемой задаче за элементарные события можно было бы взять события: w1=
Алгебра событий
Поскольку при теоретико-множественном подходе к теории вероятностей события отождествляются с множествами, то над событиями можно совершать те же самые операции, что и для множеств. В частности:
| Алгебра событий | Алгебра множеств | ||
| AÌB | событие А влечет за собой событие В | AÌB | множество А является подмножеством множества В |
| A=B | событие А тождественно событию В | A=B | равенство множеств |
| A+B | сумма событий, означающее, что произошло хотя бы одно из двух событий | AÈB | объединение множеств |
| A×B | произведение событий, означающее, что оба события произойдут одновременно | AÇB | пересечение множеств |
| A–B | разность событий, означающее, что произойдет событие А, но не произойдет событие В | A B | разность множеств, т.е. множество элементов, принадлежащих А, но не принадлежащих В |
| =W–A | противоположное событие, означающее, что событие А не произойдет | =W A | дополнение множества А до W |
Если события А и В несовместны, то А×В=Æ; если события А1, А2, . Аk образуют полную группу, то А1+А2+. +Аk =W. В частности, противоположные события A и 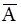 несовместны, т.е. А=Æ, и образуют полную группу, т.е. А+=W.
несовместны, т.е. А=Æ, и образуют полную группу, т.е. А+=W.
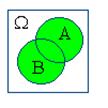
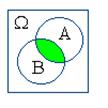
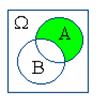
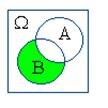
Действия над событиями становятся более наглядными, если придать им геометрическую интерпретацию в виде диаграмм Вьенна:
 |
 |
 |
 |
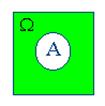 |
| A+B | AB | A–B | B–A | |
Пример 2.2. Эксперимент состоит в подбрасывании двух игральных костей. Обозначим через X сумму очков, выпадавших на обоих костях. Пространство элементарных событий такого эксперимента можно записать в виде W=<2;3;4;5;6;7;8;9;10;11;12>. Описать следующие события A+B, AB, A–B, B–A, если A=
| A+B=<3;5;6;7;9;11;12>, | A–B=<6;12>, |
| AB=<3;9>, | B–A=<5;7;11>. |
Пример 2.3. Пусть имеется колода карт, из которой вынимается одна карта. Описать события AB, B, A+B, A–B, если A=<вынутая карта – туз>, B=<вынутая карта – черви>.
Ответ:
Пример 2.3. Пусть A, B, C – три события, наблюдаемые в некотором эксперименте. Используя алгебру событий, описать следующие события: а) произошло только событие А; б) произошло одно событие; в) произошло хотя бы одно событие.
Ответ:
а) 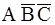 ,
,
б) 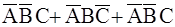 ,
,
в) A+B+C = 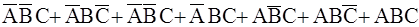 .
.
Операции сложения (объединения) и умножения (пересечения) события обладают рядом свойств, аналогичных свойствам обычных операций над числами:
| 1а. A+B = B+A, | 1б. AB = BA, |
| 2а. A+(B+C) = (A+B)+C, | 2б. A(BC) = (AB)C. |
Это свойства коммутативности и ассоциативности. При этом, пустое множество Æ и само базисное множество W аналогичны нулю и единице, соответственно:
| 3а. A+Æ = A, | 3б. AW = A. |
Однако некоторые свойства не имеют аналогов в обычных операциях над числами; в частности:
| 4а. A+A = A, | 4б. AA = A. |
Это свойства идемпотентности. При введении операций всегда возникает вопрос, какая из двух операций больше "похожа" на сложение, а какая на умножение. Ответ на этот вопрос дают свойства дистрибутивности. Однако для алгебры событий (соответственно, и для алгебры множеств) удивительным образом выполняются оба свойства дистрибутивности:
| 5а. (A+B)C = AC+BC, | 5б. (AB)+C = (A+C)(B+C). |
В теоретико-множественной трактовке эти свойства выглядят более симметрично:
| 5а. (AÈB)ÇC = (AÇC)È(BÇC), | 5б. (AÇB)ÈC = (AÈC)Ç(BÈC). |
Эти равенства характеризуют принцип двойственности алгебры событий и показывают равноправие обоих операций. Так, если будет доказана истинность какого-либо тождества, то истинным будет и двойственное ему тождество, т.е. то, которое получается из данного взаимной заменой символов «+» и «×» (или «È» и «Ç»), а также Æ и W. Поэтому все приводимые равенства сгруппированы в пары. Запишем еще несколько свойств:
| 6а. (AB)+A = A, | 6б. (A+B)A = A, | |
| 7а. A+ = W, | 7б. A = Æ, | |
| 8. ` = A, | ||
| 9а. `Æ = W, | 9а. `W = Æ, | |
| 10а. A+W = W, | 10б. AÆ = Æ, | |
11а. 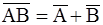 , , |
11б. 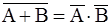 . . |
Законы де Моргана |
Система подмножеств множества W, обладающая приведенными свойствами, называется булевой алгеброй. К булевым алгебрам относятся алгебра множеств, алгебра событий и алгебра логики.
Пример 3.4. Покажите, что события A, 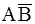 и
и 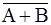 образуют полную группу несовместных событий.
образуют полную группу несовместных событий.
Решение. Покажем, что сумма данных событий образует достоверное событие. Используя законы де Моргана и другие свойства событий, получим:
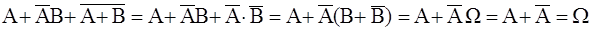 .
.
Следовательно, данные события образуют полную группу. Чтобы доказать несовместность данных событий, найдем их попарные произведения:
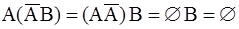 ,
,
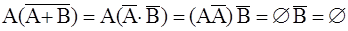 ,
,
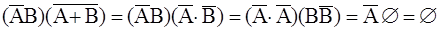 .
.
Таким образом, данные в задаче события попарно несовместны. Следовательно, эти события образуют полную группу несовместных события, т.е. образуют пространство элементарных событий.
Не все случайные явления (эксперименты) можно изучать методами теории вероятностей, а лишь те, которые могут быть воспроизведены в одних и тех же условиях. Случайность и хаос не одно и то же. Оказывается, что и в случайных экспериментах наблюдаются некоторые закономерности, например свойство «статистической устойчивости» : если некоторое событие, могущее произойти или не произойти в результате эксперимента, то доля экспериментов, в которых данное событие произошло, имеет тенденцию стабилизироваться с ростом общего числа экспериментов , приближаясь к некоторому числу . Это число служит объективной характеристикой «степени возможности» событию произойти.
Следует помнить, что мы занимаемся математикой и имеем дело не с реальностью, а лишь с её математической моделью. Мы и будем изучать только математические модели, а приложение их к реальности оставим на долю математической и практической статистики.
Примеры событий: выпало одно или два очка; выпало нечётное число очков.
Примеры событий:
при первом подбрасывании выпало одно очко;
при втором подбрасывании выпало одно очко;
на костях выпало одинаковое число очков;
на обеих костях выпало нечётное число очков.
1. Достоверным называется событие, которое обязательно происходит в результате эксперимента, т.е. единственное событие, включающее все элементарные исходы событие .
2. Невозможным называется событие, которое не может произойти в результате эксперимента, т.е. событие, не содержащее ни одного элементарного исхода («пустое множество» ). Заметим, что всегда .
1. Объединением событий и называется событие, состоящее в том, что произошло либо , либо , либо оба события одновременно. На языке теории множеств есть множество, содержащее как элементарные исходы из множества , так и элементарные исходы из множества .
2. Пересечением событий и называется событие, состоящее в том, что произошли оба события и одновременно. На языке теории множеств есть множество, содержащее элементарные исходы, входящие в пересечение множеств и .
3. Противоположным (или дополнительным) к событию называется событие , состоящее в том, что событие в результате эксперимента не произошло. Т.е. множество состоит из элементарных исходов, не входящих в .
4. Дополнением события до называется событие, состоящее в том, что произошло событие , но не произошло . Т.е. множество содержит элементарные исходы, входящие в множество , но не входящие в .
1. События и называют несовместными , если .
2. События называют попарно несовместными , если для любых , где , события и несовместны.
3. Говорят, что событие влечёт событие , и пишут , если всегда, как только происходит событие , происходит и событие . На языке теории множеств это означает, что любой элементарный исход, входящий в множество , одновременно входит и в множество , т.е. содержится в .
Так, эксперименты из примеров 1, 2 и 4 (но не 3) приводят к дискретным пространствам элементарных исходов.
Множество счётно , если существует взаимно-однозначное соответствие между этим множеством и множеством всех натуральных чисел. Счётными множествами являются, например, множество натуральных чисел, множество целых чисел, множество рациональных чисел, множество чётных чисел и т.д. Множество конечно , если оно состоит из конечного числа элементов.
Назовём число вероятностью элементарного исхода . Вероятностью события назовём число
равное сумме вероятностей элементарных исходов, входящих в множество . В случае положим .
2. Если и несовместны, то ;
3. В общем случае ;
Если событие состоит из элементарных исходов, то вероятность этого события равняется отношению :
где символом обозначено число элементов конечного множества .
называемой классическим определением вероятности.
Мы видим теперь, что подсчёт вероятности в классической схеме сводится к подсчёту общего числа «шансов» и числа шансов, благоприятствующих какому-либо событию. Число шансов считают с помощью формул комбинаторики.
Рассмотрим описанные в параграфе 1 урновые схемы. Три схемы: с возвращением и с учётом порядка, без возвращения и с учётом порядка, а также без возвращения и без учёта порядка, удовлетворяют классическому определению вероятности. Общее число элементарных исходов в этих схемах подсчитано в теоремах 4, 2, 3 и равно соответственно , , . Четвёртая же схема схема выбора с возвращением и без учёта порядка имеет заведомо неравновозможные исходы.
Если порядок не учитывать, то следует объявить два последних исхода одним и тем же результатом эксперимента, и получить не четыре, а три исхода:
Первые два исхода имеют вероятности по 1/4, а последний вероятность 1/4+1/4=1/2.
Решение. При или искомая вероятность равна нулю, так как соответствующее событие невозможно. Пусть и .
Результатом эксперимента является набор из шаров. Можно не учитывать или учитывать порядок следования шаров, вероятность не должна зависеть от способа подсчёта.
Выбор без учёта порядка. Общее число элементарных исходов есть число -элементных подмножеств множества, состоящего из элементов: (по теореме 3).
Обозначим через событие, вероятность которого требуется найти. Событию благоприятствует появление любого набора, содержащего белых шаров и чёрных. Число благоприятных исходов равно произведению (по теореме 1) числа способов выбрать белых шаров из и числа способов выбрать чёрных шаров из , т.е. . Вероятность события равна
Выбор с учётом порядка. Общее число элементарных исходов есть число способов разместить элементов на местах: по теореме 2,
При подсчёте числа благоприятных исходов нужно учесть число способов выбрать белых и чёрных шаров и число способов расположить эти шары среди . Можно, скажем, посчитать число способов выбрать мест среди (равное ), затем число способов разместить на этих местах белых шаров (равное ), и затем число способов разместить на оставшихся местах чёрных шаров (равное ). Перемножив ( почему?) эти числа, получим
(где таково, что , и ) называется гипергеометрическим распределением .
В гипергеометрическом распределении единичная вероятность распределена между подходящими целыми числами неравномерно. Каждому целому числу сопоставлена своя вероятность . На вещественной прямой можно единичную вероятность распределить по-разному. Этим одно распределение отличается от другого: тем, на каком множестве чисел «распределена» общая единичная вероятность, и тем, какие веса, или вероятности, присвоены отдельным точкам или частям этого множества.
1 Jacob Bernoulli (27.12.1654 16.08.1705, Basel, Switzerland) .
