Вход: Регулярная грамматика  .
.
Выход: КА  .
.
Шаг 1. Пополнить грамматику правилом  , где
, где  и
и  — новый нетерминал, для каждого правила вида
— новый нетерминал, для каждого правила вида  , если в грамматике нет соответствующего ему правила
, если в грамматике нет соответствующего ему правила  , где
, где  .
.
Шаг 2. Начальный символ грамматики  принять за начальное состояние КА
принять за начальное состояние КА  . Из нетерминалов образовать множество состояний автомата
. Из нетерминалов образовать множество состояний автомата  , а из терминалов – множество символов входного алфавита
, а из терминалов – множество символов входного алфавита  .
.
Шаг 3. Каждое правило  преобразовать в функцию переходов
преобразовать в функцию переходов  , где
, где  .
.
Шаг 4. Во множество заключительных состояний включить все вершины, помеченные символами  из правил вида
из правил вида  , для которых имеются соответствующие правила
, для которых имеются соответствующие правила  , где
, где  .
.
Шаг 5. Если в грамматике имеется правило  , где
, где  — начальный символ грамматики, то поместить
— начальный символ грамматики, то поместить  во множество заключительных состояний.
во множество заключительных состояний.
Шаг 6. Если получен НКА, то преобразовать его в ДКА.
ПримерДана регулярная грамматика  с правилами
с правилами 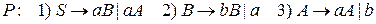 . Построить по регулярной грамматике конечный автомат.
. Построить по регулярной грамматике конечный автомат.
Решение задачи состоит из следующей последовательности действий.
1 Построим по регулярной грамматике КА.
1.1 Пополним грамматику правилами  и
и  , где
, где  — новый нетерминал.
— новый нетерминал.
1.2 Начальное состояние конечного автомата  . Множество состояний автомата
. Множество состояний автомата 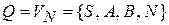 , множество символов входного алфавита
, множество символов входного алфавита  .
.
1.3 Значения сформированной функции переходов даны в таблице 2.7.
Таблица 2.7 – Функция переходов автомата 
 |
S | A | B | N |
| a | A, B | A | N |  |
| b |  |
N | B |  |
1.4 Множество заключительных состояний  .
.
1.5 Для начального символа грамматики e-правила отсутствуют.
Конечный автомат М — недетерминированный, граф НКА представлен на рисунке 2.5.
 |
Рисунок 2.5 — Граф НКА
Контекстно-свободные языки и грамматики
Задача разбора
Вывод цепочек
Выводом называется процесс порождения предложения языка на основе правил определяющей язык грамматике. Чтобы дать формальное определение процессу вывода, необходимо ввести еще несколько дополнительных понятий.
ОпределениеЦепочка b Î (VTÈVN) * непосредственно выводима из цепочки  в грамматике
в грамматике  (обозначается:aÞb), если
(обозначается:aÞb), если 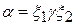 и
и  , где
, где  ,
,  и правило вывода
и правило вывода 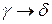 содержится во множестве Р.
содержится во множестве Р.
Определение Цепочка b Î (VTÈVN) * выводима из цепочки  в грамматике
в грамматике  (обозначается aÞ*b), если существует последовательность цепочек
(обозначается aÞ*b), если существует последовательность цепочек  (n³) такая, что
(n³) такая, что  .
.
Такая последовательность непосредственно выводимых цепочек называется выводом или цепочкой вывода.
Вывод называется правосторонним (левосторонним), если в нем на каждом шаге вывода правило грамматики применяется всегда к крайнему правому (левому) нетерминальному символу в цепочке.
Вывод можно рассматривать также как процесс получения одной строки из другой. С понятием вывода тесно связано понятие разбора строки языка. С одной стороны, разбор— это задача выяснения принадлежности заданной строки языку, порождаемому заданной грамматикой. С другой стороны, разбор — это последовательность правил грамматики, определенным образом соответствующая выводу.
В грамматике G1 SÞ*000111, т.к. существует вывод  .
.
Дерево разбора
Графическим способом отображения процесса разбора цепочек является дерево разбора (или дерево вывода).
Определение дерево разбора грамматики  называется дерево, которое соответствует некоторой цепочке вывода и удовлетворяет следующим условиям:
называется дерево, которое соответствует некоторой цепочке вывода и удовлетворяет следующим условиям:
— каждая вершина дерева обозначается символом грамматики 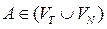 ;
;
— корнем дерева является вершина, обозначенная начальным символом грамматики S;
— листьями дерева (концевыми вершинами) являются вершины, обозначенные терминальными символами грамматики или символом пустой строки e;
— если некоторый узел дерева обозначен символом  , а связанные с ним узлы – символами
, а связанные с ним узлы – символами  , то в грамматике
, то в грамматике  существует правило
существует правило 
Дерево разбора можно построить двумя способами: сверху вниз и снизу вверх.
Нисходящее дерево разбора
При построении дерева вывода сверху вниз построение начинается с целевого символа грамматики, который помещается в корень дерева. Затем в грамматике выбирается необходимое правило, и на первом шаге вывода корневой символ раскрывается на несколько символов первого уровня. На втором шаге среди всех концевых вершин дерева выбирается крайняя (крайняя левая — для левостороннего вывода, крайняя правая — для правостороннего) вершина, обозначенная нетерминальным символом, для этой вершины выбирается нужное правило грамматики, и она раскрывается на несколько вершин следующего уровня. Построение дерева заканчивается, когда все концевые вершины обозначены терминальными символами, в противном случае надо вернуться ко второму шагу и продолжить построение.
Восходящее дерево разбора
Построение дерева вывода снизу вверх начинается с листьев дерева. В качестве листьев выбираются терминальные символы конечной цепочки вывода, которые на первом шаге построения образуют последний уровень (слой) дерева. Построение дерева идет по слоям. На втором шаге построения в грамматике выбирается правило, правая часть которого соответствует крайним символам в слое дерева (крайним правым символам при правостороннем выводе и крайним левым — при левостороннем). Выбранные вершины слоя соединяются с новой вершиной, которая выбирается из левой части правила. Новая вершина попадает в слой де рева вместо выбранных вершин. Построение дерева закончено, если достигнута корневая вершина (обозначенная целевым символом), а иначе надо вернуться ко второму шагу и повторить его над полученным слоем дерева.
Поскольку все известные языки программирования имеют нотацию записи «слева — направо», компилятор также всегда читает входную программу слева направо (и сверху вниз, если программа разбита на несколько строк). Поэтому для построения дерева вывода методом «сверху вниз», как правило, используется левосторонний вывод, а для построения «снизу вверх» — правосторонний вывод. На эту особенность компиляторов стоит обратить внимание. Нотация чтения программ «слева направо» влияет не только на порядок разбора программы компилятором (для пользователя это, как правило, не имеет значения), но и ни порядок выполнения операций — при отсутствии скобок большинство равноправных операций выполняются в порядке слева направо, а это уже имеет существенное значение.
Однозначность грамматик
Грамматика называется однозначной, если для каждой цепочки символов языка, заданного этой грамматикой, можно построить единственный левосторонний (и единственный правосторонний) вывод. Или, что то же самое: грамматика называется однозначной, если для каждой цепочки символов языка, заданного этой грамматикой, существует единственное дерево вывода. В противном случае грамматика называется неоднозначной.
3.2 Преобразование КС-грамматик
ОпределениеКС-грамматика называется приведенной, если она не имеет циклов, e-правил и бесполезных символов.
Рассмотрим основные алгоритмы приведения КС-грамматик.
Перед всеми другими исследованиями и преобразованиями КС-грамматик выполняется проверка существования языка грамматики.
Вход: Регулярная грамматика  .
.
Выход: КА 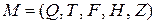 .
.
Шаг 1. Пополнить грамматику правилом 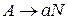 , где
, где 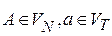 и
и  — новый нетерминал, для каждого правила вида
— новый нетерминал, для каждого правила вида 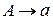 , если в грамматике нет соответствующего ему правила
, если в грамматике нет соответствующего ему правила  , где
, где  .
.
Шаг 2. Начальный символ грамматики 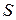 принять за начальное состояние КА
принять за начальное состояние КА 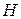 . Из нетерминалов образовать множество состояний автомата
. Из нетерминалов образовать множество состояний автомата  , а из терминалов – множество символов входного алфавита
, а из терминалов – множество символов входного алфавита  .
.
Шаг 3. Каждое правило  преобразовать в функцию переходов
преобразовать в функцию переходов 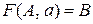 , где
, где  .
.
Шаг 4. Во множество заключительных состояний включить все вершины, помеченные символами  из правил вида
из правил вида  , для которых имеются соответствующие правила
, для которых имеются соответствующие правила 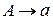 , где
, где  .
.
Шаг 5. Если в грамматике имеется правило 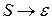 , где
, где  — начальный символ грамматики, то поместить
— начальный символ грамматики, то поместить  во множество заключительных состояний.
во множество заключительных состояний.
Шаг 6. Если получен НКА, то преобразовать его в ДКА.
ПримерДана регулярная грамматика 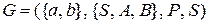 с правилами
с правилами 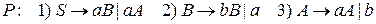 . Построить по регулярной грамматике конечный автомат.
. Построить по регулярной грамматике конечный автомат.
Решение задачи состоит из следующей последовательности действий.
1 Построим по регулярной грамматике КА.
1.1 Пополним грамматику правилами  и
и  , где
, где  — новый нетерминал.
— новый нетерминал.
1.2 Начальное состояние конечного автомата 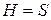 . Множество состояний автомата
. Множество состояний автомата  , множество символов входного алфавита
, множество символов входного алфавита  .
.
1.3 Значения сформированной функции переходов даны в таблице 2.7.
Таблица 2.7 – Функция переходов автомата 
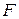 |
S | A | B | N |
| a | A, B | A | N | 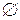 |
| b | 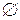 |
N | B |  |
1.4 Множество заключительных состояний  .
.
1.5 Для начального символа грамматики e-правила отсутствуют.
Конечный автомат М — недетерминированный, граф НКА представлен на рисунке 2.5.
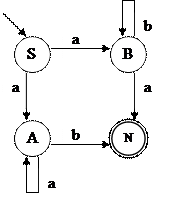 |
Рисунок 2.5 — Граф НКА
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Как то на паре, один преподаватель сказал, когда лекция заканчивалась — это был конец пары: "Что-то тут концом пахнет". 8513 —  | 8099 —
| 8099 —  или читать все.
или читать все.
91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
О языке говорят, что он допускается (или воспринимается) конечным автоматом . О любой цепочке, принадлежащей языку , говорят, что она допускается (или воспринимается) конечным автоматом . Такую цепочку называют также допустимой цепочкой данного конечного автомата.
Определение 7.10. Два конечных автомата и называют эквивалентными, если их языки совпадают:
Установим теперь связь между понятиями конечного автомата и регулярной грамматики.
Теорема 7.5. Язык допускается конечным автоматом тогда и только тогда, когда он порождается регулярной грамматикой.
Чтобы доказать теорему, нужно:
1) указать способ построения регулярной грамматики по заданному конечному автомату , такой, чтобы язык, порождаемый грамматикой , совпадал с языком, допускаемым автоматом ;
2) указать способ построения конечного автомата по заданной регулярной грамматике , такой, чтобы язык, допускаемый автоматом , совпадал с языком, порождаемым грамматикой .
Замечание 7.9. Регулярную грамматику и конечный автомат , такие, что , иногда называют эквивалентными.
Рассмотрим эти построения по очереди.
Построение регулярной грамматики по конечному автомату
Пусть дан конечный автомат
Определим регулярную грамматику следующим образом: терминальный алфавит совпадает с входным алфавитом автомата ; нетерминальный алфавит находится во взаимно однозначном соответствии с множеством состояний автомата , причем состоянию сопоставлен нетерминал и аксиома сопоставлена начальному состоянию , то есть ; множество правил вывода строится по системе команд так: правило вывода , где , принадлежит тогда и только тогда, когда в есть команда ; кроме того, если (и только если) состояние заключительное , то в добавляется правило вывода . Если же (и только в этом случае), то в помещаем правило вывода .
Для конечного автомата на рис. 7.5 получим следующую регулярную грамматику:
Заметим, что, читая цепочку в автомате, в грамматике мы ее выводим (порождаем). Например,
Докажем, что описанное построение корректно, т.е. . Для этого сначала, используя индукцию по длине пути в конечном автомате , докажем, что из факта достижимости в автомате (для любого ) следует выводимость в грамматике для любых и .
Пусть длина пути , то есть и . Так как метка пути нулевой длины в ориентированном графе, размеченном над полукольцом , равна единице полукольца — регулярному выражению , то при . Но выполняется тривиально.
Пусть для любого из достижимости следует выводимость , и пусть в автомате существует путь длины , ведущий из вершины в вершину , на котором читается цепочка , то есть . Так как длина пути не меньше 1, то в нем есть по крайней мере одна дуга и существуют такая вершина и такое , что , где (мы выделили первую дугу пути ). Тогда, согласно построению множества правил вывода грамматики , в содержится правило , а, по предположению индукции, из того, что в имеется , следует, что . В итоге получаем , то есть , что и требовалось.
Теперь если цепочка , то в существует путь, ведущий из начального состояния в одно из заключительных состояний , на котором читается цепочка , то есть некоторого . Если и тогда , то в множестве правил вывода есть правило и . Если же отлично от , то, какова бы ни была цепочка , путь из в , на котором она читается, имеет длину, не меньшую единицы. Выделяя в этом пути последнюю дугу, получим , где . Но тогда, во-первых, как мы только что доказали, в грамматике имеет место выводимость , а, во-вторых, из того, что , согласно построению множества правил вывода грамматики , следует, что в ней есть правило , и окончательно получим
Таким образом, мы полностью доказали, что для каждой цепочки из того, что , следует , т.е. имеет место включение .
Чтобы доказать обратное включение, используя индукцию по длине вывода в грамматике , покажем сначала, что из факта выводимости (для любого ) следует достижимость в автомате для любых и .
При имеем и тривиально выполняется .
Пусть для любого из выводимости следует достижимость (в автомате ), и пусть в грамматике существует вывод длины цепочки из цепочки , то есть . Так как длина вывода не меньше 1, то найдется такой нетерминал и такое , что , где (мы выделили первый шаг вывода ). Непосредственная выводимость означает, что в множестве правил вывода грамматики содержится правило и, следовательно, в системе команд конечного автомата есть команда и тогда . Согласно предположению индукции, из того, что , следует, что в . В итоге получаем , т.е., так как , что и требовалось.
Если теперь , то в грамматике существует вывод цепочки из аксиомы , то есть . На последнем шаге этого вывода применяется некоторое правило, правая часть которого не содержит вхождений нетерминалов, т.е. правило вида . Поскольку любая цепочка в выводе в регулярной грамматике может содержать нетерминал только как последний символ, то . Отсюда следует, что . Кроме того, правило вывода может принадлежать множеству тогда и только тогда (по построению ), когда в системе команд автомата есть команда . Следовательно, , что и означает , то есть .
Итак, доказано включение , и , т.е. регулярная грамматика , построенная, как описано выше, по конечному автомату , эквивалентна ему.
Построение конечного автомата по регулярной грамматике
По заданной регулярной грамматике
построим конечный автомат так, что входной алфавит автомата совпадает с терминальным алфавитом грамматики , множество состояний совпадает с нетерминальным алфавитом грамматики , пополненным новым состоянием , не принадлежащим объединенному алфавиту грамматики , то есть ; начальное состояние совпадает с аксиомой , множество заключительных состояний >. Система команд определяется следующим образом: команда принадлежит тогда и только тогда, когда в множестве правил вывода есть правило , а команда принадлежит тогда и только тогда, когда правило вывода принадлежит множеству .
Например, по регулярной грамматике из примера 7.5 строится конечный автомат с входным алфавитом , множеством состояний , начальным состоянием , единственным заключительным состоянием и такой системой команд (рис. 7.6):
Обоснование корректности этого построения может быть проведено так же, как и построения регулярной грамматики по конечному автомату ("двойной" индукцией по длине вывода в грамматике и по длине пути в автомате), и мы его опускаем.
Таким образом, конечные автоматы допускают в точности те же языки, которые порождают регулярные грамматики.
