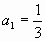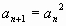Содержание
такая последовательность  что для всех
что для всех  выполняется неравенство
выполняется неравенство  Иногда такие последовательности наз. строго возрастающим и, а термин "В. п." применяется к последовательностям, удовлетворяющим для всех плишь условию
Иногда такие последовательности наз. строго возрастающим и, а термин "В. п." применяется к последовательностям, удовлетворяющим для всех плишь условию  Такие последовательности наз. также неубывающими. Всякая ограниченная сверху неубывающая последовательность имеет конечный предел, а всякая не ограниченная сверху имеет бесконечный предел, равный +бесконечн. Л. Д. Кудрявцев.
Такие последовательности наз. также неубывающими. Всякая ограниченная сверху неубывающая последовательность имеет конечный предел, а всякая не ограниченная сверху имеет бесконечный предел, равный +бесконечн. Л. Д. Кудрявцев.
Математическая энциклопедия. — М.: Советская энциклопедия . И. М. Виноградов . 1977—1985 .
Смотреть что такое "ВОЗРАСТАЮЩАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ" в других словарях:
возрастающая последовательность — — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом EN ascending sequence … Справочник технического переводчика
Возрастающая подпоследовательность — Задача поиска наибольшей увеличивающейся подпоследовательности состоит в отыскании наиболее длинной возрастающей подпоследовательности в данной последовательности элементов. Содержание 1 Постановка задачи 2 Родственные алгоритмы … Википедия
Возрастающая функция — Монотонная функция это функция, приращение которой не меняет знака, то есть либо всегда неотрицательно, либо всегда неположительно. Если в дополнение приращение не равно нулю, то функция называется строго монотонной. Содержание 1 Определения 2… … Википедия
Числовая последовательность — Последовательность Числовая последовательность это последовательность элементов числового пространства. Числовые пос … Википедия
Монотонная последовательность — это последовательность, элементы которой с увеличением номера не убывают, или, наоборот, не возрастают. Подобные последовательности часто встречаются при исследованиях и имеют ряд отличительных особенностей и дополнительных свойств.… … Википедия
Монотонность последовательности — Монотонная последовательность последовательность , удовлетворяющая одному из следующих условий: для любого номера выполняется неравенство (неубывающая последовательность), для любого номера выполняется неравенство (невозрастающая… … Википедия
МЕТРИЧЕСКАЯ ТЕОРИЯ ЧИСЕЛ — раздел теории чисел, в к ром изучаются и метрически (т. е. на основе теории меры )характеризуются множества чисел, обладающих определенными арифметич. свойствами. М. т. ч. тесно связана с теорией вероятностей, что иногда дает возможность… … Математическая энциклопедия
Теорема Вейерштрасса об ограниченной возрастающей последовательности — утверждает, что любая ограниченная возрастающая последовательность имеет предел, причем этот предел равен ее точной верхней грани. Несмотря на простоту доказательства, эта теорема оказывается очень удобной для нахождения пределов многих… … Википедия
МАННА ТЕОРЕМА — теорема, дающая оценку плотности суммы двух последовательностей. Пусть А= <0, а 1, а.2,. . ., а i, . >возрастающая последовательность целых чисел и Плотностью последовательности Аназ. величина А р и ф м е т и ч е с к о й суммой двух… … Математическая энциклопедия
ОБОБЩЕННЫХ ФУНКЦИЙ ПРОСТРАНСТВО — пространство, сопряженное к пространству основных (достаточно хороших) функций. Важную роль здесь играют Фреше пространства (типа FS )и сильно сопряженные к ним (типа DFS). Пространство типа FS есть проективный предел компактной… … Математическая энциклопедия
 Числовые последовательности. Способы задания числовых последовательностей Числовые последовательности. Способы задания числовых последовательностей |
 Возрастающие и убывающие последовательности Возрастающие и убывающие последовательности |
 Ограниченные и неограниченные последовательности Ограниченные и неограниченные последовательности |

Числовые последовательности. Способы задания числовых последовательностей
Если каждому натуральному числу n поставлено в соответствие некоторое действительное число xn , то говорят, что задана числовая последовательность
Число x1 называют членом последовательности с номером 1 или первым членом последовательности , число x2 — членом последовательности с номером 2 или вторым членом последовательности, и т.д. Число xn называют членом последовательности с номером n .
Существуют два способа задания числовых последовательностей – с помощью формулы общего члена последовательности и с помощью рекуррентной формулы .
Задание последовательности с помощью формулы общего члена последовательности – это задание последовательности
с помощью формулы, выражающей зависимость члена xn от его номера n .
Пример 1 . Числовая последовательность
задана с помощью формулы общего члена
Задание последовательности с помощью формулы, выражающей член последовательности xn через члены последовательности с предшествующими номерами, называют заданием последовательности с помощью рекуррентной формулы .
Пример 2 (Числа Фибоначчи). Числовая последовательность
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, …
может быть задана с помощью рекуррентной формулы
с начальными условиями
Возрастающие и убывающие последовательности
называют возрастающей последовательностью, если каждый член этой последовательности больше предшествующего члена.
Другими словами, для всех n = 1, 2, 3, … выполнено неравенство
Пример 3 . Последовательность натуральных чисел
является возрастающей последовательностью.
называют убывающей последовательностью, если каждый член этой последовательности меньше предшествующего члена.
Другими словами, для всех n = 1, 2, 3, … выполнено неравенство
xn + 1 Пример 4 . Последовательность
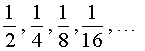
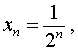
является убывающей последовательностью.
Пример 5 . Числовая последовательность
не является ни возрастающей, ни убывающей последовательностью.
Определение 3. Возрастающие и убывающие числовые последовательности называют монотонными последовательностями .
Ограниченные и неограниченные последовательности
называют ограниченной сверху, если существует такое число M, что каждый член этой последовательности меньше числа M .
Другими словами, для всех n = 1, 2, 3, … выполнено неравенство
называют ограниченной снизу, если существует такое число m, что каждый член этой последовательности больше числа m .
Другими словами, для всех n = 1, 2, 3, … выполнено неравенство
называют ограниченной, если она ограничена и сверху, и снизу.
Другими словами, существуют такие числа M и m, что для всех n = 1, 2, 3, … выполнено неравенство
m Определение 7. Числовые последовательности, которые не являются ограниченными, называют неограниченными последовательностями .
Пример 6 . Числовая последовательность
ограничена снизу, например, числом 0. Однако эта последовательность неограничена сверху.
Пример 7 . Последовательность
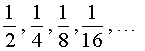
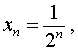
является ограниченной последовательностью, поскольку для всех n = 1, 2, 3, … выполнено неравенство
Разделы: Математика
Цель: Дать понятие, определение последовательности, конечной, бесконечной, различные способы задания последовательностей, их различие, научить применять при решении примеров.
I. Организационный момент.
II. Фронтальная проверка домашнего задания:
1) ученик на доске задачу № 2.636 (из II части “Сборника заданий для письменного экзамена в 9 кл.)
2) ученик. Построить график
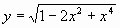
3) фронтально со всем классом № 2.334 (а).
III. Объяснение нового материала.
Школьная лекция – это такая форма организации учебного процесса, которая ориентирует учащихся при изучении той или иной темы на главное и предполагает широкую демонстрацию личностного отношения учителя и учащихся к учебному материалу. Т.к. урок-лекция предусматривает крупноблочное изложение учителем материала, то речевое общение учителя и учащихся является главным в ее технологии. Слово учителя оказывает эмоциональное, эстетическое воздействие и создает определенное отношение к предмету. С помощью лекции осуществляется руководство различными видами деятельности учащихся на занятии, а через знания, умения и навыки формируется познание как основа учебной деятельности.
I. Выпишите в порядке возрастания двузначные числа, оканчивающиеся цифрой 3.
Каждому порядковому номеру от 1 до 9 поставьте в соответствие определенное двузначное число:
Между множеством первых девяти натуральных чисел и множеством двузначных чисел, оканчивающихся цифрой 3, установилось соответствие. Это соответствие является функцией.
Областью определения служит
Если соответствие обозначить f, то
| f (1)=13; | f (2)=23; | f (9)=93. |
Функция, область определения которой – множество натуральных чисел или множество первых n натуральных чисел, называется последовательностью.
Конечная последовательность – это функция, заданная на множестве первых n натуральных чисел.
| а) 3; 5; 7; 9 | о.о.ф. |
| м.з.ф. <3;5;7;9>. |
Эту последовательность можно задать с помощью пар.
II. 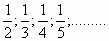
М.з.ф. 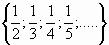 g(1) = g(1) = 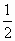 ; ; |
g(3) =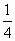 ; … ; … |
g(60) = 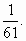 |
Функция, заданная на множестве натуральных чисел, называется бесконечной последовательностью.
1 —> 2; 2 —> 4; ……. n —> 2n
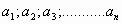 — члены последовательности.
— члены последовательности.
Замечание: следует различать понятие множества и понятие последовательности.
— одно и то же множество.
б) однако, последовательности 10; 20; 30; 40
(1; 10) (2;20) (3;30) (4;40)
(1; 40) (2;30) (3;20) (4;10).
III. Рассмотрим последовательность:
1) 3; 5; 7; 9; 11;……. —> бесконечная, возрастающая
2) 10; 9; 8; 7; 6. —> конечная, убывающая.
а) 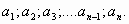
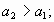
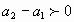 ;
; 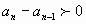
Последовательность называется возрастающей, если каждый член ее, начиная со второго, больше своего предыдущего.
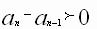
б) 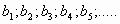
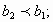
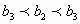 ;
; 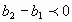
Дается определение убывающей последовательности.
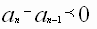
Возрастающие или убывающие последовательности называются монотонными.
1; 0; 1; 0; 1; 0. — колеблющаяся;
5; 5; 5; 5; ….. — постоянная.
IV. Последовательности можно изобразить геометрически. Т.к. последовательности – это функция, областью определения которой служит множество N, то графиком, видимо, является множество точек плоскости (х; у).
Пример: -3; -2; -1; 0; 1; 2; 3.
(1; -3) (2;-2) (3; -1) (4; 0) (5;1) (6;2) (7;3)
Построим график этой последовательности
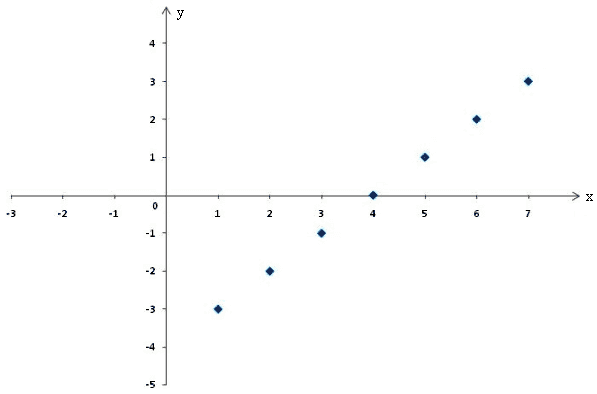
Пример: Докажите, что последовательность, заданная в таком виде
V. Способы задания последовательностей.
Т.к. последовательность – это функция, определенная на множестве N, то существует пять способов задания последовательностей:
II. Способ описания
I. Табличный – очень неудобный. Составляем таблицу и по ней определяем, какой член? какое место он занимает……..
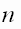 |
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
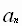 |
1 | 4 | 9 | 16 | 25 | 36 | 49 | 64 | 81 | 100 | 121 | 144 | 169 |
II. Способ описания.
Пример: Последовательность такова, что каждый ее член записывается с помощью цифры 4, и число цифр равно номеру числа последовательности.
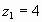 ;
; 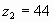 ;
; 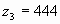 .
.
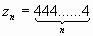
III. Аналитический способ ( с помощью формулы).
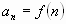
пример: 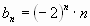
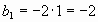
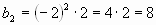

Формула, выражающая каждый член последовательности через его номер n, называется формулой n члена последовательности.
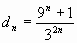
2) 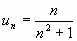
и ученики составляют эти последовательности, и наоборот: подберите формулу для членов последовательностей:
а) 1; 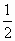 ; ; 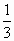 ;………….. ;………….. |
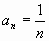 |
б) 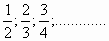 . . |
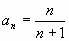 |
в) 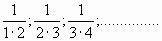 |
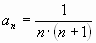 |
г) 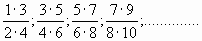 |
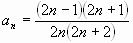 |
| д) 1;-2;3;-4;5;-6;…………. | 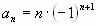 |
IV. Графический способ – тоже не очень удобный, обычно им и не пользуются.
Ученики должны четко знать, что соединять точки графика нельзя!
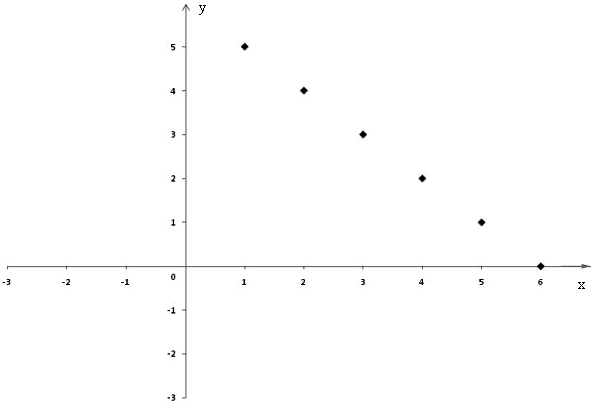
V. Рекуррентный способ.
Пример: В последовательности каждый член, начиная со второго, равен квадрату предшествующего.
Можно составить сколько угодно таких последовательностей:
в) 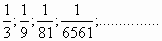
Здесь мы не знаем 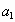 , поэтому достаточно указать первый член.
, поэтому достаточно указать первый член.
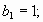
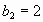 , а каждый член, начиная с третьего, равен сумме двух предшествующих членов.
, а каждый член, начиная с третьего, равен сумме двух предшествующих членов.
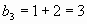
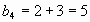
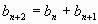
Формулу, выражающую любой член последовательности, начиная с некоторого, через предшествующие члены, называют рекуррентной.
Итак, еще раз обратить внимание учеников на то, что если последовательность задана рекуррентным способом, то:
1) обязательно известен первый член последовательности;
2) дана формула, позволяющая определить любой член последовательности по известным предшествующим членам.
1) 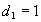 , а каждый член, начиная со второго, равен произведению своего номера и предыдущего числа.
, а каждый член, начиная со второго, равен произведению своего номера и предыдущего числа.
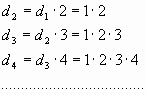
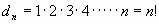 (Факториал).
(Факториал).
2) 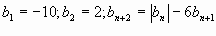
Напишите первые шесть членов последовательности.
На дом: из учебника Галицкого М.Л., Гольдмана А.М., Звавича Л.И. “Сборник задач по алгебре 8-9 кл.”
Стр.163 №№ 12.1 (г, д, е, ж), 12.2 (г, д, е), 12.4 (з, и, л), 12.5 (б,г).
Из сборника заданий 9 кл. (экзаменационный материал) № 2.641 (а).
Примечание: Начиная следующее занятие, можно ученикам дать понятие последовательности, ограниченной снизу, сверху, и решать задачи.