Содержание
Курсовая работа
по курсу «Дискретная математика»
Тема: Разработка алгоритма и программного обеспечения для решения прикладной задачи теории графов
Вариант №…
Содержание курсовой работы
Пояснительная записка к курсовой работе должна содержать следующие разделы:
· описание алгоритма решения поставленной задачи;
· ручной просчет (на небольшом примере показать работу алгоритма);
· список использованной литературы;
ЗАДАНИЯ К КУРСОВОЙ РАБОТЕ
Раздел 1. Некоторые базисные алгоритмы обработки графов
Нахождение минимального пути в графе
Путь в орграфе D из вершины v в вершину w, где v ¹ w, называется минимальным, если он имеет минимальную длину среди всех путей орграфа D из v в w.
Назовем орграф D = (V,X) нагруженным, если на множестве дуг X определена некоторая функция l : X ® R, которую часто называют весовой функцией. Значение l(x) будем называть длиной дуги x. Предположим, что l(x) ³ 0. Длиной пути П в нагруженном орграфе будем называть величину l(П), равную сумме длин дуг, входящих в П, при этом каждая дуга учитывается столько раз, сколько она входит в данный путь.
Нагруженный орграф можно задать с помощью матрицы весов С(D) = <cij>nxn с элементами
 l(vi,vj), если (vi,vj) ÎX,
l(vi,vj), если (vi,vj) ÎX,
ЗАДАНИЕ 1. Найти минимальные пути от фиксированной вершины до произвольной вершины графа, используя алгоритм Дейкстры.
Рассмотрим алгоритм Дейкстры, который позволяет определить минимальный путь в орграфе между двумя заданными вершинами при условии, что этот путь существует.
Пусть s – начальная вершина, t – конечная вершина. На каждой итерации любая вершина v имеет метку l * (v), которая может быть постоянной или временной. Постоянная метка l * (v) – это длина кратчайшего пути от s к v, временная метка l(v) – это вес кратчайшего пути из s в v, проходящий через вершины с постоянными метками. Если на каком-то шаге метка становится постоянной, то она остается такой до конца работы алгоритма.
Вторая метка Q(v) – это вершина, из которой вершина v получила свою метку.
А л г о р и т м Д е й к с т р ы
Данные: матрица весов С(D) орграфа D, начальная вершина s.
Результат: расстояния от вершины s до всех вершин орграфа D: D[v] = d(s,v), v Î V, а также последовательность вершин, определяющая кратчайший путь из s в v .
1. Положим l * (s) = 0 и будем считать эту метку постоянной. Для всех v ÎV, v ¹ s, положим l * (v) = ¥ и будем считать эти метки временными. Положим p = s.
2. Для всех vÎГp с временными метками выполним: если l * (v)>l * (p)+l(p,v), то l * (v)=l * (p)+l(p,v) и Q(v) =р. Иначе l * (v) и Q(v) не менять, т.е. l * (v) = min (l * (t), l * (p)+cpv). (Идея состоит в следующем: пусть p – вершина, получившая постоянную метку l * (p) на
предыдущей итерации. Просматриваем все вершины vÎГp, имеющие временные метки. Метка l * (v) вершины vÎГp заменяется на l * (p)+l(p,v), если оказывается, что ее метка l * (v)>l * (p)+l(p,v). В этом случае говорим, что вершина v получила свою метку из вершины p, поэтому положим Q(v) = p. С помощью этих дополнительных меток будем потом восстанавливать сам путь. Если l * (v) £ l * (p)+cpv, то метки остаются прежними.
3. Пусть V* — множество вершин с временными метками. Найдем вершину v* такую, что l * (v*) = min l * (v), v Î V*. Считать метку l * (v*) постоянной для вершины v*.
4. Положим p = v*. Если p = t, то перейдем к п.5 ( l * (t) – длина минимального пути ). Иначе перейдем к п.2.
5. Найдем минимальный путь из s в t, используя метки Q(v): П = s…Q(t)t.
Заметим, что, если продолжить работу алгоритма Дейкстры до тех пор, пока все вершины не получат постоянные метки, то мы получим расстояния от начальной вершины s до произвольной вершины графа.
ЗАДАНИЕ 2. Найти минимальные пути от фиксированной вершины до произвольной вершины графа, используя алгоритм Форда-Беллмана.
Большинство известных алгоритмов нахождения расстояния между двумя фиксированными вершинами s и t опираются на действия, которые в общих чертах можно представить следующим образом: при данной матрице весов дуг C вычисляются некоторые верхние ограничения D[v] на расстояния от s до всех вершин vÎV. Каждый раз, когда мы устанавливаем, что D[u] + cuv
Процесс прерывается, когда дальнейшее улучшение ни одного из ограничений невозможно. Можно показать, что значение каждой из переменных D[v] равно тогда d(s,v) — расстоянию от s до v. Заметим, что для того, чтобы определить расстояние от s до t, мы вычисляем здесь расстояния от s до всех вершин графа. Описанная общая схема является неполной, т.к. она не определяет очередности, в которой выбираются вершины u и v. Эта очередность оказывает сильное влияние на эффективность алгоритма. Опишем алгоритм Форда-Беллмана для нахождения расстояния от фиксированной точки s до всех остальных вершин графа.
А л г о р и т м Форда – Беллмана
Данные: матрица весов С(D) орграфа D, начальная вершина s.
Результат: расстояния от вершины s до всех вершин орграфа D: D[v] = d(s,v), v Î V.
1. Всем вершинам vÎV орграфа присвоим метку D[v] = csv. Вершине s присвоим метку D[s] = 0.
3. Выберем произвольную вершину vÎ V <s>.
4. Выберем произвольную вершину u ÎV.
6. Если вершина u пробежала еще не все множество вершин V, то выбрать среди оставшихся произвольную вершину и вернуться к шагу 5.
7. Если вершина v пробежала еще не все множество вершин V <s>, то выбрать среди оставшихся произвольную вершину и перейти к шагу 4.
8. Если k (0)
Аналогично корректируются метки всех оставшихся вершин, а именно,
Т.к. метки вершин изменились, то продолжаем процесс дальше. Результаты третьей и четвертой итераций совпали, значит итерационный процесс можно закончить, кроме того k = n-2 = 4.
Величины, стоящие в последнем столбце, и дают длины минимальных путей из вершины v1 до всех остальных вершин. Например, длина минимального пути из v1 в v2 равна 5, сам путь имеет вид: v1v5v3v2.
ЗАДАНИЕ 3. Найти минимальные пути между всеми парами вершин, используя алгоритм Флойда.
Очевидно, что задачу определения расстояния между всеми парами вершин можно решить, используя n раз (поочередно для каждой вершины) один из описанных ранее алгоритмов. Однако оказывается, что n-кратное использование этих алгоритмов не является наилучшим методом. Рассмотрим более эффективный алгоритм для решения поставленной задачи – алгоритм Флойда.
Идея этого алгоритма следующая. Рассмотрим орграф D = (V,X), где V=<v1,…,vn>. Обозначим через dij ( m ) длину кратчайшего из путей из vi в vj с промежуточными вершинами из множества <v1,…,vm>.
Тогда имеем следующие уравнения:
Обоснование второго уравнения достаточно простое. Рассмотрим кратчайший путь из vi в vj с промежуточными вершинами из множества <v1,…, vm,vm+1>. Если этот путь не содержит vm+1 , то dij ( m +1) = dij ( m ) . Если же он содержит vm+1 , то, деля путь на отрезки от vi до vm+1 и от vm+1 до vj , получаем равенство dij ( m +1) = dim ( m ) + dmj ( m ) . Приведенные уравнения дают возможность вычислить расстояния d(vi,vj) = dij ( n ) , где 1 £ i, j £ n.
А л г о р и т м Ф л о й д а
Данные: матрица весов С(D) орграфа D.
Результат: расстояния между всеми парами вершин D[i,j] = d(vi,vj).
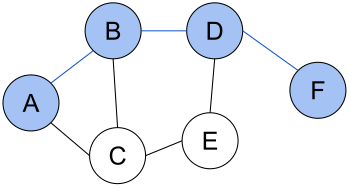
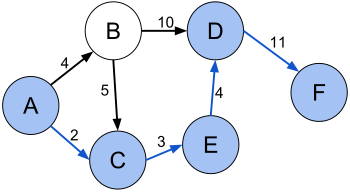
Зада́ча о кратча́йшем пути́ — задача поиска самого короткого пути (цепи) между двумя точками (вершинами) на графе, в которой минимизируется сумма весов рёбер, составляющих путь.
Задача о кратчайшем пути является одной из важнейших классических задач теории графов. Сегодня известно множество алгоритмов для её решения [⇨] .
У данной задачи существуют и другие названия: задача о минимальном пути или, в устаревшем варианте, задача о дилижансе.
Значимость данной задачи определяется её различными практическими применениями
[⇨] . Например, в GPS-навигаторах осуществляется поиск кратчайшего пути между двумя перекрёстками. В качестве вершин выступают перекрёстки, а дороги являются рёбрами, которые лежат между ними. Если сумма длин дорог между перекрёстками минимальна, тогда найденный путь самый короткий.
Содержание
Определение [ править | править код ]
Задача поиска кратчайшего пути на графе может быть определена для неориентированного, ориентированного или смешанного графа. Далее будет рассмотрена постановка задачи в самом простом виде для неориентированного графа. Для смешанного и ориентированного графа дополнительно должны учитываться направления ребер.
Граф представляет собой совокупность непустого множества вершин и рёбер (наборов пар вершин). Две вершины на графе смежны, если они соединяются общим ребром. Путь в неориентированном графе представляет собой последовательность вершин P = ( v 1 , v 2 , … , v n ) ∈ V × V × … × V <displaystyle P=(v_<1>,v_<2>,ldots ,v_








Пусть e i , j <displaystyle e_> 


ightarrow mathbb 







Существуют различные постановки задачи о кратчайшем пути:
- Задача о кратчайшем пути в заданный пункт назначения. Требуется найти кратчайший путь в заданную вершину назначения t, который начинается в каждой из вершин графа (кроме t). Поменяв направление каждого принадлежащего графу ребра, эту задачу можно свести к задаче о единой исходной вершине (в которой осуществляется поиск кратчайшего пути из заданной вершины во все остальные).
- Задача о кратчайшем пути между заданной парой вершин. Требуется найти кратчайший путь из заданной вершины u в заданную вершину v.
- Задача о кратчайшем пути между всеми парами вершин. Требуется найти кратчайший путь из каждой вершины u в каждую вершину v. Эту задачу тоже можно решить с помощью алгоритма, предназначенного для решения задачи об одной исходной вершине, однако обычно она решается быстрее.
В различных постановках задачи, роль длины ребра могут играть не только сами длины, но и время, стоимость, расходы, объём затрачиваемых ресурсов (материальных, финансовых, топливно-энергетических и т. п.) или другие характеристики, связанные с прохождением каждого ребра. Таким образом, задача находит практическое применение в большом количестве областей (информатика, экономика, география и др.).
Задача о кратчайшем пути с учётом дополнительных ограничений [ править | править код ]
Задача о кратчайшем пути очень часто встречается в ситуации, когда необходимо учитывать дополнительные ограничения. Наличие их может значительно повысить сложность задачи [1] . Примеры таких задач:
- Кратчайший путь, проходящий через заданное множество вершин. Можно рассматривать два ограничения: кратчайший путь должен проходить через выделенное множество вершин, и кратчайший путь должен содержать как можно меньше невыделенных вершин. Первое из них хорошо известна в теории исследования операций[2] .
- Минимальное покрытие вершин ориентированного графа путями. Осуществляется поиск минимального по числу путей покрытия графа, а именно подмножества всех s-t путей, таких что, каждая вершина ориентированного графа принадлежит хотя бы одному такому пути [3] .
- Задача о требуемых путях. Требуется найти минимальное по мощности множество s-t путей P = p 1 , … , p m <displaystyle P=<1>,dots ,p_
>> <1>,dots ,t_такое, что для любого t i ∈ R <displaystyle t_in R>
найдется путь p j ∈ P <displaystyle p_
in P> , накрывающий его. R = t 1 , … , t k <displaystyle R=
>> — множество некоторых путей в ориентированном графе G [4] .
- Минимальное покрытие дуг ориентированного графа путями. Задача состоит в отыскании минимального по числу путей подмножества всех путей, такого, что каждая дуга принадлежит хотя бы одному такому пути. При этом возможно дополнительное требование о том, чтобы все пути исходили из одной вершины [5] .
Алгоритмы [ править | править код ]
В связи с тем, что существует множество различных постановок данной задачи, есть наиболее популярные алгоритмы для решения задачи поиска кратчайшего пути на графе:
- Алгоритм Дейкстры находит кратчайший путь от одной из вершин графа до всех остальных. Алгоритм работает только для графов без рёбер отрицательного веса [6] .
- Алгоритм Беллмана — Форда находит кратчайшие пути от одной вершины графа до всех остальных во взвешенном графе. Вес рёбер может быть отрицательным.
- Алгоритм поиска A* находит маршрут с наименьшей стоимостью от одной вершины (начальной) к другой (целевой, конечной), используя алгоритм поиска по первому наилучшему совпадению на графе.
- Алгоритм Флойда — Уоршелла находит кратчайшие пути между всеми вершинами взвешенного ориентированного графа [6] .
- Алгоритм Джонсона находит кратчайшие пути между всеми парами вершин взвешенного ориентированного графа.
- Алгоритм Ли (волновой алгоритм) основан на методе поиска в ширину. Находит путь между вершинами s и t графа (s не совпадает с t), содержащий минимальное количество промежуточных вершин (рёбер). Основное применение — трассировки электрических соединений на кристаллах микросхем и на печатных платах. Также используется для поиска кратчайшего расстояния на карте в стратегических играх.
- Поиск кратчайшего пути на основе алгоритма Килдала [7] .
В работе (Черкасский и др., 1993) [8] представлено ещё несколько алгоритмов для решения этой задачи.
Задача поиска кратчайшего пути из одной вершины во все остальные [ править | править код ]
В такой постановке задачи осуществляется поиск кратчайшего пути из вершины v во все остальные вершины на графе.
Невзвешенный ориентированный граф [ править | править код ]
| Алгоритм | Сложность | Автор |
|---|---|---|
| Поиск в ширину | O(E) |
Ориентированный граф с неотрицательными весами [ править | править код ]
| Алгоритм | Сложность | Автор |
|---|---|---|
| — | O(V 2 EL) | Форд 1956 |
| Алгоритм Беллмана — Форда | O(VE) | Беллман 1958 [9] , Мур 1957 [10] |
| — | O(V 2 log V) | Данциг 1958, Данциг 1960, Minty (cf. Pollack&Wiebenson 1960), Whiting&Hillier 1960 |
| Алгоритм Дейкстры со списком. | O(V 2 ) | Leyzorek et al. 1957 [11] , Дейкстра 1959 [12] |
| Алгоритм Дейкстры с модифицированной двоичной кучей | O((E + V) log V) | — |
| . . . | . . . | . . . |
| Алгоритм Дейкстры с использованием фибоначчиевой кучи | O(E + V log V) | Фридман&Тарьян 1984 [13] , Фридман&Тарьян 1987 [14] |
| — | O(E log log L) | Джонсон 1982, Карлссон&Поблете 1983 |
| Алгоритм Габова | O(E logE/V L) | Габов 1983, Габов 1985 |
| — | O(E + V√log L) | Ахуджа et al. 1990 |
Ориентированный граф с произвольными весами [ править | править код ]
| Алгоритм | Сложность | Автор |
|---|---|---|
| Алгоритм Беллмана — Форда | O(VE) | Беллман [9] , Мур [10] |
Задача о кратчайшем пути между всеми парами вершин [ править | править код ]
Задача о кратчайшем пути между всеми парами вершин для невзвешенного ориентированного графа была поставлена Симбелом в 1953 году [15] , который обнаружил, что она может быть решена за линейное количество манипуляций (умножения) с матрицей. Сложность такого алгоритма O(V 4 ).
Так же для решения данной задачи существуют другие более быстрые алгоритмы, такие как Алгоритм Флойда — Уоршелла со сложностью O(V 3 ), и Алгоритм Джонсона (является комбинацией алгоритмов Бэллмана-Форда и Дейкстры) со сложностью O(VE + V 2 log V).
Применение [ править | править код ]
Задача о поиске кратчайшего пути на графе может быть интерпретирована по-разному и применяться в различных областях. Далее приведены примеры различных применений задачи. Другие применения изучаются в дисциплине, которая занимается исследованием операций [16] .
Картографические сервисы [ править | править код ]
Алгоритмы нахождения кратчайшего пути на графе применяются для нахождения путей между физическими объектами на таких картографических сервисах, как карты Google или OpenStreetMap. В обучающем видео от Google можно узнать различные эффективные алгоритмы, которые применяются в данной сфере [17] .
Недетерминированная машина [ править | править код ]
Если представить недетерминированную абстрактную машину как граф, где вершины описывают состояния, а ребра определяют возможные переходы, тогда алгоритмы поиска кратчайшего пути могут быть применены для поиска оптимальной последовательности решений для достижения главной цели. Например, если вершинами являются состояния Кубика Рубика, а ребром представляет собой одно действие над кубиком, тогда алгоритм может быть применён для поиска решения с минимальным количеством ходов.
Сети дорог [ править | править код ]
Задача поиска кратчайшего пути на графе широко используется при определении наименьшего расстояния в сети дорог.
Сеть дорог можно представить в виде графа с положительными весами. Вершины являются дорожными развязками, а ребра дорогами, которые их соединяют. Веса рёбер могут соответствовать протяжённости данного участка, времени необходимому для его преодоления или стоимости путешествия по нему. Ориентированные ребра можно использовать для представления односторонних улиц. В таком графе можно ввести характеристику, которая указывает на то, что одни дороги важнее других для длительных путешествий (например автомагистрали). Она была формализована в понятии (идее) о магистралях [18] .
Для реализации подхода, где одни дороги важнее других, существует множество алгоритмов. Они решают задачу поиска кратчайшего пути намного быстрее, чем аналогичные на обычных графах. Подобные алгоритмы состоят из двух этапов:
- этап предобработки. Производится предварительная обработка графа без учёта начальной и конечной вершины (может длиться до нескольких дней, если работать с реальными данными). Обычно выполняется один раз и потом используются полученные данные.
- этап запроса. Осуществляется запрос и поиск кратчайшего пути, при этом известны начальная и конечная вершина.
Самый быстрый алгоритм может решить данную задачу на дорогах Европы или Америки за доли микросекунды [19] .
Другие подходы (техники), которые применяются в данной сфере:
Похожие задачи [ править | править код ]
Существуют задачи, которые похожи на задачу поиска кратчайшего пути на графе.
- Поиск кратчайшего пути в вычислительной геометрии (см. евклидов кратчайший путь).
- Задача коммивояжёра. Требуется найти кратчайший маршрут, проходящий через указанные города (вершины) хотя бы по одному разу с последующим возвратом в исходный город. Данная задача относится к классу NP-трудных задач в отличие от задачи поиска кратчайшего пути, которая может быть решена за полиномиальное время в графах без циклов. Задача коммивояжёра решается неэффективно для больших наборов данных.
- Задача канадского путешественника и задача стохастического поиска кратчайшего пути являются обобщением рассматриваемой задачи, в которых обходимый граф заранее полностью неизвестен и изменяется во времени или следующий проход по графу вычисляется на основе вероятностей.
- Задача поиска кратчайшего пути, когда в графе происходят преобразования. Например, изменяется вес ребра или удаляется вершина [20] .
Постановка задачи линейного программирования [ править | править код ]
Пусть дан направленный граф (V, A), где V — множество вершин и A — множество рёбер, с начальной вершиной обхода s, конечной t и весами wij для каждого ребра (i, j) в A. Вес каждого ребра соответствует переменной программы xij.
Тогда задача ставится следующим образом: найти минимум функции F = ∑ i j ∈ A w i j x i j <displaystyle F=sum _w_

Наверняка многим из гейм-девелоперов (или просто людям, увлекающимися програмировагнием) будет интересно услышать эти четыре важнейших алгоритма, решающих задачи о кратчайших путях.
Сформулируем определения и задачу.
Графом будем называть несколько точек (вершин), некоторые пары которых соединены отрезками (рёбрами). Граф связный, если от каждой вершины можно дойти до любой другой по этим отрезкам. Циклом назовём какой-то путь по рёбрам графа, начинающегося и заканчивающегося в одной и той же вершине. И ещё граф называется взвешенным, если каждому ребру соответствует какое-то число (вес). Не может быть двух рёбер, соединяющих одни и те же вершины.
Каждый из алгоритмов будет решать какую-то задачу о кратчайших путях на взвешенном связном. Кратчайший путь из одной вершины в другую — это такой путь по рёбрам, что сумма весов рёбер, по которым мы прошли будет минимальна.
Для ясности приведу пример такой задачи в реальной жизни. Пусть, в стране есть несколько городов и дорог, соединяющих эти города. При этом у каждой дороги есть длина. Вы хотите попасть из одного города в другой, проехав как можно меньший путь.
Считаем, что в графе n вершин и m рёбер.
Пойдём от простого к сложному.
Алгоритм Флойда-Уоршелла
Находит расстояние от каждой вершины до каждой за количество операций порядка n^3. Веса могут быть отрицательными, но у нас не может быть циклов с отрицательной суммой весов рёбер (иначе мы можем ходить по нему сколько душе угодно и каждый раз уменьшать сумму, так не интересно).
В массиве d[0… n — 1][0… n — 1] на i-ой итерации будем хранить ответ на исходную задачу с ограничением на то, что в качестве «пересадочных» в пути мы будем использовать вершины с номером строго меньше i — 1 (вершины нумеруем с нуля). Пусть идёт i-ая итерация, и мы хотим обновить массив до i + 1-ой. Для этого для каждой пары вершин просто попытаемся взять в качестве пересадочной i — 1-ую вершину, и если это улучшает ответ, то так и оставим. Всего сделаем n + 1 итерацию, после её завершения в качестве «пересадочных» мы сможем использовать любую, и массив d будет являться ответом.
n итераций по n итераций по n итераций, итого порядка n^3 операций.
Псевдокод:
Алгоритм Форда-Беллмана
Находит расстояние от одной вершины (дадим ей номер 0) до всех остальных за количество операций порядка n * m. Аналогично предыдущему алгоритму, веса могут быть отрицательными, но у нас не может быть циклов с отрицательной суммой весов рёбер.
Заведём массив d[0… n — 1], в котором на i-ой итерации будем хранить ответ на исходную задачу с ограничением на то, что в путь должно входить строго меньше i рёбер. Если таких путей до вершины j нет, то d[j] = 2000000000 (это должна быть какая-то недостижимая константа, «бесконечность»). В самом начале d заполнен 2000000000. Чтобы обновлять на i-ой итерации массив, надо просто пройти по каждому ребру и попробовать улучшить расстояние до вершин, которые оно соединяет. Кратчайшие пути не содержат циклов, так как все циклы неотрицательны, и мы можем убрать цикл из путя, при этом длина пути не ухудшится (хочется также отметить, что именно так можно найти отрицательные циклы в графе: надо сделать ещё одну итерацию и посмотреть, не улучшилось ли расстояние до какой-нибудь вершины). Поэтому длина кратчайшего пути не больше n — 1, значит, после n-ой итерации d будет ответом на задачу.
n итераций по m итераций, итого порядка n * m операций.
Псевдокод:
Алгоритм Дейкстры
Находит расстояние от одной вершины (дадим ей номер 0) до всех остальных за количество операций порядка n^2. Все веса неотрицательны.
На каждой итерации какие-то вершины будут помечены, а какие-то нет. Заведём два массива: mark[0… n — 1] — True, если вершина помечена, False иначе, d[0… n — 1] — для каждой вершины будет храниться длина кратчайшего пути, проходящего только по помеченным вершинам в качестве «пересадочных». Также поддерживается инвариант того, что для помеченных вершин длина, указанная в d, и есть ответ. Сначала помечена только вершина 0, а g[i] равно x, если 0 и i соединяет ребро весом x, равно 2000000000, если их не соединяет ребро, и равно 0, если i = 0.
На каждой итерации мы находим вершину, с наименьшим значением в d среди непомеченных, пусть это вершина v. Тогда значение d[v] является ответом для v. Докажем. Пусть, кратчайший путь до v из 0 проходит не только по помеченным вершинам в качестве «пересадочных», и при этом он короче d[v]. Возьмём первую встретившуюся непомеченную вершину на этом пути, назовём её u. Длина пройденной части пути (от 0 до u) — d[u]. len >= d[u], где len — длина кратчайшего пути из 0 до v (т. к. отрицательных рёбер нет), но по нашему предположению len меньше d[v]. Значит, d[v] > len >= d[u]. Но тогда v не подходит под своё описание — у неё не наименьшее значение d[v] среди непомеченных. Противоречие.
Теперь смело помечаем вершину v и пересчитываем d. Так делаем, пока все вершины не станут помеченными, и d не станет ответом на задачу.
n итераций по n итераций (на поиск вершины v), итого порядка n^2 операций.
Псевдокод:
