Как доказать неравенство 9 класс

Как доказать неравенство? Рассмотрим некоторые способы доказательства неравенств.

1) Число a больше числа b, если разность a-b — положительное число:

a>b, если a-b>0.

2) Число a меньше числа b, если разность a-b — отрицательное число:

a 0 или a=b (то есть a-b≥0).

4)a≤b, если a-b

Сводится к оценке разности левой и правой частей неравенства и сравнение её с нулём.

1) Доказать неравенство: (a+9)(a-2)

Оценим разность левой и правой частей неравенства:

Оцениваем разность левой и правой частей неравенства:

(3x-5)²≥0 при любом значении переменной x.

Следовательно, (3x-5)²+23>0 при любом x.

Значит, неравенство 9x²+48>30x выполняется при любом действительном значении x.

Что и требовалось доказать.

3) Доказать неравенство: x²+y²+16x-20y+190>0.

(x+8)²≥0 при любом значении x,

(y-10)²≥0 при любом значении y,

Следовательно, (x+8)²+(y-10)²+26>0 при любых действительных значениях переменных x и y.

А это значит, что x²+y²+16x-20y+190>0.

Что и требовалось доказать.

II. Доказательство неравенств методом «от противного».

Высказываем предположение, что доказываемое неравенство неверно, и приходим к противоречию.

Предположим, что неравенство, которое нам нужно доказать, неверно. Тогда

Раскрываем скобки и упрощаем:

Поскольку (a₁b₂-a₁b₁)²≥0 при любых действительных значениях переменных, то -(a₁b₂-a₁b₁)²≤0. Пришли к противоречию. Значит, наше предположение было неверно. Следовательно,

Что и требовалось доказать.

III. Доказательство неравенств с помощью геометрической интерпретации.

Таким способом, например, можно доказать неравенство о среднем арифметическом и среднем геометрическом (частный случай неравенства Коши).

IV. Доказательство неравенств с использованием очевидных неравенств.

Доказать неравенство: a²+b²+c²≥ab+bc+ac.

Так при любых действительных значениях переменных (a-b)²≥0, (b-c)²≥0 и (a-c)²≥0, то очевидно, что (a-b)²+(b-c)²+(a-c)²≥0.

Раскрываем скобки по формуле квадрата разности и упрощаем:

Осталось перенести три слагаемые в правую часть:

Что и требовалось доказать.

V. Доказательство неравенств с помощью ранее доказанных неравенств.

Основные неравенства, на которые опираются при доказательстве других неравенств:

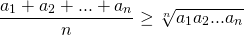
При a₁= a₂= …= a_n неравенство превращается в равенство.

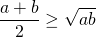
• Сумма положительных взаимно-обратных чисел не меньше двух:

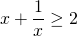
Применяется также аналог неравенства для отрицательных взаимно-обратных чисел:

при x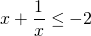

Равенство достигается лишь в случае, когда числа x_i и y_i пропорциональны, то есть существует число k такое, что для любого i=1,2,…,n выполняется равенство x_i=ky_i.

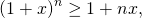
где x>-1, n — натуральное число.

Равенство достигается лишь при x=0 и n=1.

• Обобщённое неравенство Бернулли

Если x>-1, n — действительное число:

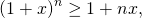
При 0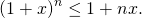

В обоих случаях равенство возможно лишь при x=0.

Модуль суммы не превосходит суммы модулей

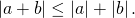
Равенство достигается, если a и b имеют одинаковые знаки (a≥0 и b≤0 либо a≤0, b≤0).

• Модуль разности больше либо равен модуля разности модулей

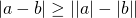
1) Доказать неравенство при x>0, a>0, b>0, c>0:

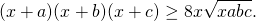
Используем неравенство Коши о среднем арифметическом и среднем геометрическом

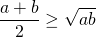
для каждого из множителей:

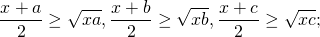
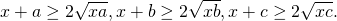
Так как по условию x>0, a>0, b>0, c>0, то x+a>0, x+b>0, x+c>0 и

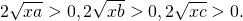0,2sqrt > 0,2sqrt > 0. ]" title="Rendered by QuickLaTeX.com"/>

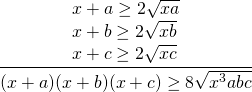
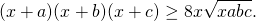
Что и требовалось доказать.

2) Доказать неравенство:

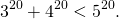
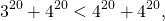
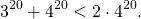
Таким образом, для доказательства нашего неравенства надо показать, что

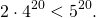
разделим обе части неравенства на 4 в двадцатой степени (при делении на положительное число знак неравенства не изменяется):

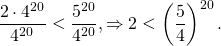
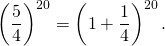
Применим неравенство Бернулли:

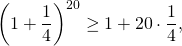
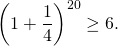
Так как в неравенстве

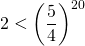
правая часть больше либо равна 6, это равенство верно. Следовательно,

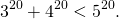
Что и требовалось доказать.

Помимо перечисленных, существуют другие способы доказательства неравенств (метод математической индукции и т.д.).

Умение доказывать неравенства применяется во многих разделах алгебры (например, метод оценки решения уравнений сводится к доказательству неравенств).

Пусть теперь нашлись такие неотрицательные числа А, В и С, для которых выполняется неравенство

, что невозможно ни при каких действительных А,В и С. Сделанное выше предположение опровергнуто, что доказывает исследуемое исходное неравенство.

Просмотр содержимого документа
«Приемы доказательства неравенств, содержащих переменные 9 класс »

Приемы доказательства неравенств, содержащих переменные

Если вы хотите участвовать в большой жизни, то наполняйте свою голову математикой, пока есть к тому возможность. Она окажет вам потом огромную помощь во всей вашей работе. (М.И. Калинин)

• Представление левой части неравенства в виде суммы неотрицательных слагаемых (правая часть равна 0) с использованием тождеств.

Пример 1 . Доказать что для любого х ϵ R

для квадратичной функции

что означает её положительность при любом действительном х .

Пример 2 . Доказать, что для любых x и y

Пример 3 . Доказать, что

Пример 4 . Доказать, что для любых a и b

для любых действительных х и у

2. Метод от противного

Вот хороший пример применения данного метода.

Но ,что явно доказывает, что наше предположение неверно.

Пример 5 . Доказать, что для любых чисел А,В,С справедливо неравенство

Доказательство. Очевидно, что данное неравенство достаточно установить для неотрицательных А, В и С, так как будем иметь следующее отношения:

, что является обоснованием исходного неравенства .

Пусть теперь нашлись такие неотрицательные числа А, В и С , для которых выполняется неравенство

, что невозможно ни при каких действительных А,В и С . Сделанное выше предположение опровергнуто, что доказывает исследуемое исходное неравенство.

0 = для х ϵ R для х ϵ R" w

Использование свойств квадратного трехчлена

Метод основан на свойстве неотрицательности квадратного трехчлена , если

Пример 6 . Доказать, что

0, D D= = P(x)0 и верно при любых действительных значениях х и у. для х ϵ R" w

Пример 7 . Доказать, что для любых действительных х и у имеет место быть неравенство

Доказательство. Рассмотрим левую часть неравенство как квадратный трехчлен относительно х:

верно при любых действительных значениях х и у.

Пример 8 . Доказать, что

для любых действительных значениях х и у.

Это означает, что для любых действительных у и неравенство

выполняется при любых действительных х и у.

Метод введения новых переменных или метод подстановки

Пример 9 . Доказать, что для любых неотрицательных чисел х, у, z

Доказательство. Воспользуемся верным неравенством для , ,

Получаем исследуемое неравенство

( )* ( ) 0 , что доказывает неравенство для а ϵ R" w

Использование свойств функций.

Пример 10 . Докажем неравенство

Доказательство. Рассмотрим 2 случая:

причем равенство достигается только при а= b=0.

( )* ( ) 0 , что доказывает неравенство

" w

Пример 11 . Докажем, что для любых

Если , то знаки чисел и совпадают, что означает положительность исследуемой разности =

1)" w

Применение метода математической индукции

Данный метод применяется для доказательства неравенств относительно натуральных чисел.

• Проверим истинность утверждения при

2) Предположим верность утверждения при

3) Докажем истинность утверждения при n=k+1.

Вывод: утверждение верно для любого n ϵ N .

Использование замечательных неравенств

• Теорема о средних (неравенство Коши)
• Неравенство Коши – Буняковского
• Неравенство Бернулли

Рассмотрим каждое из перечисленных неравенств в отдельности.

Применение теоремы о средних (неравенства Коши)

Среднее арифметическое нескольких неотрицательных чисел больше или равно их среднего геометрического

Знак равенства достигается тогда и только тогда, когда

Рассмотрим частные случаи этой теоремы:

0, тогда Пусть n=3, , , , тогда" w

• Пусть n=2 , , , тогда
• Пусть n=2, a0, тогда
• Пусть n=3, , , , тогда

Пример 13 . Доказать, что для всех неотрицательных a,b,c выполняется неравенство

Неравенство Коши — Буняковского

Неравенство Коши — Буняковского утверждает, что для любых ; справедливо соотношение

Доказанное неравенство имеет геометрическую интерпретацию. Для n=2,3 оно выражает известный факт, что скалярное произведение двух векторов на плоскости и в пространстве не превосходит произведение их длин. Для n=2 неравенство имеет вид: . Для n=3 получим

Пример 14. Доказать, что для любых a,b,c ϵ R справедливо неравенство

Доказательство. Запишем исследуемое неравенство в следующем виде:

Это заведомо истинное неравенство, так как является частным случаем неравенства Коши – Буняковского.

Пример 15. Доказать, что для любых a,b,c ϵ R справедливо неравенство

Доказательство. Достаточно записать данное неравенство в виде

и сослаться на неравенство Коши – Буняковского.

-1, то для всех натуральных значений n выполняется неравенство Неравенство может применяться для выражений вида Кроме того, очень большая группа неравенств может быть легко доказана с помощью теоремы Бернулли." w

Неравенство Бернулли утверждает, что если х -1, то для всех натуральных значений n выполняется неравенство

Неравенство может применяться для выражений вида

Кроме того, очень большая группа неравенств может быть легко доказана с помощью теоремы Бернулли.

Доказательство. Положив х =0,5 и применив теорему Бернулли для выражения

, получим требуемое неравенство.

по теореме Бернулли, что и требовалось.

Давида Гильберта спросили об одном из его бывших учеников. "А, такой-то? — вспомнил Гильберт. — Он стал поэтом. Для математики у него было слишком мало воображения.

Идёт приём заявок

Подать заявку

Для учеников 1-11 классов и дошкольников

Дата _______ Урок № Сынып/ Класс 9

Тақырыбы: Доказательство неравенств

расширить, обобщить и систематизировать знания о неравенствах;

закрепить знания свойств неравенств;

способствовать выработке навыков и умений в доказательстве неравенств.

Тип урока: урок открытия новых знаний.

Формы работы на уроке: индивидуальная, коллективная; устная, письменная.

карточки – задания для индивидуальной работы, мультимедийный проектор.

2. II. этап. Устно- письменный опрос учащихся с целью установления содержательных связей между ведущими линиями школьного курса математики.

1. Какие из следующих чисел: –2; –1; 0; 2; 3 – являются решением неравенства х 3 – 2х ≥ 1?

2. Подберите два каких-нибудь числа разных знаков, чтобы их сумма была больше 5.

Контроль усвоения материала(самостоятельная работа).

III. Объяснение нового материала.

В математике неравенство есть утверждение об относительной величине или порядке двух объектов, или о том, что они просто не одинаковы.

Доказать – значит привести аргументы, которые отметут все сомнения в правоте высказанного. Для доказательство неравенств часто используют один простой факт:

Говорят, что действительное число a больше (меньше) действительного числа b , если их разность a − b является положительным (отрицательным) числом.
Основные свойства неравенств

Некоторые опорные неравенства, которые часто используются для доказательства других неравенств:

в частности, для натурального n ≥2, a 2> b 2 то na √> nb √;

Существует несколько методов доказательства неравенств. Мы рассмотрим их на примере неравенства:

где a – положительное число.

1). Использование известного или ранее доказанного неравенств а.

Известно, что ( a – 1 )² 0 .

2). Оценка знака разности между частями неравенства . Рассмотрим разность между левой и правой частью:

более того, равенство имеет место только при a = 1 .

3). Доказательство от противного.

Умножая обе части неравенства на a , получим: a 2 + 1 a , т.e. a 2 + 1 – 2 a или ( a – 1 ) 2 что неверно. ( Почему ? ) . Полученное противоречие доказывает справедливость рассматри

4). Метод неопределённого неравенства.

Неравенство называется неопределённым , если у него знак / или / , т.е. когда мы не знаем в какую сторону следует повернуть этот знак, чтобы получить справедливое неравенство. Здесь действуют те же правила, что и с обычными неравенствами.

Рассмотрим неопределённое неравенство:

Умножая обе части неравенства на a , получим: a 2 + 1 / 2 a , т.e. а 2 + 1 – 2 a / 0 , или ( a – 1 ) 2 / 0 , но здесь мы уже знаем, как повернуть

знак / , чтобы получить верное неравенство ( Как? ). Поворачивая его

в нужном направлении по всей цепочке неравенств снизу вверх, мы
получим требуемое неравенство.

Докажем, что (a+b)(ab+1) 4ab, при а0, b0.

Доказательство: Рассмотрим a+b и ab+1.

Используем очевидное неравенство Коши:

И для второго множителя.

Перемножим получившиеся неравенства:

IV. Формирование умений и навыков.

. Для самостоятельного решения

Доказательство неравенств

Образец 1. Докажи самостоятельно:

рассмотрим разность: 1) (a+6) 2 >12a;

a 2 +4 > 0 для любого a, значит 3) b(b — 4) > — 4.

a(a — 6) 2 Докажи самостоятельно:

рассмотрим разность: 1) x(x+10) 2 ;

V. 4 этап . Оценочно -рефлексивный .

Подведение итогов урока, комментарии по домашнему заданию. Обратить внимание учащихся на теоретические факты, которые вспомнили на уроке, о необходимости их выучить.