Энергия поля сферы поверхность которой заряжена

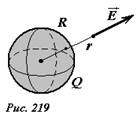
Пусть электрический заряд Q равномерно распределен по поверхности сферы радиуса R. Вне сферы электрическое поле, создаваемое зарядами на сфере, эквивалентно полю точечного заряда, помещенного в центре сфере (рис. 219). Внутри сферы поле отсутствует. Так напряженность поля в точке, находящейся на расстоянии r от центра сферы равна

в частности непосредственно у поверхности сферы напряженность поля равна

Обратим внимание, что произведение S=4πR2 есть площадь сферы, поэтому отношение Q4πε0=σ является поверхностной плотностью заряда на сфере, поэтому напряженность поля у поверхности сферы выражается той же формулой, что и напряженность поля между пластинами, рассмотренными в предыдущем разделе E0=σε0. Потенциал поверхности сферы также был вычислен нами ранее

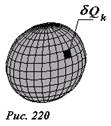
Рассчитаем теперь энергию поля, создаваемого зарядами на сфере. Мысленно разделим заряд сферы на N равных малых частей (рис.220), величины которых равны δQk=QN (k = 1,2…N). Рассмотрим один из этих малых зарядов. В точке его расположения потенциал поля, создаваемого всеми остальными (N-1) зарядами равен φk=(N−1)δQ4πεR. С использованием симметричной формулы U=12∑kqkφk , выражение для энергии взаимодействия приобретает вид

данная сумма содержит N одинаковых слагаемых, поэтому равна

Так как число частей N, на которые разбивается сфера, может быть сделано сколь угодно большим, поэтому в пределе N→∞ слагаемое 1N исчезает, поэтому окончательное выражение для энергии взаимодействия зарядов сферы имеет вид

Заметим, что полученное выражение имеет вид U=12Qφ0. Если сразу заявить, что уменьшение заряда на малую величину δQ пренебрежимо мало изменяет потенциал сферы, то результат (4) получается прямым применением формулы для энергии взаимодействия зарядов. Однако обращение с малыми величинами требует известной строгости, поэтому мы и привели несколько «удлиненный» вывод.

Приведем еще один вывод этой же формулы. Для этого энергию системы рассчитаем как работу, которую необходимо совершить, чтобы зарядить сферу. Мысленно будем заряжать сферу малыми равными порциями заряда δQk=QN (k = 1,2…N), которые будем переносить на сферу из «бесконечности». Если сфера не заряжена, то перенесение первой «порции» заряда не требует совершения никакой работы. После того как сфера приобрела некоторый электрический заряд, перенесение следующей порции заряда требует совершения работы по преодолению сил отталкивания со стороны зарядов сферы. Если на сферу перенесено (k-1) порций заряда, то ее потенциал равен φ(k−1)=(k−1)δQ4πεR . Поэтому для того, что бы перенести на сферу следующую порцию заряда необходимо совершить работу

Заметьте, что для перенесения каждой следующей порции заряда надо совершать большую работу.

Полная работа по зарядке сферы (равная энергии электрического поля сферы) выражается суммой геометрической прогрессии

Как и следовало ожидать, мы получили выражение, полностью совпадающее с (13), при бесконечном уменьшении порций переносимых зарядов ( N→∞) мы опять приходим к формуле (14).

В этом нет ничего удивительного, так как в первом случае мы подсчитали энергию, которая выделится при разбегании зарядов со сферы, а во втором – энергию, которую необходимо затратить, чтобы собрать их обратно.

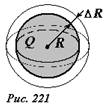
Покажем, что энергию взаимодействия зарядов и в этом случае можно истолковать как энергию электрического поля, «размазанную» по всему пространству, где существует поле. Представим, что радиус сферы увеличился на малую величину ΔR, а ее заряд при этом не изменился. Согласно формуле (14) энергия взаимодействия зарядов при этом уменьшится. В пространстве вне сферы увеличенного радиуса электрическое поле не изменилось, а в тонком сферическом слое между начальной и расширенной сферами – исчезло (рис. 221). Поэтому следует считать, что уменьшение энергии взаимодействия зарядов при увеличении радиуса сферы равно энергии, которая заключена в этом тонком сферическом слое. При малой толщине слоя его объем можно вычислить как произведение площади сферы на толщину слоя ΔV=4πR2ΔR . Пренебрегая изменением напряженности поля в пределах тонкого слоя, энергию, заключенную в нем запишем в виде

где w — плотность энергии поля. С другой стороны эта энергия равна изменению энергии взаимодействия зарядов при увеличении радиуса сферы

На последнем шаге, мы пренебрегли малым изменением радиуса ΔR. Наконец, выразим заряд шара через напряженность электрического поля у его поверхности Q=4πεR2E :

Из сравнения с формулой (16) следует, что и в рассматриваемом случае плотность энергии электрического поля выражается формулой w=εE22.

Найдем напряженность и потенциал электрического поля, создаваемого зарядом Q, равномерно распределенным по поверхности сферы. Так как заряд распределен сферически симметрично, создаваемое им поле также будет сферически симметричным. Построим декартову систему координат так, чтобы ее начало совпало с центром О сферы (рис. 1.15).

где Е(г) — проекция вектора Е на радиус-вектор г. Согласно этой формуле вектор напряженности электрического поля в любой точке Р(г) коллинеарен радиус-вектору г, а его модуль зависит только от расстояния г до центра О. Из формулы (1.64) следует также, что силовые линии поля есть прямые, проходящие через начало координат. При этом эквипотенциальные поверхности являются сферами с центром в начале координат, а зависимость потенциала от координат точки Р будет сферически симметричной функцией вида

Рис. 1.15. К вычислению напряженности пом заряженной сферы

т.е. потенциал будет зависеть только от модуля г радиус-вектора. Подстановка этой функции в формулу (1.22) приводит к выражению (1.64), в котором

Формула (1.64) определяет направление вектора Е . Проекцию Е(г) этого вектора на радиальное направление можно найти при помощи теоремы Гаусса. Для этого следует вычислить

поток Фе вектора Е через поверхность S сферы произвольного радиуса г, центр которой совпадает с центром О заряженной сферы. При этом радиус г может как меньше радиуса Я заряженной сферы, так и больше его (рис. 1.15).

Векторный элемент поверхности сферы описывается выражением (1.58). Подстановка этого выражения и выражения (1.64) в формулу (1.56) приводит к следующему результату:

В такой системе координат сферически симметричное векторное поле Е = Е (г) описывается формулой

Применим теорему Гаусса. Если радиус г сферы S меньше радиуса Я заряженной сферы, то заряд внутри сферы 5 будет равен нулю. Если же радиус г сферы 5 больше радиуса Я, то вся заряженная сфера окажется внутри сферы S. Таким образом, теорема Гаусса (1.61) приводит к равенству

этого равенства вытекает зависимость

График этой зависимости для случая, когда Q > 0, показан на рис. 1.16.

Рис. 1.16. Зависимость напряженности поля от расстояния г

Рис. 1.17. Зависимость потенциала от расстояния г

Нетрудно проверить, что непрерывная функция р = у?(г), подстановка которой в формулу (1.65) приводит к найденной зависимости Е = Е(г), такова

График функции (1.67) изображен на рис. 1.17.

Полученные зависимости позволяют утверждать, что электрическое поле внутри равномерно по поверхности заряженной сферы отсутствует, а вне этой сферы электрическое поле такое же, как поле точечного заряда.

Наука — есть лучший современный способ удовлетворения любопытства за счет государства. (Л.А. Арцимович)

1. Энергия системы точечных зарядов.

Пусть имеются два неподвижных точечных заряда (рис.16.1). Поле — электростатическое и потенциальное, силы консервативны. Работа, которую совершает поле заряда q₁ при переносе заряда q₂ из бесконечности в точку 2 в соответствии с (6.3) и (6.16) равна

(16.2)

Это энергия взаимодействия двух точечных зарядов, которая в зависимости от знака зарядов, может быть как положительной, так и отрицательной. Можно говорить, что заряд q₂ в поле, созданном зарядом q₁ обладает потенциальной энергией W_p. Из симметрии формулы ясно, что можно рассуждать и наоборот.

Теперь добавим в систему третий заряд q₃ (рис.16.2). По аналогии

а энергия всей системы зарядов

Заметим, что в это выражение все величины входят симметрично, т.е. безразлично, в какой последовательности мы собирали систему. Эта энергия не зависит от процесса, а лишь от состояния системы. Потенциальная энергия — это функция состояния системы. Нулевое значение берется при бесконечном удалении зарядов друг от друга. Заметим также, что это энергия всей системы, энергия взаимодействия, поэтому бессмысленно говорить, что какая-то часть этой энергии принадлежит одному из зарядов. Здесь мы не учитываем собственную энергию каждого точечного заряда.

Это та энергия, которую нужно затратить, чтобы собрать из бесконечно малых порций заряда точечный заряд. Формально она бесконечна, так как необходимо уложить заряды в нулевой объем. Кроме того, эту энергию изменить весьма проблематично. Поэтому можно считать, что это постоянная величина. А мы помним, что потенциальную энергию определяют с точностью до постоянной, которую всегда можно отбросить, так как смысл имеет не сама энергия, а ее изменение.

Обобщив сказанное, можно записать потенциальную энергию взаимодействия системы из N точечных зарядов

(16.5)

Множитель 1/2 появляется в связи с тем, что при суммировании каждая пара зарядов входит в формулу два раза. Перепишем это выражение несколько по иному

, N>1 (16.6)

где j _i — потенциал в точке, где находится заряд q_i, созданный всеми другими зарядами.

Напомним, что энергия одного точечного заряда в поле, созданном всеми другими зарядами (рис.16.2) вычисляется в соответствии с формулами (6.16)-(6.18) как

(16.7)

2. Энергия заряженного тела.

Если распределение зарядов в пространстве непрерывное, то

(16.8)

Эту формулу уже можно трактовать и по-другому. При конечных размерах тела потенциал в любой точке пространства конечен в отличии от точечного заряда. Поэтому эту формулу можно рассматривать и как учитывающую собственную энергию заряда, то есть энергию, которую нужно было затратить, чтобы собрать этот заряд из бесконечно малых частей.

Заметим, что полная энергия (16.8) всегда положительна. При переходе к точечным зарядам она становится бесконечной положительной величиной. Если от этой бесконечной величины отнять бесконечную собственную энергию точечных зарядов, то останется конечная энергия взаимодействия точечных зарядов друг с другом (16.6), которая может быть как положительной, так и отрицательной.

Формула (16.7) соответствует духу теории дальнодействия, так как выражает энергию через потенциалы и заряды тел.

3. Энергия заряженной сферы.

Для примера рассчитаем энергию сферы с зарядом Q и радиусом R. Сначала запишем ее объемную плотность заряда как r =A d (r-R), где d — дельта-функция Дирака, а константу А найдем из очевидного соотношения

где dV=4 p r 2 dr. Очевидно, что — то есть поверхностная плотность заряда. Потенциал, который создает сфера, нам известен (7.17). Тогда энергия сферы в соответствии с (16.8)

(16.24)

Хотя потенциал сферы внутри и снаружи описывается разными формулами, но при вычислении необходимо только его значение на поверхности сферы, а там он одинаков.

4. Энергия конденсатора.

Известно, что если взять заряженный конденсатор и замкнуть его обкладки через сопротивление, то по цепи потечет ток, проводник нагреется, выделится какое-то количество теплоты. Следовательно, заряженный конденсатор обладал запасом энергии.

Перекидывая ключ на схеме (рис.16.3)(попробуйте это сделать движением мыши), можно периодически заряжать конденсатор от источника и разряжать его через резистор. Лампочка при этом будет на короткое время вспыхивать. Найдем выражение для энергии плоского конденсатора, используя (16.6). Нас очень выручит то, что поле между обкладками этого конденсатора однородно. Тогда

Оказывается, что это выражение справедливо для любого конденсатора. Кроме того, учтем, что часто используют понятие напряжения U, как модуля разности (или изменения) потенциалов. В электростатике это справедливо. Более подробно мы разберем понятие напряжения в лекции №18.

Учитывая вышесказанное и (15.3), энергию конденсатора можно записать как

(16.26)

Все три формы записи эквивалентны и применяются при решении задач в зависимости от того, какая из величин остается постоянной.

5. Энергия электрического поля.

Мы выяснили, что система точечных зарядов и конденсатор обладают энергией. Можно предположить, что это энергия самих зарядов, в том числе и расположенных на обкладках конденсатора. Однако можно говорить, что это энергия электрического поля, созданного системой зарядов или поля внутри конденсатора. Какая из этих точек зрения более правильная неясно. Ответ может дать только опыт, а в электростатике такой эксперимент невозможен, так как нет поля без зарядов, и зарядов без поля. Поэтому этот волнующий вопрос мы оставим без внимания до тех пор, пока не начнем изучать переменные поля.

Здесь выразим энергию конденсатора через характеристики поля, зная формулу емкости плоского конденсатора (15.6), связь между напряженностью и потенциалом (7.8), и очевидное выражение для объема V=Sd

Таким образом, энергия равна

(16.28)

Естественно, это справедливо, если нет сторонних потерь и диэлектрическая проницаемость постоянна. Однако нетрудно догадаться, как выглядит это выражение в произвольном случае для бесконечно малого объема.

(16.30)

Часто говорят об энергии единицы объема или о плотности энергии электростатического поля

(16.31)

Формула (16.30) соответствует духу теории близкодействия, так как выражает энергию через характеристики поля. Сравните с (16.8). Эти формулы эквивалентны.

rem: Если вы считаете, что усвоили данный материал, то попробуйте поразмышлять о следующем. Энергия конденсатора и поля в нем согласно (16.26) и (16.30) положительна, а энергия разноименно заряженных пластин по (16.5) отрицательна. Как вы объясните это противоречие?

6. Энергия заряженной сферы(еще раз).

Вновь вернемся к задаче о заряженной сфере. Добавим вокруг нее среду с диэлектрической проницаемостью e . Рассчитаем еще двумя способами ее энергию. Емкость ее известна (15.10), тогда по (16.26)

(16.32)

Теперь рассчитаем энергию поля, созданного этой сферой, не забыв о том, что внутри поля нет.

(16.33)

Как и ожидалось, результаты (16.24), (16.32) и (16.33) совпадают.

rem: Заметим, что потенциальная энергия подчиняется принципу минимума: в любой системе проводников при фиксированных значениях потенциалов заряд распределяется таким образом, чтобы энергия, запасенная во всем поле была минимальна.

7. Сила взаимодействия пластин конденсатора.

Ранее отмечалось, что для любого потенциального поля выполняется следующее соотношение между силой и энергией

(16.34)

Тогда несложно рассчитать силу взаимодействия между пластинами плоского конденсатора.

Через характеристики поля:

, (16.38)

Следовательно, сила, приходящаяся на единицу площади пластин конденсатора, численно равна плотности энергии. Как и следовало ожидать это сила притяжения, так как пластины заряжены разноименно.

Через энергию конденсатора (16.26) расчет еще проще

Эта формула в точности совпадает с (12.10).

Заметим, что сила стремится уменьшить область пространства, заполненного электрическим полем, то есть уменьшить потенциальную энергию в соответствии с принципом минимума потенциальной энергии.

8. Классический радиус электрона.

Будем считать, что электрон — это маленький шарик с зарядом q=е, радиусом R и диэлектрической проницаемостью e ₁. Вокруг него среда с диэлектрической проницаемостью e ₂.

Снаружи шара все аналогично заряженной сфере, так как поля шара и сферы снаружи одинаковы. Тогда энергия поля снаружи равна

Внутри равномерно заряженного шара поле тоже известно (5.14), поэтому

Интеграл несложный. Мы легко получаем энергию поля внутри шара

Очевидно, что полная энергия заряженного шара

Согласно знаменитому соотношению Эйнштейна между массой и энергией

где m— масса электрона, с— скорость света в вакууме. Приравнивая, получаем

(16.45)

На коэффициент в скобках не обращают внимания, так как непонятно, что такое диэлектрическая проницаемость среды внутри электрона. Ясно, что эта величина находится в диапазоне от 0,5 до 0,6, поэтому ее для оценки считают равной единице, и определяют классический радиус электрона по формуле

(16.46)

Расчет показывает, что эта величина равна

Вспомним, что радиус самого маленького атома водорода — первый боровский радиус R_b=0,529 × 10 -10 м , и убедимся, что атом в, основном, пуст, и напоминает солнечную систему в миниатюре.

9. Точечный заряд и бесконечная плоскость.

Вычислим энергию, которой обладает точечный заряд вблизи заземленной проводящей плоскости (см. лк.№10 п.1). Сила, действующая на заряд известна. Вычислим работу, совершаемую этой силой, при перемещении заряда в бесконечность. При бесконечном расстоянии энергия — 0.

(16.48)

теперь найдем ту же самую величину как энергию взаимодействия двух точечных зарядов: самого заряда и его зеркального отображения по формуле (16.2).

Результат получился в 2 раза больше?! Дело в том, что за плоскостью на самом деле поля нет, поэтому от полученного выражения нужно оставить только половину, что как раз и совпадает с (16.48).

10. Конденсатор с частичным заполнением-1.

В качестве дополнительной тренировки рассчитаем силу, действующую на единице поверхности диэлектрика, если заряженный конденсатор заполнен им не полностью, а частично. Конденсатор отключен от источника питания.

Сначала рассмотрим следующую конфигурацию (рис.16.6). Данный конденсатор можно рассматривать как два конденсатора, соединенных последовательно. Тогда их емкости соответственно

и , а общая емкость

Тогда в соответствии с (16.34)

(16.54)

Если e ₁ e ₂, то F_x e ₁> e ₂, то F_x>0. Очевидно, что диэлектрик втягивается в область с меньшей диэлектрической проницаемостью. Направление силы легко было определить, как силу, действующую со стороны поля на поляризационный заряд. И, наконец, если конденсатор заполнится полностью диэлектриком с большей диэлектрической проницаемостью, то его энергия станет меньше в соответствии с принципом минимума.

Выразим формулу (16.54) через характеристики поля, учитывая, что Q= s S=DS. Заметим, что индукции по обе стороны от границы одинаковы. Тогда

Следовательно, сила, приходящаяся на единицу площади пластин конденсатора, численно равна разности плотности энергий

(16.57)

Сравните с (16.38) и вспомните, что снаружи конденсатора поля нет. Заметим только, что (16.38) — это сила, действующая на заряженную пластину (обкладку), а (16.57) — сила, действующая на поверхность диэлектрика. Они отличаются знаками, но по модулю равны, ведь третий закон Ньютона должен выполняться и здесь.

Эту же формулу можно получить быстрее, используя (16.30) и (16.31).

где V₁=Sx, V₂=S(d-x) — объемы областей, заполненных каждым диэлектриком. При смещении границы плотности энергии не меняются. После дифференцирования вновь получаем формулу (16.57).

11. Конденсатор с частичным заполнением-2.

Пусть теперь диэлектрик заполняет конденсатор по-другому (рис.16.7). Сторона пластины равна а. Очевидно, что такую систему можно рассмотреть как два параллельно соединенных конденсатора. Далее все делаем по аналогии с п.10 и получаем следующее выражение для силы

(16.59)

Опять видим, что сила направлена в сторону диэлектрика с меньшей диэлектрической проницаемостью. Учтем, что при этом распределение зарядов на пластинах конденсатора меняется. Однако напряженности поля справа и слева от границы равны.

Через характеристики поля сила, действующая на единицу поверхности, выражается следующим образом

(16.60)

Формулы (16.57) и (16.60) очень похожи.

Можно сделать общий вывод:

Lex: Сила, действующая на границу диэлектрика, пропорциональна разности плотностей энергии электростатического поля и направлена в сторону диэлектрика с меньшей диэлектрической проницаемостью.

Теперь мы легко можем рассчитать, на какую высоту поднимется жидкий диэлектрик между двумя заряженными пластинами (лк. №12 п.7 рис.12.11). Остановит подъем гидростатическое давление. Сверху над диэлектриком — вакуум. Тогда

отсюда высота подъема

Попробуйте решить ту же задачу, если конденсатор подключен к источнику питания. Результат должен быть аналогичен (16.60). Если ошибетесь со знаком, то посмотрите разъяснения Фейнмана (т.5 стр 158 и 213).