Функция частота в excel примеры

Функция ЧАСТОТА( ) , английская версия FREQUENCY(), вычисляет частоту попадания значений в заданные пользователем интервалы и возвращает соответствующий массив чисел.

Функцией ЧАСТОТА() можно воспользоваться, например, для подсчета количества результатов тестирования, попадающих в определенные интервалы (См. Файл примера )

Синтаксис функции

ЧАСТОТА(массив_данных;массив_интервалов)

Массив_данных — массив или ссылка на множество ЧИСЛОвых данных, для которых вычисляются частоты.

Массив_интервалов — массив или ссылка на множество интервалов, в которые группируются значения аргумента «массив_данных».

Функция ЧАСТОТА() вводится как формула массива после выделения диапазона смежных ячеек, в которые требуется вернуть полученный массив распределения (частот). Т.е. после ввода формулы необходимо вместо нажатия клавиши ENTER нажать сочетание клавиш CTRL+SHIFT+ENTER.

Количество элементов в возвращаемом массиве на единицу больше числа элементов в массиве «массив_интервалов». Дополнительный элемент в возвращаемом массиве содержит количество значений, превышающих верхнюю границу интервала, содержащего наибольшие значения (см. пример ниже).

Пример

Пусть в диапазоне А2:А101 имеется исходный массив чисел от 1 до 100.

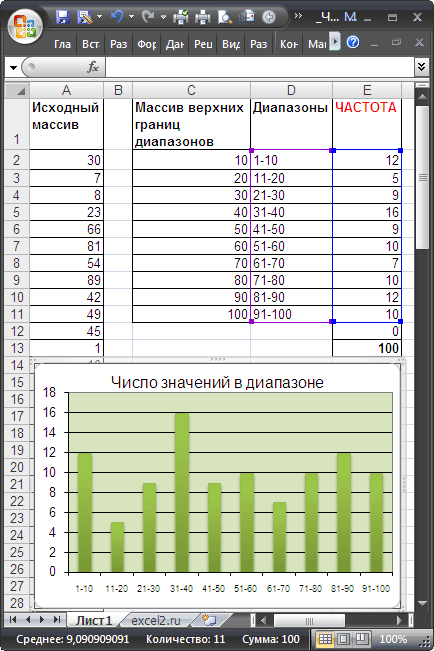
Подсчитаем количество чисел, попадающих в интервалы 1-10; 11-20; . 91-100.

Сформируем столбце С массив верхних границ диапазонов (интервалов). Для наглядности в столбце D сформируем текстовые значения соответствующие границам интервалов (1-10; 11-20; . 91-100).

Для ввода формулы выделим диапазон Е2:Е12, состоящий из 11 ячеек (на 1 больше, чем число верхних границ интервалов). В Строке формул введем =ЧАСТОТА($A$2:$A$101;$C$2:$C$11) . После ввода формулы необходимо нажать сочетание клавиш CTRL+SHIFT+ENTER. Диапазон Е2:Е12 заполнится значениями:

• в Е2 — будет содержаться количество значений из А2:А101, которые меньше или равны 10;
• в Е3 — количество значений из А2:А101, которые меньше или равны 20, но больше 10;
• в Е11 — количество значений из А2:А101, которые меньше или равны 100, но больше 90;
• в Е12 — количество значений из А2:А101, которые больше 100 (таких нет, т.к. исходный массив содержит числа от 1 до 100).

Примечание. Функцию ЧАСТОТА() можно заменить формулой = СУММПРОИЗВ(($A$5:$A$104>C5)*($A$5:$A$104 (См. Файл примера )

При анализе данных периодически возникает задача подсчитать количество значений, попадающих в заданные интервалы "от и до" (в статистике их называют "карманы"). Например, подсчитать количество звонков определенной длительности при разборе статистики по мобильной связи, чтобы понимать какой тариф для нас выгоднее:

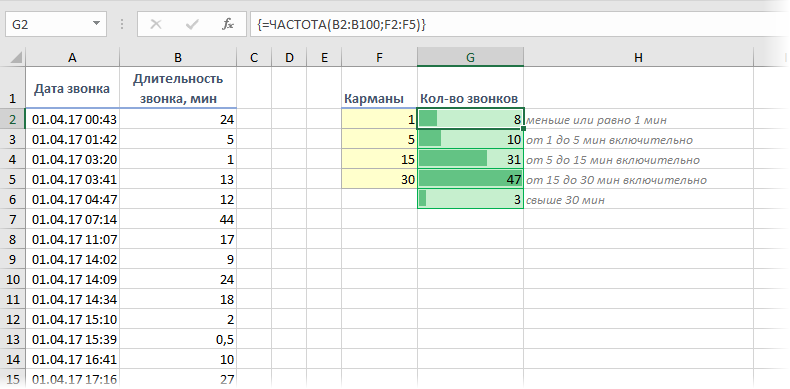
Для решения подобной задачи можно воспользоваться функцией ЧАСТОТА (FREQUENCY) . Ее синтаксис прост:

=ЧАСТОТА( Данные ; Карманы )

• Карманы — диапазон с границами интервалов, попадание в которые нас интересует
• Данные — диапазон с исходными числовыми значениями, которые мы анализируем

Обратите внимание, что эта функция игнорирует пустые ячейки и ячейки с текстом, т.е. работает только с числами.

Для использования функции ЧАСТОТА нужно:

1. заранее подготовить ячейки с интересующими нас интервалами-карманами (желтые F2:F5 в нашем примере)
2. выделить пустой диапазон ячеек (G2:G6) по размеру на одну ячейку больший, чем диапазон карманов (F2:F5)
3. ввести функцию ЧАСТОТА и нажать в конце сочетание Ctrl+Shift+Enter, т.е. ввести ее как формулу массива

Во всех предварительно выделенных ячейках посчитается количество попаданий в заданные интервалы. Само-собой, для реализации подобной задачи можно использовать и другие способы (функцию СЧЁТЕСЛИ, сводные таблицы и т.д.), но этот вариант весьма хорош.

Кроме того, с помощью функции ЧАСТОТА можно легко подсчитывать количество уникальных чисел в наборе с помощью простой формулы массива:

Функция ЧАСТОТА используется для определения количества вхождения определенных величин в заданный интервал и возвращает данные в виде массива значений. Используя функцию ЧАСТОТА, мы узнаем, как посчитать частоту в Excel.

Пример использования функции ЧАСТОТА в Excel

Пример 1. Студенты одной из групп в университете сдали экзамен по физике. При оценке качества сдачи экзамена используется 100-бальная система. Для определения окончательной оценки по 5-бальной системе используют следующие критерии:

1. От 0 до 50 баллов – экзамен не сдан.
2. От 51 до 65 баллов – оценка 3.
3. От 66 до 85 баллов – оценка 4.
4. Свыше 86 баллов – оценка 5.

Для статистики необходимо определить, сколько студентов получили 5, 4, 3 баллов и количество тех, кому не удалось сдать экзамен.

Внесем данные в таблицу:

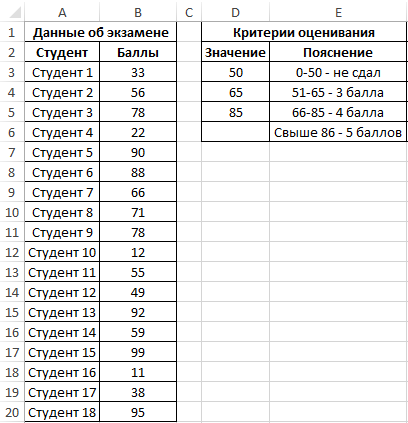
Для решения выделим области из 4 ячеек и введем следующую функцию:

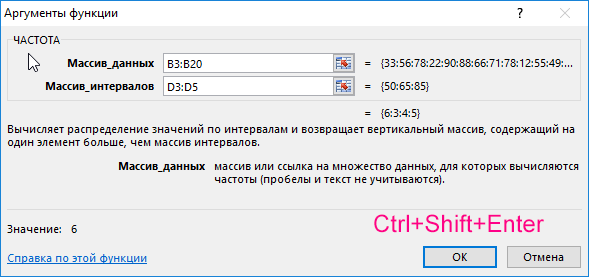
• B3:B20 – массив данных об оценках студентов;
• D3:D5 – массив критериев нахождения частоты вхождений в массиве данных об оценках.

Выделяем диапазон F3:F6 жмем сначала клавишу F2, а потом комбинацию клавиш Ctrl+Shift+Enter, чтобы функция ЧАСТОТА была выполнена в массиве. Подтверждением того что все сделано правильно будут служить фигурные скобки <> в строке формул по краям. Это значит, что формула выполняется в массиве. В результате получим:

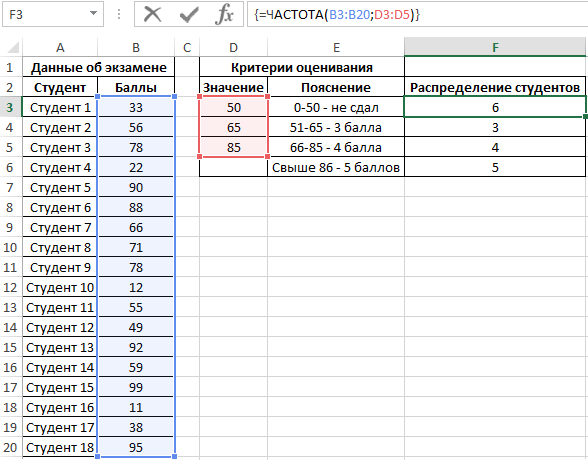
То есть, 6 студентов не сдали экзамен, оценки 3, 4 и 5 получили 3, 4 и 5 студентов соответственно.

Пример определения вероятности используя функцию ЧАСТОТА в Excel

Пример 2. Известно то, что если существует только два возможных варианта развития событий, вероятности первого и второго равны 0,5 соответственно. Например, вероятности выпадения «орла» или «решки» у подброшенной монетки равны ½ и ½ (если пренебречь возможностью падения монетки на ребро). Аналогичное расчетное распределение вероятностей характерно для следующей функции СЛУЧМЕЖДУ(1;2), которая возвращает случайное число в интервале от 1 до 2. Было проведено 20 вычислений с использованием данной функции. Определить фактические вероятности появления чисел 1 и 2 соответственно на основании полученных результатов.

Заполним исходную таблицу случайными значениями от 1-го до 2-ух:

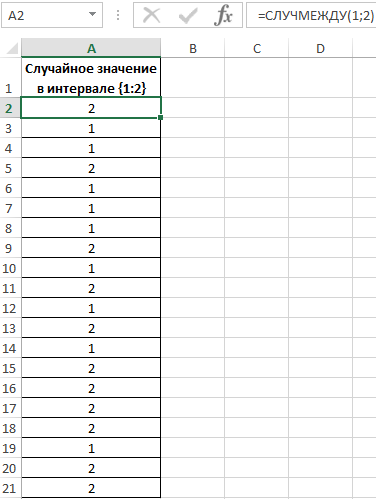
Для определения случайных значений в исходной таблице была использована специальная функция:

Для определения количества сгенерированных 1 и 2 используем функцию:

• A2:A21 – массив сгенерированных функцией =СЛУЧМЕЖДУ(1;2) значений;
• 1 – критерий поиска (функция ЧАСТОТА ищет значения от 0 до 1 включительно и значения >1).

В результате получим:

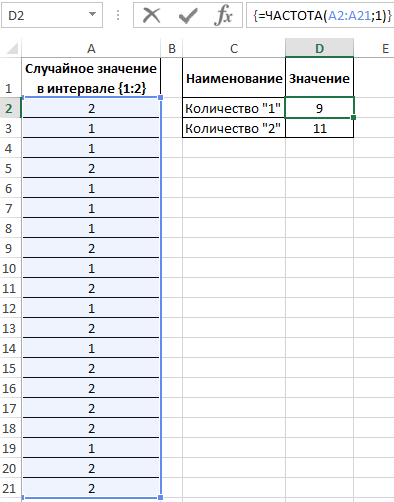
Вычислим вероятности, разделив количество событий каждого типа на общее их число:

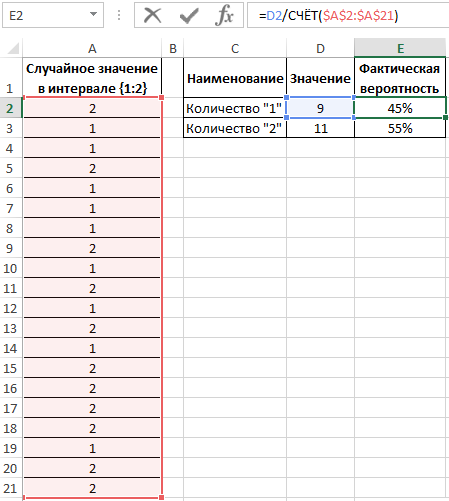
Для подсчета количества событий используем функцию =СЧЁТ($A$2:$A$21). Или можно просто разделить на значение 20. Если заранее не известно количество событий и размер диапазона со случайными значениями, тогда можно использовать в аргументах функции СЧЁТ ссылку на целый столбец: =СЧЁТ(A:A). Таким образом будет автоматически подсчитывается количество чисел в столбце A.

Вероятности выпадения «1» и «2» — 0,45 и 0,55 соответственно. Не забудьте присвоить ячейкам E2:E3 процентный формат для отображения их значений в процентах: 45% и 55%.

Теперь воспользуемся более сложной формулой для вычисления максимальной частоты повторов:

1)*СТРОКА($A$2:$A$21)))-1′ >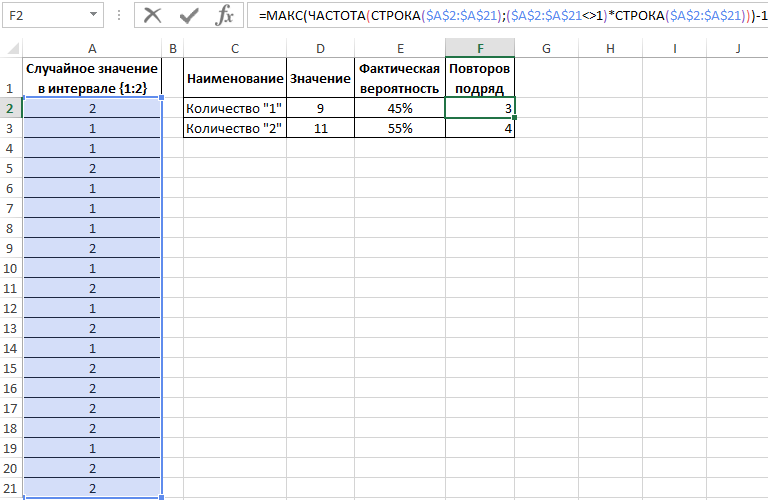

Формулы в ячейках F2 и F3 отличаются только одним лишь числом после оператора сравнения «не равно»: <>1 и <>2.

Интересный факт! С помощью данной формулы можно легко проверить почему не работает стратегия удвоения ставок в рулетке казино. Данную стратегию управления ставками в азартных играх называют еще Мартингейл. Дело в том, что количество случайных повторов подряд может достигать 18-ти раз и более, то есть восемнадцать раз подряд красные или черные. Например, если ставку в 2 доллара 18 раз удваивать – это уже более пол миллиона долларов «просадки». Это уже провал по любым техникам планирования рисков. Так же следует учитывать, что кроме «черные» и «красные» иногда выпадает еще и «зеро», что окончательно уничтожает все шансы. Так же интересно, что сумма всех чисел в рулетке от 0 до 36 равна 666.

Как посчитать неповторяющиеся значения в Excel?

Пример 3. Определить количество уникальных вхождений в массив числовых данных, то есть не повторяющихся значений.

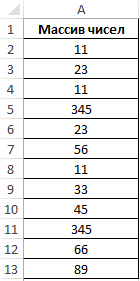
Определим искомую величину с помощью формулы:

В данном случае функция ЧАСТОТА выполняет проверку наличия каждого из элементов массива данных в этом же массиве данных (оба аргумента совпадают). С помощью функции ЕСЛИ задано условие, которое имеет следующий смысл:

1. Если искомый элемент содержится в диапазоне значений, вместо фактического количества вхождений будет возвращено 1;
2. Если искомого элемента нет – будет возвращен 0 (нуль).

Полученное значение (количество единиц) суммируется.

В результате получим:

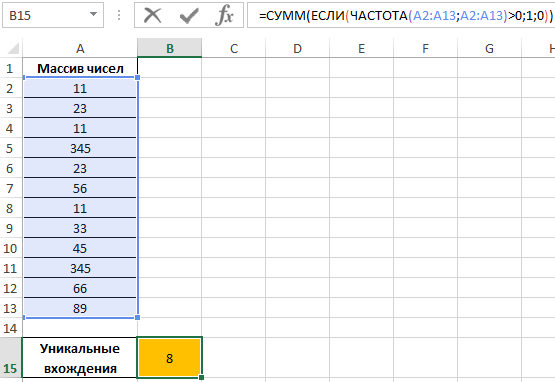
То есть, в указанном массиве содержится 8 уникальных значений.

Функция ЧАСТОТА в Excel и особенности ее синтаксиса

Данная функция имеет следующую синтаксическую запись:

Описание аргументов функции (оба являются обязательными для заполнения):

• массив_данных – данные в форме массива либо ссылка на диапазон значений, для которых необходимо определить частоты.
• массив_интервалов — данные в формате массива либо ссылка не множество значений, в которые группируются значения первого аргумента данной функции.

1. Если в качестве аргумента массив_интервалов был передан пустой массив или ссылка на диапазон пустых значений, результатом выполнения функции ЧАСТОТА будет являться число элементов, входящих диапазон данных, которые были переданы в качестве первого аргумента.
2. При использовании функции ЧАСТОТА в качестве обычной функции Excel будет возвращено единственное значение, соответствующее первому вхождению в массив_интервалов (то есть, первому критерию поиска частоты вхождения).
3. Массив возвращаемых данной функцией элементов содержит на один элемент больше, чем количество элементов, содержащихся в массив_интервалов. Это происходит потому, что функция ЧАСТОТА вычисляет также количество вхождений величин, значения которых превышают верхнюю границу интервалов. Например, в наборе данных 2,7, 10, 13, 18, 4, 33, 26 необходимо найти количество вхождений величин из диапазонов от 1 до 10, от 11 до 20, от 21 до 30 и более 30. Массив интервалов должен содержать только их граничные значения, то есть 10, 20 и 30. Функция может быть записана в следующем виде: =ЧАСТОТА(<2;7;10;13;18;4;33;26>;<10;20;30>), а результатом ее выполнения будет столбец из четырех ячеек, которые содержат следующие значения: 4,2, 1, 1. Последнее значение соответствует количеству вхождений чисел > 30 в массив_данных. Такое число действительно является единственным – это 33.
4. Если в состав массив_данных входят ячейки, содержащие пустые значения или текст, они будут пропущены функцией ЧАСТОТА в процессе вычислений.

Функция может использоваться для выполнения статистического анализа, например, с целью определения наиболее востребованных для покупателей наименований продукции.

Данная функция должна быть использована как формула массива, поскольку возвращаемые ей данные имеют форму массива. Для выполнения обычных формул после их ввода необходимо нажать кнопку Enter. В данном случае требуется использовать комбинацию клавиш Ctrl+Shift+Enter.