Числовая информация в памяти компьютера кодируется

Десятичное и двоичное представление чисел

Для работы с числовой информацией мы пользуемся системой счисления, содержащей десять цифр: от $0$ до $9$. Эта система называется десятичной.

Кроме цифр, в десятичной системе большое значение имеют разряды. Подсчитывая количество чего-нибудь и дойдя до самой большой из доступных нам цифр (до $9$), мы вводим второй разряд и дальше каждое последующее число формируем из двух цифр. Дойдя до $99$, мы вынуждены вводить третий разряд. В пределах трех разрядов мы можем досчитать уже до $999$ и т.д.

Таким образом, используя всего десять цифр и вводя дополнительные разряды, мы можем записывать и проводить математические операции с любыми, даже самыми большими числами.

Компьютер ведет подсчет аналогичным образом, но имеет в своем распоряжении всего две цифры — логический ноль (отсутствие у бита какого-то свойства) и логическую единицу (наличие у бита этого свойства).

Система счисления, использующая только две цифры, называется двоичной. При подсчете в двоичной системе добавлять каждый следующий разряд приходится гораздо чаще, чем в десятичной.

Попробуй обратиться за помощью к преподавателям

Вот таблица первых десяти чисел в каждой из этих систем счисления:

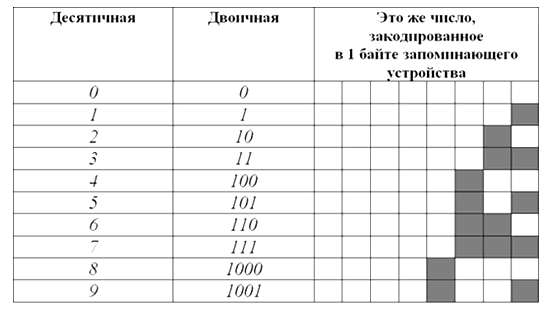
Как видите, в десятичной системе счисления для отображения любой из первых десяти цифр достаточно $1$ разряда. В двоичной системе для тех же целей потребуется уже $4$ разряда.

Соответственно, для кодирования этой же информации в виде двоичного кода нужен носитель емкостью как минимум $4$ бита ($0,5$ байта). Человеческий мозг, привыкший к десятичной системе счисления, плохо воспринимает систему двоичную. Хотя обе они построены на одинаковых принципах и отличаются лишь количеством используемых цифр. В двоичной системе точно так же можно осуществлять любые арифметические операции с любыми числами. Главный ее минус — необходимость иметь дело с большим количеством разрядов.

Задай вопрос специалистам и получи
ответ уже через 15 минут!

Так, самое большое десятичное число, которое можно отобразить в 8 разрядах двоичной системы — $255$, в $16$ разрядах – $65535$, в $24$ разрядах – $16777215$.

Алгоритмы кодирования чисел в двоичной системе счисления

Компьютер, кодируя числа в двоичный код, основывается на двоичной системе счисления. Но, в зависимости от особенностей чисел, может использовать разные алгоритмы:

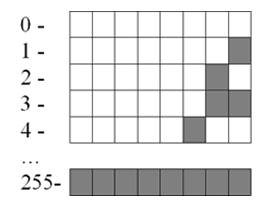
Небольшие целые числа без знака.

Для сохранения каждого такого числа на запоминающем устройстве, как правило, выделяется $1$ байт ($8$ битов). Запись осуществляется в полной аналогии с двоичной системой счисления.

Целые десятичные числа без знака, сохраненные на носителе в двоичном коде, будут выглядеть примерно так:

Большие целые числа и числа со знаком.

Для записи каждого такого числа на запоминающем устройстве, как правило, отводится $2$-байтний блок ($16$ битов).

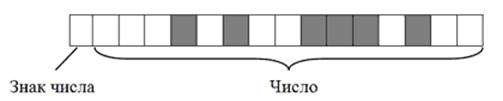
Старший бит блока (тот, что крайний слева) отводится под запись знака числа и в кодировании самого числа не участвует. Если число со знаком "плюс", этот бит остается пустым, если со знаком "минус" – в него записывается логическая единица. Число же кодируется в оставшихся 15 битах. Например, алгоритм кодирования числа $+2676$ будет следующим:

• Перевести число $2676$ из десятичной системы счисления в двоичную. В итоге получится $101001110100$;
• Записать полученное двоичное число в первые $15$ бит $16$-битного блока (начиная с правого края). Последний, $16$-й бит, должен остаться пустым, поскольку кодируемое число имеет знак $+$.

В итоге $+2676$ в двоичном коде на запоминающем устройстве будет выглядеть так:

Примечательно, что в двоичном коде присвоение числу отрицательного значения предусматривает не только изменение старшего бита. Осуществляется также инвертирование всех остальных его битов.

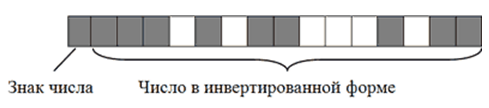
Чтобы было понятно, рассмотрим алгоритм кодирования числа $-2676$:

1. Перевести число $2676$ из десятичной системы счисления в двоичную. Получим все тоже двоичное число $101001110100$;
2. Записать полученное двоичное число в первые $15$ бит $16$-битного блока. Затем инвертировать, то есть, изменить на противоположное, значение каждого из $15$ битов;
3. Записать в $16$-й бит логическую единицу, поскольку кодируемое число имеет отрицательное значение.

В итоге $-2676$ на запоминающем устройстве в двоичном коде будет иметь следующий вид:

Запись отрицательных чисел в инвертированной форме позволяет заменить все операции вычитания, в которых они участвуют, операциями сложения. Это необходимо для нормальной работы компьютерного процессора.

Максимальным десятичным числом, которое можно закодировать в $15$ битах запоминающего устройства, является $32767$. Иногда для записи чисел по этому алгоритму выделяются $4$-байтные блоки. В таком случае для кодирования каждого числа будет использоваться $31$ бит плюс $1$ бит для кодирования знака числа. Тогда максимальным десятичным числом, сохраняемым в каждую ячейку, будет $2147483647$ (со знаком плюс или минус).

Дробные числа со знаком.

Дробные числа на запоминающем устройстве в двоичном коде кодируются в виде так называемых чисел с плавающей запятой (точкой). Алгоритм их кодирования сложнее, чем рассмотренные выше. Тем не менее, попытаемся разобраться.

Для записи каждого числа с плавающей запятой компьютер чаще всего выделяет $4$-байтную ячейку ($32$ бита):

• в старшем бите этой ячейки (тот, что крайний слева) записывается знак числа. Если число отрицательное, в этот бит записывается логическая единица, если оно со знаком "плюс" – бит остается пустым.
• во втором слева бите аналогичным образом записывается знак порядка (что такое порядок поймете позже);
• в следующих за ним $7$ битах записывается значение порядка.
• в оставшихся $23$ битах записывается так называемая мантисса числа.

Чтобы стало понятно, что такое порядок, мантисса и зачем они нужны, переведем в двоичный код десятичное число $6,25$.

Порядок кодирования будет примерно следующим:

1. Перевести десятичное число в двоичное (десятичное $6,25$ равно двоичному $110,01$);
2. Определить мантиссу числа. Для этого в числе необходимо передвинуть запятую в нужном направлении, чтобы слева от нее не осталось ни одной единицы. В нашем случае запятую придется передвинуть на три знака влево. В итоге, получим мантиссу, $11001$;
3. Определить значение и знак порядка. Значение порядка – это количество символов, на которое была сдвинута запятая для получения мантиссы. В нашем случае оно равно $3$ (или $11$ в двоичной форме);

Знак порядка – это направление, в котором пришлось двигать запятую: влево – "плюс", вправо – "минус". В нашем примере запятая двигалась влево, поэтому знак порядка – "плюс".

Таким образом, порядок двоичного числа $110,01$ будет равен $+11$, а его мантисса, $11001$. В результате в двоичном коде на запоминающем устройстве это число будет записано следующим образом

Обратите внимание, что мантисса в двоичном коде записывается, начиная с первого после запятой знака, а сама запятая упускается. Числа с плавающей запятой, кодируемые в $32$ битах, называю числами одинарной точности. Когда для записи числа $32$-битной ячейки недостаточно, компьютер может использовать ячейку из $64$ битов. Число с плавающей запятой, закодированное в такой ячейке, называется числом двойной точности.

Так и не нашли ответ
на свой вопрос?

Просто напиши с чем тебе
нужна помощь

Мы познакомились с системами счисления — способами кодирования чисел. Числа дают информацию о количестве предметов. Эта информация должна быть закодирована, представлена в какой-то системе счисления. Какой из известных способов выбрать, зависит от решаемой задачи.
До недавнего времени на компьютерах в основном обрабатывалась числовая и текстовая информация. Но большую часть информации о внешнем мире человек получает в виде изображения и звука. При этом более важным оказывается изображение. Помните пословицу: “Лучше один раз увидеть, чем сто раз услышать”. Поэтому сегодня компьютеры начинают всё активнее работать с изображением и звуком. Способы кодирования такой информации будут обязательно нами рассмотрены.

Двоичное кодирование числовой и текстовой информации.

Любая информация кодируется в ЭВМ с помощью последовательностей двух цифр — 0 и 1. ЭВМ хранит и обрабатывает информацию в виде комбинации электрических сигналов: напряжение 0.4В-0.6В соответствует логическому нулю, а напряжение 2.4В-2.7В — логической единице. Последовательности из 0 и 1 называются двоичными кодами, а цифры 0 и 1 — битами (двоичными разрядами). Такое кодирование информации на компьютере называется двоичным кодированием. Таким образом, двоичное кодирование — это кодирование с минимально возможным числом элементарных символов, кодирование самыми простыми средствами. Тем оно и замечательно с теоретической точки зрения.
Инженеров двоичное кодирование информации привлекает тем, что легко реализуется технически. Электронные схемы для обработки двоичных кодов должны находиться только в одном из двух состояний: есть сигнал/нет сигнала или высокое напряжение/низкое напряжение.
ЭВМ в своей работе оперируют действительными и целыми числами, представленными в виде двух, четырёх, восьми и даже десяти байт. Для представления знака числа при счёте используется дополнительный знаковый разряд, который обычно располагается перед числовыми разрядами. Для положительных чисел значение знакового разряда равно 0, а для отрицательных чисел — 1. Для записи внутреннего представления целого отрицательного числа (-N) необходимо:
1) получить дополнительный код числа N заменой 0 на 1 и 1 на 0;
2) к полученному числу прибавить 1.

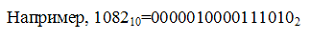
Так как одного байта для представления этого числа недостаточно, оно представлено в виде 2 байт или 16 бит, его дополнительный код: 1111101111000101, следовательно, -1082=1111101111000110.
Если бы ПК мог работать только с одиночными байтами, пользы от него было бы немного. Реально ПК работает с числами, которые записываются двумя, четырьмя, восемью и даже десятью байтами.
Начиная с конца 60-х годов компьютеры всё больше стали использоваться для обработки текстовой информации. Для представления текстовой информации обычно используется 256 различных символов, например большие и малые буквы латинского алфавита, цифры, знаки препинания и т.д. В большинстве современных ЭВМ каждому символу соответствует последовательность из восьми нулей и единиц, называемая байтом.
Байт – это восьмиразрядная комбинация нулей и единиц.
При кодировании информации в этих электронно-вычислительных машинах используют 256 разных последовательностей из 8 нулей и единиц, что позволяет закодировать 256 символов. Например большая русская буква «М» имеет код 11101101, буква «И» — код 11101001, буква «Р» — код 11110010. Таким образом, слово «МИР» кодируется последовательностью из 24 бит или 3 байт: 111011011110100111110010.
Количество бит в сообщении называется информационным объёмом сообщения. Это интересно!

Первоначально в ЭВМ использовался лишь латинский алфавит. В нём 26 букв. Так что для обозначения каждой хватило бы пяти импульсов (битов). Но в тексте есть знаки препинания, десятичные цифры и др. Поэтому в первых англоязычных компьютерах байт — машинный слог — включал шесть битов. Затем семь — не только чтобы отличать большие буквы от малых, но и для увеличения числа кодов управления принтерами, сигнальными лампочками и прочим оборудованием. В 1964 году появились мощные IBM-360, в которых окончательно байт стал равен восьми битам. Последний восьмой бит был необходим для символов псевдографики. Присвоение символу конкретного двоичного кода — это вопрос соглашения, которое фиксируется в кодовой таблице. К сожалению, существует пять различных кодировок русских букв, поэтому тексты, созданные в одной кодировке, не будут правильно отражаться в другой.
Хронологически одним из первых стандартов кодирования русских букв на компьютерах был КОИ8 («Код обмена информацией, 8 битный»). Наиболее распространённая кодировка — это стандартная кириллическая кодировка Microsoft Windows, обозначаемая сокращением СР1251 («СР» означает «Code Page» или «кодовая страница»). Фирма Apple разработала для компьютеров Macintosh собственную кодировку русских букв (Мас). Международная организация по стандартизации (International Standards Organization, ISO) утвердила в качестве стандарта для русского языка кодировку ISO 8859-5. Наконец, появился новый международный стандарт Unicode, который отводит на каждый символ не один байт, а два, и поэтому с его помощью можно закодировать не 256 символов, а целых 65536.
Все эти кодировки продолжают кодовую таблицу стандарта ASCII (Американский стандартный код для информационного обмена), кодирующую 128 символов.
Таблица символов ASCII:

код	символ	код	символ	код	символ	код	символ	код	символ	код	символ
32	Пробел	48	.	64	@	80	P	96	‘	112	p
33	!	49		65	A	81	Q	97	a	113	q
34	"	50	1	66	B	82	R	98	b	114	r
35	#	51	2	67	C	83	S	99	c	115	s
36	$	52	3	68	D	84	T	100	d	116	t
37	%	53	4	69	E	85	U	101	e	117	u
38	&	54	5	70	F	86	V	102	f	118	v
39	‘	55	6	71	G	87	W	103	g	119	w
40	(	56	7	72	H	88	X	104	h	120	x
41	)	57	8	73	I	89	Y	105	i	121	y
42	*	58	9	74	J	90	Z	106	j	122	z
43	+	59	:	75	K	91	[	107	k	123	<
44	,	60	;	76	L	92		108	l	124	|
45	—	61	78	N	94	^	110	n	126
47	/	63	?	79	O	95	_	111	o	127	DEL

Двоичное кодирование текста происходит следующим образом: при нажатии на клавишу в компьютер передаётся определённая последовательность электрических импульсов, причём каждому символу соответствует своя последовательность электрических импульсов (нулей и единиц на машинном языке). Программа драйвер клавиатуры и экрана по кодовой таблице определяет символ и создаёт его изображение на экране. Таким образом, тексты и числа хранятся в памяти компьютера в двоичном коде и программным способом преобразуются в изображения на экране.

Двоичное кодирование графической информации.

С 80-х годов бурно развивается технология обработки на компьютере графической информации. Компьютерная графика широко используется в компьютерном моделировании в научных исследованиях, компьютерных тренажёрах, компьютерной анимации, деловой графике, играх и т.д.
Графическая информация на экране дисплея представляется в виде изображения, которое формируется из точек (пикселей). Всмотритесь в газетную фотографию, и вы увидите, что она тоже состоит из мельчайших точек. Если это только чёрные и белые точки, то каждую из них можно закодировать 1 битом. Но если на фотографии оттенки, то два бита позволяет закодировать 4 оттенка точек: 00 — белый цвет, 01 — светло-серый, 10 — тёмно-серый, 11 — чёрный. Три бита позволяют закодировать 8 оттенков и т.д.
Количество бит, необходимое для кодирования одного оттенка цвета, называется глубиной цвета.

В современных компьютерах разрешающая способность (количество точек на экране), а также количество цветов зависит от видеоадаптера и может изменяться программно.
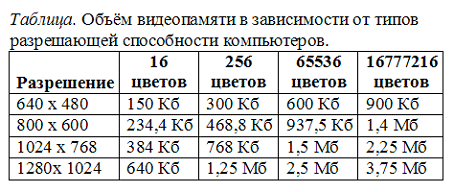
Цветные изображения могут иметь различные режимы: 16 цветов, 256 цветов, 65536 цветов (high color), 16777216 цветов (true color). На одну точку для режима high color необходимо 16 бит или 2 байта.
Наиболее распространённой разрешающей способностью экрана является разрешение 800 на 600 точек, т.е. 480000 точек. Рассчитаем необходимый для режима high color объём видеопамяти: 2 байт *480000=960000 байт.
Для измерения объёма информации используются и более крупные единицы:

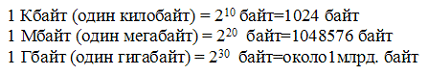
Следовательно, 960000 байт приблизительно равно 937,5 Кбайт. Если человек говорит по восемь часов в день без перерыва, то за 70 лет жизни он наговорит около 10 гигабайт информации (это 5 миллионов страниц — стопка бумаги высотой 500 метров).
Скорость передачи информации — это количество битов, передаваемых в 1 секунду. Скорость передачи 1 бит в 1 секунду называется 1 бод.

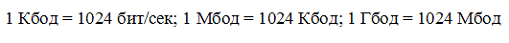
В видеопамяти компьютера хранится битовая карта, являющаяся двоичным кодом изображения, откуда она считывается процессором (не реже 50 раз в секунду) и отображается на экран.

Двоичное кодирование звуковой информации.

С начала 90-х годов персональные компьютеры получили возможность работать со звуковой информацией. Каждый компьютер, имеющий звуковую плату, может сохранять в виде файлов (файл — это определённое количество информации, хранящееся на диске и имеющее имя) и воспроизводить звуковую информацию. С помощью специальных программных средств (редакторов аудио файлов) открываются широкие возможности по созданию, редактированию и прослушиванию звуковых файлов. Создаются программы распознавания речи, и появляется возможность управления компьютером голосом.
Именно звуковая плата (карта) преобразует аналоговый сигнал в дискретную фонограмму и наоборот, «оцифрованный» звук – в аналоговый (непрерывный) сигнал, который поступает на вход динамика.

При двоичном кодировании аналогового звукового сигнала непрерывный сигнал дискретизируется, т.е. заменяется серией его отдельных выборок — отсчётов. Качество двоичного кодирования зависит от двух параметров: количества дискретных уровней сигнала и количества выборок в секунду. Количество выборок или частота дискретизации в аудиоадаптерах бывает различной: 11 кГц, 22 кГц, 44,1 кГц и др. Если количество уровней равно 65536, то на один звуковой сигнал рассчитано 16 бит (216). 16-разрядный аудиоадаптер точнее кодирует и воспроизводит звук, чем 8-разрядный.
Количество бит, необходимое для кодирования одного уровня звука, называется глубиной звука.
Объём моноаудиофайла (в байтах) определяется по формуле:

При стереофоническом звучании объём аудиофайла удваивается, при квадрофоническом звучании – учетверяется.
По мере усложнения программ и увеличения их функций, а также появления мультимедиа-приложений, растёт функциональный объём программ и данных. Если в середине 80-х годов обычный объём программ и данных составлял десятки и лишь иногда сотни килобайт, то в середине 90-х годов он стал составлять десятки мегабайт. Соответственно растёт объём оперативной памяти.

Современный компьютер может обрабатывать числовую, текстовую, графическую, звуковую и видео информацию. Все эти виды информации в компьютере представлены в двоичном коде, т. е. используется алфавит мощностью два символа (0 и 1). Связано это с тем, что удобно представлять информацию в виде последовательности электрических импульсов: импульс отсутствует (0), импульс есть (1). Такое кодирование принято называть двоичным, а сами логические последовательности нулей и единиц — машинным языком.

Каждая цифра машинного двоичного кода несет количество информации равное одному биту.

Данный вывод можно сделать, рассматривая цифры машинного алфавита, как равновероятные события. При записи двоичной цифры можно реализовать выбор только одного из двух возможных состояний, а, значит, она несет количество информации равное 1 бит. Следовательно, две цифры несут информацию 2 бита, четыре разряда —4 бита и т. д. Чтобы определить количество информации в битах, достаточно определить количество цифр в двоичном машинном коде.

Кодирование текстовой информации

В настоящее время большая часть пользователей при помощи компьютера обрабатывает текстовую информацию, которая состоит из символов: букв, цифр, знаков препинания и др.

На основании одной ячейки информационной ёмкостью 1 бит можно закодировать только 2 различных состояния. Для того чтобы каждый символ, который можно ввести с клавиатуры в латинском регистре, получил свой уникальный двоичный код, требуется 7 бит. На основании последовательности из 7 бит, в соответствии с формулой Хартли, может быть получено N=2 7 =128 различных комбинаций из нулей и единиц, т.е. двоичных кодов. Поставив в соответствие каждому символу его двоичный код, мы получим кодировочную таблицу. Человек оперирует символами, компьютер – их двоичными кодами.

Для латинской раскладки клавиатуры такая кодировочная таблица одна на весь мир, поэтому текст, набранный с использованием латинской раскладки, будет адекватно отображен на любом компьютере. Эта таблица носит название ASCII (American Standard Code of Information Interchange) по-английски произносится [э́ски], по-русски произносится [а́ски]. Ниже приводится вся таблица ASCII, коды в которой указаны в десятичном виде. По ней можно определить, что когда вы вводите с клавиатуры, скажем, символ “*”, компьютер его воспринимает как код 42(10), в свою очередь 42(10)=101010(2) – это и есть двоичный код символа “*”. Коды с 0 по 31 в этой таблице не задействованы.