Частота дискретизации аналогового сигнала

Частота дискретизации (или частота семплирования, англ. sample rate) — частота взятия отсчётов непрерывного по времени сигнала при его дискретизации (в частности, аналого-цифровым преобразователем). Измеряется в герцах.

Термин применяется и при обратном, цифро-аналоговом преобразовании, особенно если частота дискретизации прямого и обратного преобразования выбрана разной (Данный приём, называемый также «Масштабированием времени», встречается, например, при анализе сверхнизкочастотных звуков, издаваемых морскими животными).

Чем выше частота дискретизации, тем более широкий спектр сигнала может быть представлен в дискретном сигнале. Как следует из теоремы Котельникова, для того, чтобы однозначно восстановить исходный сигнал, частота дискретизации должна более чем в два раза превышать наибольшую частоту в спектре сигнала.

Некоторые из используемых частот дискретизации звука [1] :

• 8 000 Гц — телефон, достаточно для речи, кодек Nellymoser;
• 11 025 Гц — четверть Audio CD, достаточно для передачи речи;
• 16 000 Гц;
• 22 050 Гц — половина Audio CD, достаточно для передачи качества радио;
• 32 000 Гц;
• 44 100 Гц — используется в Audio CD. Выбрано Sony из соображений совместимости со стандартом PAL, за счёт записи 3 значений на линию картинки кадра × 588 линий на кадр × 25 кадров в секунду, и достаточности (по теореме Котельникова) для качественного покрытия всего диапазона частот, различаемых человеком на слух (20 Гц — 20 КГц);
• 48 000 Гц — DVD, DAT;
• 96 000 Гц — DVD-Audio (MLP 5.1);
• 192 000 Гц — DVD-Audio (MLP 2.0);
• 2 822 400 Гц — SACD, процесс однобитной дельта-сигма модуляции, известный как DSD — Direct Stream Digital, совместно разработан компаниями Sony и Philips;
• 5 644 800 Гц — DSD с удвоенной частотой дискретизации, однобитный Direct Stream Digital с частотой дискретизации вдвое больше, чем у SACD. Используется в некоторых профессиональных устройствах записи DSD.

Итак, преобразование аналогового сигнала в цифровой состоит из двух этапов: дискретизации по времени и квантования по амплитуде. Дискретизация по времени означает, что сигнал представляется рядом своих отсчетов (семплов), взятых через равные промежутки времени. Например, когда мы говорим, что частота дискретизации 44,1 кГц, то это значит, что сигнал измеряется 44100 раз в течении секунды

Основной вопрос на первом этапе преобразования аналогового сигнала в цифровой (оцифровки) состоит в выборе частоты дискретизации аналогового сигнала. Как уже было сказано, чем больше частота — тем точнее соответствует цифровой сигнал аналоговому. Однако, пропорционально увеличению частоты возрастают:

а) интенсивность потока цифровых данных, а пропускные возможности интерфейсов не безграничны, особенно если записывается/воспроизводится одновременно несколько каналов;

б) вычислительная нагрузка на цифровые процессоры эффектов, а их вычислительные возможности также ограничены;

в) объем памяти, необходимой для хранения цифрового сигнала. Очевидно, что необходим компромисс.

От выбора частоты дискретизации зависит частотный диапазон полученного цифрового звука или максимальная частота аналогового сигнала, правильно представленная в цифровом. Считается, что диапазон частот, которые слышит человек, составляет от 20 до 20000 Гц. Согласно известной теореме Котельникова, для того, чтобы аналоговый (непрерывный по времени) сигнал можно было точно восстановить по его отсчетам, частота дискретизации должна быть как минимум вдвое больше максимальной звуковой частоты. Таким образом, если реальный аналоговый сигнал, который мы собираемся преобразовать в цифровую форму, содержит частотные компоненты от 0 Гц до 20 кГц, то частота дискретизации такого сигнала должна быть не меньше, чем 40 кГц. Сегодня самыми распространенными частотами дискретизации являются 44,1 кГц (CD) и 48 кГц (DAT). Впрочем, в последнее время идет немало разговоров о том, что обертоны, расположенные свыше 20 кГц, вносят немалый вклад в звучание и в результате появляются преобразователи, использующие частоты дискретизации 96 кГц и 192 кГц, а в недалеком будущем ожидается появление и систем с частотой 384 кГц.

Тем не менее, исходный аналоговый сигнал обычно имеет спектр, сосредоточенный в основном в полосе частот от 20 Гц до, примерно, 20 кГц. Однако, кроме того в сигнале обычно содержатся помехи с частотами до нескольких сот килогерц. Это различные трудно устранимые наводки от компьютерной техники, промышленных и электробытовых приборов, трамваев, троллейбусов и т. д. На рисунке внизу вы видите спектр исходного аналогового сигнала.

В процессе дискретизации частотный спектр аналогового сигнала претерпевает значительные изменения. Он становится периодическим. Спектр исходного сигнала периодически повторяется с периодом равным частоте дискретизации. Результат этого процесса показан на рисунке внизу. Высокочастотные компоненты исходного сигнала (помехи) попадают в низкочастотную часть спектра.

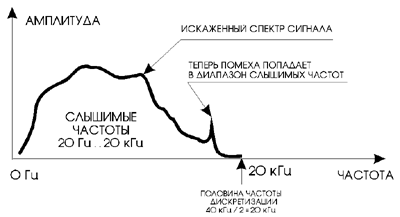
Все это выглядит весьма непривычно, если не сказать, что вообще противоречит здравому смыслу! Получается, что происходит дискретизация высокочастотных сигналов, лежащих значительно выше не только частоты Найквиста, но и самой частоты дискретизации. На первый взгляд это даже противоречит упомянутой выше теореме Котельникова. Однако это происходит именно так.

Второе изменение спектра заключается в его расширении. В отличии от "свертки" этот факт уже не противоречит здравому смыслу и вполне очевиден. После дискретизации относительно низкочастотный исходный аналоговый сигнал представляет из себя последовательный временной ряд очень узких импульсов с разной амплитудой и с очень широким спектром до нескольких мегагерц (математический факт — чем уже импульс, тем шире его спектр). Поэтому и в целом спектр такой последовательности импульсов расширяется до тех же нескольких мегагерц. Таким образом, спектр дискретизированного сигнала значительно шире спектра исходного аналогового сигнала.

Так как весь исходный спектр свернулся в полосу частот от 0 Гц до частоты Котельникова, то логично и естественно, что расширение спектра происходит дублированием спектра из полосы от 0 Гц до частоты Котельникова.

Итак, реальные аналоговые сигналы часто содержат высокочастотные составляющие, плохо поддающиеся оцифровке на стандартных частотах 44,1 кГц или 48 кГц. Поэтому перед дискретизацией необходима аналоговая фильтрация, то есть удаление всех частот выше частоты Котельникова, являющаяся довольно сложной задачей. Аналоговые фильтры не могут пропустить, скажем, все частоты от 0 Гц до 24 кГц и подавить все частоты выше 24 кГц. Аналоговый фильтр низких частот начинает подавлять высокие частоты начиная с некоторой частоты, называемой частотой среза. Подавление плавно усиливается с ростом частоты. Поэтому, чтобы добиться отсутствия частот выше 24 кГц необходимо устанавливать частоту среза фильтра примерно на 16..20 кГц, а это уже плохо, так как будут ослаблены полезные частоты в слышимом диапазоне 16..20 кГц. Еще одна неприятность состоит в том, что чем более узкой мы пытаемся сделать переходную область между полосой пропускания и полосой подавления фильтра, тем сильнее вносимые фазовые искажения, длиннее переходный процесс (фильтр начинает "звенеть") и тем сложнее и капризнее в настройке такой аналоговый фильтр.

В современных АЦП эта проблема решается методом дискретизации на повышенной частоте. По этому методу диапазон частот входного аналогового сигнала ограничивается с помощью сравнительно несложного аналогового фильтра. Причем частота среза фильтра выбирается значительно выше высшей полезной частоты, а переходная полоса фильтра делается достаточно широкой.

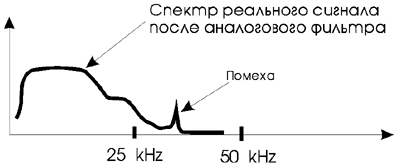
Таким образом, исключаются и завал полезных высших частот, и фазовые искажения, характерные для аналоговых фильтров с узкой переходной полосой. Далее, отфильтрованный, с ограниченным по частоте спектром, сигнал дискретизируется на достаточно высокой частоте, исключающей наложение и искажение спектра — алиазинг (aliasing). Затем дискретные отсчеты сигнала преобразуются в последовательность чисел с помощью АЦП. После этого мы имеем поток цифровых данных, представляющих аналоговый сигнал, включающий как полезные, так и нежелательные высокочастотные компоненты и помехи. Эти цифровые данные пропускаются через цифровой фильтр с очень узкой переходной полосой и очень большим подавлением нежелательных высокочастотных компонент. Сегодня расчет и создание таких цифровых фильтров, к тому же не вносящих никаких фазовых искажений, не представляют больших трудностей.

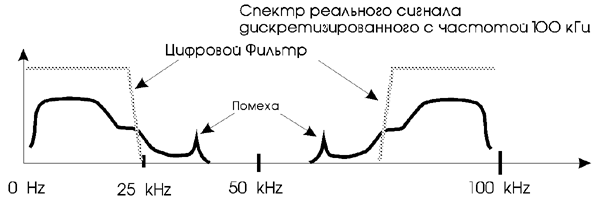
После цифрового фильтра получается цифровое представление сигнала, имеющего спектр, правильно ограниченный по частоте. Применяя к такому сигналу теорему Котельникова мы можем резко понизить частоту его дискретизации до удвоенной величины наивысшей полезной частотной составляющей, чего мы и хотели добиться. Надо отметить, что часто цифровые фильтры находятся в той же микросхеме, что и другие узлы АЦП, так что пользователь даже может и не подозревать какие сложные процессы происходят в его АЦП.

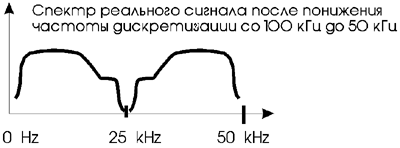
Применяется дискретизация на повышенной частоте (oversampling) и в цифро-аналоговых преобразователях (ЦАП). В ЦАП также есть проблема сложности аналоговых восстанавливающих (интерполирующих) фильтров. Ведь сразу после ЦАП сигнал представляет собой серию дискретных импульсов, имеющих многочисленные алиазинговые спектральные компоненты. На аналоговый фильтр в этом случае возлагается задача полностью пропустить сигнал нужного частотного диапазона (скажем 0..24 кГц) и, по возможности, наиболее полно подавить ненужные высокочастотные компоненты. И, конечно, чисто аналоговому фильтру выполнить такие противоречивые требования очень сложно. Поэтому сначала цифровой сигнал интерполируют, то есть вставляют дополнительные отсчеты, вычисленные по специальным алгоритмам и, тем самым, резко увеличивают частоту дискретизации. Это приводит к тому, что алиазинговые спектральные компоненты на выходе ЦАП далеко отстоят от частотных компонент основного сигнала и, соответственно, чтобы отфильтровать (подавить) их достаточно применить простой аналоговый фильтр.

Не нашли то, что искали? Воспользуйтесь поиском:

Лучшие изречения: Как то на паре, один преподаватель сказал, когда лекция заканчивалась — это был конец пары: "Что-то тут концом пахнет". 8526 — | 8113 — или читать все.

На рисунке 1 приведены основные требования к устройствам дискретизации аналогового сигнала. Дискретизация непрерывных аналоговых данных должна осуществляться с интервалом времени t_д = 1/f_д. При разработке цифрового устройства этот период должен тщательно выбираться для реализации точного представления первоначального аналогового сигнала в цифровой форме.

КРИТЕРИИ ДИСКРЕТИЗАЦИИ ПО КОТЕЛЬНИКОВУ

• Частота дискретизации f_д сигнала с шириной полосы f_в должна удовлетворять условию f_д > 2f_в, в противном случае информация о сигнале будет потеряна
• Эффект наложения спектров возникает, когда f_д

Очевидно, что чем больше будет взято отсчетов аналогового сигнала на интервале времени (больше выбранная частота дискретизации), тем более точным будет представление этого сигнала в цифровом виде. При уменьшении количества отсчетов в единицу времени (уменьшении частоты дискретизации) можно достигнуть предела, после которого преобразованный в цифровую форму сигнал будет искажен до такой степени, что будет невозможно восстановить его в первоначальном виде.

Иными словами, в соответствии с теоремой Котельникова требуется, чтобы частота дискретизации аналогового сигнала была, по крайней мере, вдвое больше полосы полезного сигнала, иначе информация об исходном виде аналогового сигнала будет потеряна. Если выбрать частоту дискретизации меньше (а в большинстве практических устройства и равной) удвоенной полосы частот преобразуемого аналогового сигнала, то возникает эффект, известный как наложение (заворот) спектра (aliasing).

Обычно анализ аналоговых цепей производится при помощи синусоидального сигнала. На нем проще понять физический смысл явлений, возникающих в исследуемом блоке. Так как дискретизатор является аналоговым устройством, то воспользуемся этим методом и мы. Для понимания физического смысла наложения спектра, рассмотрим эффекты, возникающие при дискретизации синусоидального сигнала. Эти эффекты мы проанализируем, как во временном, так и в частотном представлении исследуемого сигнала.

В качестве примера, иллюстрирующего эффект наложения спектра (заворота спектра), на рисунке 2 приведена временная диаграмма синусоидального сигнала, дискретизированного по времени идеальным дискретизатором.

Рисунок 2. Влияние стробоскопического эффекта во временной области, приводящее к наложению спектров входного сигнала

В приведенном на этом рисунке примере, частота дискретизации f_д выбрана лишь ненамного выше частоты входного аналогового сигнала f_в. То есть мы нарушили теорему Котельникова! Обратите внимание, что в результате дискретизации, мы получили отсчеты сигнала, частота которого равна разности частот дискретизации и исходного сигнала f_д – f_a. То есть мы наблюдаем низкочастотный образ реального сигнала. Этот эффект известен в технике как стробоскопический эффект.

На рисунке 3 приведено частотное представление той же самой ситуации. На этом рисунке четко видно, что на выходе идеального дискретизатора появляется не только низкочастотная составляющая с частотой f_д – f_a, но и f_д + f_a, 2×f_д – f_a, 2×f_д + f_a и т.д.

Теперь рассмотрим дискретизацию одиночного синусоидального сигнала с частотой fa идеальным дискретизатором с частотой следования стробирующих импульсов f_д. Пусть, f_д > 2f_a. В частотном спектре на выходе дискретизатора появляются гармоники частоты дискретизации f_д, промодулированные исходным сигналом, в результате чего появляются образы входного сигнала на частотах, равных |±Kf_д ± f_a|, где K = 1, 2, 3, 4, . Эта ситуация отчетливо видна на спектре сигнала полученного с выхода идеального дискретизатора, приведенном на рисунке 3.

Рисунок 3. Спектр дискретизированного аналогового сигнала

Полоса сигнала по Котельникову определяется как спектр от постоянного тока до f_д/2. Частотный спектр на входе дискретизатора разделяется на бесконечное число зон. Полоса частот каждой зоны составляет 0,5f_д. На практике, идеальный дискретизатор перемещает все высокочастотные образы сигнала в полосу частот от 0 до f_д/2, и накладывает их на сигнал, присутствующий в первой зоне частот Котельникова.

Теперь рассмотрим случай, когда частота полезного сигнала выходит за пределы первой зоны Котельникова. При частоте сигнала, немного ниже частоты дискретизации, временная диаграмма приведена на рисунке 2. Этот случай тоже можно проиллюстрировать рисунком 3, однако на этот раз в качестве входного сигнала следует рассматривать сигнал во второй зоне Котельникова, а компонента сигнала в первой зоне возникает после процесса дискретизации.

Обратите внимание, что, несмотря на то, что сигнал находится вне первой зоны Найквиста, его продукт преобразования f_д – f_a попадает внутрь этой зоны. Возвращаясь к рисунку 3, становится ясно, что, если мешающий сигнал появляется на любом из образов частоты f_a, то он тут же переносится на частоту f_a, приводя, таким образом, к появлению мешающего частотного компонента в первой зоне Котельникова.

Такой процесс подобен работе аналогового смесителя. Это означает, что перед устройством дискретизации сигнала обязательно требуется аналоговая фильтрация, подавляющая компоненты этого сигнала, частоты которых находятся вне полосы первой зоны Котельникова и после дискретизации попадают в ее пределы. Требования к амплитудно-частотной характеристике аналогового фильтра на входе дискретизатора будут зависеть от того,как близко частота внеполосного сигнала отстоит от f_д/2, а также величиной требуемого подавления. Эти вопросы мы рассмотрим позднее в главе, посвященной фильтрам, предназначенным для устранения эффекта наложения спектров.

Математическое описание дискретного сигнала

В дискретных системах сигналы представляют собой последовательности отсчетов, взятые через равные промежутки времени Δt. Для того, чтобы выделить одиночный момент времени в математическом представлении применяется дельта-функция δ(t). Как известно, эта функция равна нулю на всем протяжении времени и только в нулевой момент времени становится бесконечной. Так как площадь под дельта-функцией равна единице, то при умножении любой функции (в том числе и входного сигнала) на дельта-функцию мы получим значение входного сигнала в нулевой момент времени.

Если нас интересует значение функции в момент времени T, отличающийся от нуля, то дельта-функцию можно записать: . Тогда значение функции входного сигнала x(t) в момент времени T можно выделить следующим образом:

Для выделения функции в определенные моменты времени, взятые с равными интервалами придется использовать уже сумму дельта-функций. Тогда функцию дискретизации D, представляющую собой сумму дельта-импульсов, отстоящих друг от друга на интервал времени Δt можно записать следующим образом:

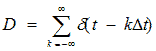(3)

График функции дискретизации приведен на рисунке 1.

Рисунок 1. График функции дискретизации

Теперь для того, чтобы получить дискретизированный сигнал, достаточно умножить функцию дискретизации на исходный непрерывный сигнал x(t). Учитывая, что площать дельта-функции равна единице, в моменты времени, кратные Δt, дискретизированный сигнал будет равен исходному сигналу x(t), а в остальное время дискретизированный сигнал будет равен нулю. В качестве примера на рисунке 2 приведены графики исходного непрерывного сигнала x(t) и дискретизированного сигнала x_д(t).

Рисунок 2. Графики непрерывного и дискретизированного сигналов

Математическое представление дискретного сигнала x_д(t) можно записать в следующем виде:

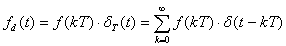(4)

1. Walt Kester "Mixed signal and DSP design techniques" 2000
2. Б. Голд, Ч. Рейдер Цифровая обработка сигналов. пер. с англ., под ред. А. М. Трахтмана. М., "Сов. радио", 1973, 368 с.
3. Ричард Лайонс Цифровая обработка сигналов. — 2-е. — М: Бином-Пресс, 2006. — 656 с.
4. Куприянов М. C. Матюшкин Б. Д. Цифровая обработка сигналов. — 2-е. — СПб: Политехника, 2000. — 592 с.
5. Сергиенко А. Б. Цифровая обработка сигналов. — 2-е. — СПб: Питер, 2006. — 751 с.

Вместе со статьей "Дискретизация сигналов" читают: