Теорема косинусов — теорема евклидовой геометрии, которая обобщающает теорему Пифагора.
Теорема косинусов:
 Для плоского треугольника, у которого стороны a, b, c и угол α, который противолежит стороне a, справедливо соотношение:
Для плоского треугольника, у которого стороны a, b, c и угол α, который противолежит стороне a, справедливо соотношение:
Квадрат стороны треугольника равняется сумме квадратов 2-х других сторон минус удвоенное произведение этих сторон на косинус угла между ними.
Следствие из теоремы косинусов.
- Теорема косинусов используется для определения cos угла треугольника:

h 2 = a 2 — (c – b cos α) 2 (2)
Приравниваем правые части уравнений (1) и (2):
b 2 — (b cos α) 2 = a 2 — (c — b cos α) 2
a 2 = b 2 + c 2 — 2bc cos α.
Если 1-н из углов при основании тупой (высота упирается в продолжение основания), полностью аналогичен рассмотренному выше.
Определить стороны b и c:
Формула теоремы косинусов
Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.
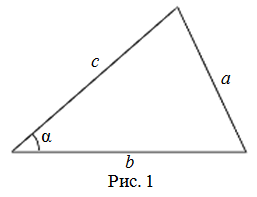
То есть для плоского треугольника (рис. 1) со сторонами $a$, $b$ и $c$ и углом $alpha$, противолежащим стороне $a$, справедливо соотношение:
Теорема косинусов является обобщением теоремы Пифагора. Утверждения, обобщающие теорему Пифагора и эквивалентные теореме косинусов, были сформулированы отдельно для случаев острого и тупого угла в 12 и 13 предложениях II книги "Начал" древнегреческого математика Евклида (ок. 300 г. до н. э.). Утверждения, эквивалентные теореме косинусов для сферического треугольника, применялись в сочинениях математиков стран Средней Азии. Теорему косинусов для сферического треугольника в привычном нам виде сформулировал выдающийся немецкий астролог, астроном и математик Региомонтан (1436 — 1476), назвав её "теоремой Альбатегния" (по имени выдающегося средневекового астронома и математика Абу Абдаллах Мухаммад ибн Джабир ибн Синан ал-Баттани (858 — 929).
В Европе теорему косинусов популяризовал французский математик Франсуа Виет (1540 — 1603) в 16 столетии. В начале 19 века её стали записывать в принятых по сей день алгебраических обозначениях.
Следствие из теоремы косинусов
Теорема косинусов может быть использована для нахождения косинуса угла треугольника (рис. 1):
Если $b^<2>+c^<2>-a^<2>>0$, то угол $alpha$ — острый;
Если $b^<2>+c^<2>-a^<2>=0$, то угол $alpha$ — прямой;
Задание. В треугольнике $ABC AC=3, BC=5$ и $AB = 6 .$ Найти угол, противолежащий стороне $AB$
Решение. Согласно следствию из теоремы косинусов, имеем:
$$angle A C B=arccos left(-frac<1><15>
ight)$$
Ответ. $angle A C B=arccos left(-frac<1><15>
ight)$
Задание. Задан треугольник $ABC$, длины сторон которого $AC=17, BC=14, angle ACB=60^<circ>$. Найти длину третьей стороны рассматриваемого треугольника.
Решение. Согласно теореме косинусов
$$A B^<2>=A C^<2>+B C^<2>-2 cdot A C cdot B C cdot cos angle A C B=$$
$$=17^<2>+14^<2>-2 cdot 17 cdot 14 cdot cos 60^<circ>=289+196-238=24$$

Идёт приём заявок
Подать заявку
Для учеников 1-11 классов и дошкольников


Тема урока: «Теорема косинусов».
Тип урока: урок – семинар.
Цель урока: 1.Сформулировать теорему косинусов, рассмотреть несколько способов
2.Формировать умения применять теоретические знания при решении задач.
3.Повышать интерес к изучению математики.
4.Воспитывать культуру речи, развивать вычислительные навыки.
Технические средства обучения: компьютер, мультимедиа, раздаточный материал (различные способы доказательства).
Методическая литература: учебник «Геометрия 7-9» / Л.С.Атанасян и др.,учебник «Геометрия. 8 класс» /Б.Ф.Бутузов и др./.
Девиз урока: «Кто смолоду делает и думает сам, тот становится потом, надежнее, крепче, умнее. (В.Шукшин).
Объявить цель урока:
Зная зависимость сторон и углов в прямоугольном треугольнике, мы научились находить элементы прямоугольного треугольника. Наша задача состоит в том, чтобы по известным элементам произвольного треугольника, найти другие.
3) Актуализация знаний.
Повторим пройденный материал.

4) Объяснение новой темы:
При проектировании строительства железной дороги на некотором участке, возникла необходимость сооружения тоннеля, сквозь выступ горы между пунктами А и В. Для определения длины тоннеля выбрали на местности некоторый пункт С, из которого видны и доступны пункты А и В.
Чему равна длина тоннеля, если угол С равен 90 0 .

Ответ: АВ= 
Как найти длину тоннеля, если угол С острый.
Пусть 

Решение:
Проведем высоту АН.
Из треугольника АНС находим АН= АС Sin α , АН= 4 Sin 60 0 =  ; СН= АС Cos α ; СН= 4
; СН= АС Cos α ; СН= 4 , ВН= 5-2=3;
, ВН= 5-2=3;
АВ=  , АВ=
, АВ= .
.
На решение задачи будет затрачено меньше времени, если решить задачу с применением теоремы косинусов.
Доказательство ведется несколькими способами.
Доказательство ведут ученики, которые предварительно изучили тему и нашли несколько способов доказательства.
Формулируется теорема косинусов:
Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.


1 способ доказательства. 



Если угол С прямой, тогда Cos C = 0 и формула c 2 = a 2 + b 2 — 2 ab Cos C становится в этом случае теоремой Пифагора. Теорема косинусов является обобщенной теоремой Пифагора.
2 способ доказательства.



3 способ доказательства.




№1. Решают вместе, под руководством учителя, №2-№4 решают по группам (всего 6 групп, по одному одинаковому заданию двум разным группам). Решения проверяются с помощью мультимедиа. Самооценка.











Определите вид ∆ ABC по теореме,
обратной т. Пифагора.


Значит ∆ ABC – прямоугольный, Ð В = 90 0 .
Определим вид ∆ ABC по т. косинусов.















Исторический материал. Сообщение ученика.
Начиная с древних времен и примерно до XVII века в тригонометрии, рассматривали почти исключительно « решение треугольников », т.е. вычисление одних элементов треугольника по другим. Такие вычисления были вызваны запросами астрономии, географии, мореплавания, геодезии и архитектуры. Лишь в XVIII веке в содержании тригонометрии значительно расширяется.
Для решения треугольника, т.е. для нахождения трех его элементов, когда известны другие три его элемента (среди которых, по крайней мере, одна сторона), необходимо иметь три независимых соотношения между шестью его элементами. В евклидовой геометрии одно из них выражается равенством:  .
.
В случае прямоугольного треугольника, помимо т. Пифагора, можно, например, пользоваться соотношениями  .
.
В случае косоугольных треугольников, помимо, можно использовать т. синусов или
Теорема косинусов была по существу доказана, конечно, геометрически, еще в « Началах» Евклида, а именно в 12-м и 13-м предложениях II книги, в которой обобщается т. Пифагора и выводятся формулы, выражающие квадрат стороны, лежащей против острого или тупого угла треугольника. Это положение, доказанное Евклидом, эквивалентно теореме косинусов.
Александрийский математик Герон ( I в), ученые Индии (Брахмагупта, Бхаскара), как и некоторые европейские математики XII — XV в.в. (Л. Фибоначчи), пользовались формулами близкими к формулам т. косинусов, однако, явно была сформулирована (словесно) в XVI в. Французским математиком Ф. Виетом.
Современный вид т. косинусов принимает в 1801 г. у французского математика Лазара Карно (1753г- 1823г).
7) Подведение итогов. Выставление оценок. Рефлексия деятельности на уроке.
Какой способ доказательства наиболее вам понравился и почему?
Выучить тот способ, который наиболее доступен.
Все способы доказательств раздаются ученикам.
